Навигация
Блок преобразования двоичного кода в семисегментный
2.1. Блок преобразования двоичного кода в семисегментный.
Данный блок разрабатывается методом синтеза логических устройств с несколькими выходами, то есть на входе логического устройства есть 4-х значная двоичная комбинация, а на выходе 7-ми значная комбинация (семисегментный код).
Для визуализации чисел требуются индикаторы, отображающие цифры в привычной для человека форме, чаще всего это цифры десятичной и шестнадцатеричной систем счисления.
Простейшим из светодиодных индикаторов, выполняющих функции отображения выше названных чисел и некоторых других символов является семисегментный индикатор. Имеется семь элементов, расположенных так, как показано на рис. 2.1.1.
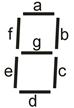
Рис. 2.1.1.
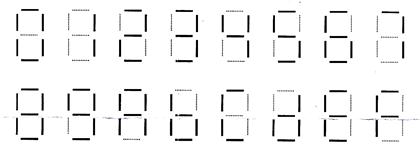 |
Каждый может светиться либо не светиться, в зависимости от значения соответствующей выходной функции, управляющей его свечением. Вызывая свечение элементов в определенных комбинациях, можно получить изображение цифр «0» - «9» и букв «A» – «F» (рис. 2.1.2).
Рис. 2.1.2.
При построении таблицы истинности преобразователя семисегментного кода (табл. 2.1.1) были приняты следующие условия: включенному элементу соответствует сигнал лог.1.
Таблица 2.1.1.Таблица истинности преобразователя семисегментного кода.
| Отображаемые цифры и буквы | Входная комбинация (двоичный код) | Выходная комбинация (семисегментный код) | |||||||||
| X3 | X2 | X1 | X0 | g | f | e | d | c | b | a | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 3 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 7 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| A | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| B | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| C | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| D | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| F | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| G | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
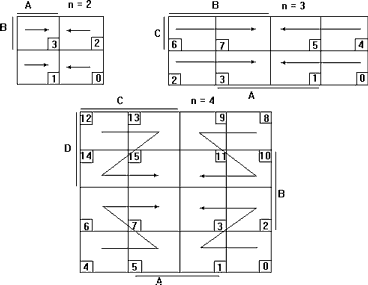
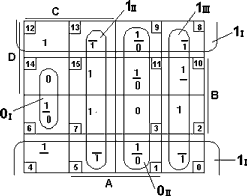
Синтез данного преобразователя производится с помощью минимизации каждой выходной функции в отдельности методом карт Карно.
При минимизации методом карт Карно нужно стремиться, чтобы число областей было минимальным, а каждая область содержала возможно большее число клеток. Т.к. синтезируемое устройство является устройством с несколькими выходами, то для получения минимальной схемы необходимо в картах Карно построить минимальное число областей, обеспечиваемых покрытие клеток, содержащих 1 во всех семи картах.
Для упрощения синтеза и получения минимальной схемы уменьшаем число единиц в картах Карно и, соответственно увеличиваем число «общих» областей. Для этого инвертируем выходные функции в таблице истинности преобразователя семисегментного кода (табл. 2.1.2).
Таблица 2.1.2.
Таблица истинности преобразователя семисегментного кода с инверсными выходами.
| Отображаемые цифры и буквы | Входная комбинация (двоичный код) | Выходная комбинация (семисегментный код) | |||||||||
| X3 | X2 | X1 | X0 |
|
|
|
|
|
|
| |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 5 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| A | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| B | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| C | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| D | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| F | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| G | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
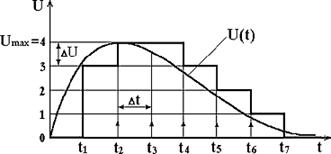
Проанализируем работу преобразователя с помощью временных диаграмм, представленных на рис. 2.1.3.
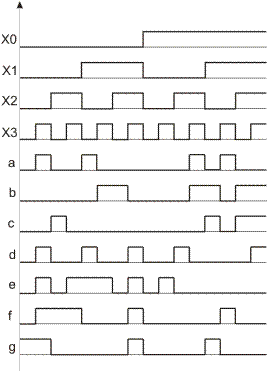
Рис. 2.1.3.
Производим минимизацию каждой выходной функции отдельно методом карт Карно в зависимости от входной комбинации.
Карта Карно для функции ![]() :
:
|
| |||||
| X0
X0 | 0 | 1 | 0 | 1 | X3 X3 X3 |
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 1 | ||
| X2 X2 X2 | |||||
После выделения областей получим следующую функцию ![]()
Карта Карно для функции ![]() :
:
|
| |||||
| X0
X0 | 1 | 1 | 0 | 1 | X3 X3 X3 |
| 0 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | ||
| X2 X2 X2 | |||||
После выделения областей получим следующую функцию ![]()
Карта Карно для функции ![]() :
:
|
| |||||
| X0
X0 | 1 | 1 | 1 | 1 | X3 X3 X3 |
| 0 | 0 | 0 | 1 | ||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| X2 X2 X2 | |||||
После выделения областей получим следующую функцию ![]()
Карта Карно для функции ![]() :
:
|
| |||||
| X0
X0 | 0 | 1 | 0 | 1 | X3 X3 X3 |
| 0 | 1 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| X2 X2 X2 | |||||
После выделения областей получим следующую функцию ![]()
Карта Карно для функции ![]() :
:
|
| |||||
| X0
X0 | 0 | 0 | 0 | 0 | X3 X3 X3 |
| 0 | 1 | 0 | 0 | ||
| 0 | 1 | 1 | 0 | ||
| 1 | 0 | 0 | 0 | ||
| X2 X2 X2 | |||||
После выделения областей получим следующую функцию ![]()
Карта Карно для функции ![]() :
:
|
| |||||
| X0
X0 | 0 | 0 | 0 | 0 | X3 X3 X3 |
| 1 | 1 | 0 | 0 | ||
| 0 | 1 | 1 | 0 | ||
| 0 | 1 | 0 | 0 | ||
| X2 X2 X2 | |||||
После выделения областей получим следующую функцию ![]()
Карта Карно для функции ![]() :
:
|
| |||||
| X0
X0 | 0 | 0 | 0 | 0 | X3 X3 X3 |
| 1 | 0 | 1 | 0 | ||
| 0 | 0 | 0 | 0 | ||
| 0 | 0 | 1 | 0 | ||
| X2 X2 X2 | |||||
После выделения областей получим следующую функцию ![]()
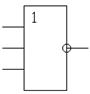
После реализации всех функций можно проследить какие логические элементы участвуют в реализации блока преобразования двоичного кода в семисегментный. Для преобразования двоичного кода в семисегментный потребуются четыре элемента НЕ, трех и четырех-входовые элементы И, трех-, четырех-, пяти-входовые элементы ИЛИ-НЕ.
Таблицы истинности и условно-графические обозначения этих элементов представлены на рис. 2.1.6, где Xi – входные сигналы, Y – выходной сигнал.
| Xi |
|
| 0 | 1 |
| 1 |
|
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
а)
б)
| X1 | X2 | X3 | X4 | Y |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
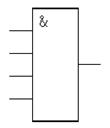
г)
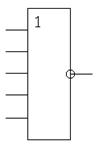
| X1 | X2 | X3 | X4 | X5 | Y |
| 0 | 0 | 0 | 0 | 0 | 1 |
| * | * | * | * | * | 0 |
в)
д)
| X1 | X2 | X3 | X4 | Y |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 |
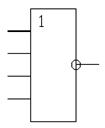
е)
Рис. 2.1.6. – Таблица истинности и УГО элемента: а) НЕ; б) 3И; в) 4И; г) 3ИЛИ-НЕ; д) 5ИЛИ-НЕ; е) 4ИЛИ-НЕ.
Похожие работы
... . Они используются довольно редко, так как применение двоично-десятичных кодов ограничено узкой областью, например, они применяются в схемах многоразрядной десятичной индикации. Примером преобразователя двоичного кода от 0 до 255 в двоично-десятичный код может служить микросхема DM74185A производства фирмы Texas Instruments. 3.3 Семисегментный индикатор с дешифратором Для отображения ...
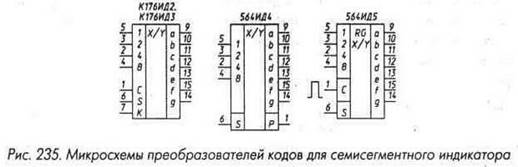
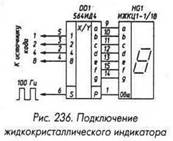
... отношении не являются комбинационными микросхемы К176ИД2, К176ИДЗ и 564ИД5, содержащие регистры хранения информации, но их удобно рассматривать в этом разделе как наиболее близкие к дешифраторам и преобразователям кода. Микросхема 564ИК2 предназначена для управления пятиразрядным полупроводниковым семисегментным индикатором или пятью отдельными индикаторами в динамическом режиме. Она содержит ...
... образом, чтобы число одинаковых склеек было возможно большим. При этом преобразователь кодов будет реализован с меньшим числом ЛЭ. Переменные для входа дешифратора и преобразователя кодов брать с выходов счетчика. В качестве инверторов для адресных переменных применить ЛЭ 2И-НЕ с номером 5 и 6. Для размножения переменных можно использовать входные и выходные гнезда ЛЭ или проводники с ...
... показана на рисунке 8.4 Величина резистора R выбирается из условия [12] 240 Ом < R < 1,5 кОм.(8.5) Рисунок 8.4 Период генерируемых импульсов (8.6) 9. ФУНКЦИОНАЛЬНЫЕ УСТРОЙСТВА КОМПЬЮТЕРНОЙ (ЦИФРОВОЙ) ЭЛЕКТРОНИКИ 9.1 Комбинационные цифровые устройства (КЦУ) Логические устройства, выходные сигналы которых однозначно определяются комбинацией входных логических ...
 X1 X1
X1 X1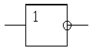 Y
Y 0
0

0 комментариев