3. Экономический смысл последней симплекс -таблицы.
В данной ЗЛП основными переменными симплекс-таблицы являются переменные Х1, Х2, Х3 (продукция), дополнительными Х4, Х5, Х6 (ресурсы).
Кроме того, базисные переменные - Х4, Х3, Х6, небазисные Х1, Х2, Х5.
· При закупке единицы второго ресурса Р2 остаток Р1 уменьшится на 0,83 е.д., производство П3 увеличится на 0,166 шт., а остаток третьего ресурса Р3 снизится на 0,17 станко/час. Анализ основной двойственной переменной (при закупке второго ресурса) показал, что в денежном выражении она составила: 70*0,166 = 11,66 д.е.
· Анализ основных небазисных переменных (не выгодно выпускать х1,х2) показал, что если выпускать одну единицу изделия П1, то остаток Р1 уменьшиться на 1,5 д.е., производство третьего изделия П3 уменьшится на 0,5 шт, а эксплуатация оборудования увеличится на 1,5 станко/час. При этом убыток от этой операции составит в денежном выражении: 70 * 0,5= 35 д.е. абсолютный убыток : 35-30=5 д.е. (=у1); если же выпускать одну единицу изделия П2, то в этом случае остаток первого ресурса Р1 увеличится на 1,17 д.е., выпуск изделия П3 уменьшится на 0,833 шт.,а при использование оборудования уменьшится на 1,83 станко/час. При этом убыток составит 70 * 0,833 = 58,3 д.е., абсолютный убыток: 58,3 - 40 = 18,3 д.е. (=у2).
4. Внутрипроизводственная логистическая система должна гибко реагировать на изменение входящих потоков и цен за единицу выпускаемой продукции, при котором можно использовать полученные оптимальные решения данной задачи.
а) Изменение входящих ресурсных потоков:
D в1 - изменение запаса материала (д.е),
D в2 - изменение количества трудовых ресурсов (чел/час),
D
в3 - изменение фонда рабочего времени оборудования (станко/час).
х4
х5
х6
Новое значение переменных , вошедших в оптимальное решение задачи в базис х3*, х4*, х6*, можно рассчитать как результат перемножения матриц.
| | | | | | | | | | | |
| | | | | | | |
| | | 1 -0,833 0 0 0,166 0 0 -0,83 1 |
| | | | | 1800 + в1 2100 + в2 2400 + в3 |
|
|
|
|
A
-1 = И В*
х4*= 1(1800 + в1) + (-0,833)(2100 + в2) + 0(2400 + в3)

0,
х3*= 0 (1800 + в1) + 0,166(2100 +
в2) + 0 (2400+ в3)  0,
(1)
0,
(1)
х6*= 0(1800 + в1) + (-0,833)(2100 +
в2)+ 1(2400 + в3)  0,
0,
Пусть в2 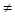 0, в1 и в3 =0, т.е. изменяется количество трудовых ресурсов.
0, в1 и в3 =0, т.е. изменяется количество трудовых ресурсов.
х4*= 1800 - 0,833 в2 - 1743  0,
0,
х3*= 0 + 0,166 в2 + 0 0,
0,
х6*= 0 - 0,833 в2 - 357 + 2400  0,
0,
Выразим в2 и найдем решение неравенств.
| | | | | | | |
| | | | | в2 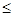 68,67, 68,67, в2  -2100, -2100, в2 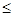 780.3, 780.3, |
|
| |
| | |
|
- 0,833 в2 + 57  0,
0,
0,166 в2 + 348,6  0,
0,
- 0,833 в2 + 2051,4  0,
0,


-2100 68,67 780.3
-2100 < в2 < 68.87 , запас дефицитного ресурса Р2 изменяется в найденном интервале. Если этот запас будет изменятся в этом интервале, то с ассортимент выпускаемой продукции и выручка от реализации тоже будут меняться.
Пусть в1
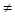
0,
в2 и в3 =0, т.е. изменяется запас материалов, то подставив значения в систему 1 получим следующее:
| | | | | |
| |
| | 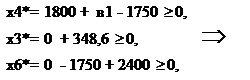 | | | х4*= в1 +50  0, 0, х3*= 348,6 0, 0, х6*= 650  0, 0, |
|
|
Решением неравенства будет следующее : в1 > - 50. Если запас недефицитного ресурса Р1 будет снижаться не больше, чем на 50 д.е., то в оптимальном плане изменяется только неиспользованный остаток первого ресурса. 0
Пусть в3
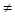
0,
в2 и в1 =0, т.е. изменяется òðåòèé ðåñóðñ, то подставив значения в исходную систему 1 получим следующее:
| х4*= 50  0, 0, х3*= 348,6  0 , 0 , х6*= в3 + 650  0 0 |
|
х4*= 1800 + 1750

,
х3*= 0 + 348,6  0 ,
0 ,
х6*= в3 - 1750 + 2400 0 ,
0 ,
Решением неравенства будет следующее : в3 > - 650. Если запас недефицитного ресурса Р3 будет снижаться не больше, чем на 650 станкочасов., то в оптимальном плане изменяется только неиспользованный остаток третьего ресурса.
б) Изменение цен за единицу выпускаемой продукции (коэффициентов целевой функции С).
| С1* = 30 + С1, С2*= 40 + С2, С3* = 70 + С3, С4* = 0 + С4, С5* = 0 + С5, С6* = 0 + С6, |
|
Пусть С изменяется на С, то получим следующую систему:
| | | |
| | | Тогда -оценки в последней симплекс таблице примут новые значения. Чтобы ранее найденное решение осталось оптимальным, изменение коэффициентов С целевой функции допустимо в таком интервале, для которого - оценки остаются неотрицательными. |
|
|
| |
1 = (0 + С4)1,5 + (70 +
С3)0,5 + (-1,5)(0 + С6) - (30 + С1)  0,
0,
2 = (0 + С4)(-1,17) + (70 + С3)0,833 + 1,833(0 + С6) - (40 + С2)  0,
0,
5 = (0 + С4)(-0,833) + (70 + С3)0,166 + (- 0,833)(0 + С6) - (0 + С5)  0,
0,
Пусть С1
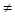
0, а С2= С3= С4= С5= С6=0, то получим:
| | | | | |
| | 1 = 35-30 + С1  0, 0, 2 = 58,31 - 40  0 0 5 = 11,62  0, 0, |
| | | 1 = 5 - С1  0, 0, 2 = 18,31  0 0 5 = 11,62  0, 0, |
|
| | |
|
Решением данного неравенства будет С1 < 5. При цене 4,9 д.е. продукцию П1 производить не выгодно, при уменьшении цены П1 эту продукцию также не выгодно производить, но увеличении цену можно не более, чем на 5 д.е. При этом оптимальный план не изменится.
Пусть С2
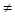
0, а С1= С3= С4= С5= С6=0, то получим:
| 1 = 35-30  0, 0, 2 = 58,31 - 40 + С2  0 0 5 = 11,62  0, 0, |
|
| 1 = 5  0, 0, 2 = 18,31 + С2  0 0 5 = 11,62  0, 0, |
|
Решением данного неравенства будет С2 < 18,31. При цене 18 д.е. продукцию П2 производить не выгодно, при уменьшении цены П2 эту продукцию также не выгодно производить, но увеличении цену можно
не более, чем на 18,31 д.е. При этом оптимальный план не изменится.
Пусть С3
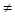
0, а С1= С2= С4= С5= С6=0, то получим:
| С3  -10, -10, С3  -21.98 -21.98 C3  -69,75, -69,75, |
|
| 1 = 35-30 + 0,5 С3  0, 0, 2 = 58,31 - 40 + 0,833 С3 0 0 5 = 11,62 + 0,166 С3  0, 0, |
|

-69.75 -21.98 -10
Решением данного неравенства будет С3 от -10 ло +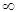 . При изменении цены на продукцию П3 в данном интервале, ассортимент и объемы выпуска продукции не меняются, а выручка от реализации станет другой.
. При изменении цены на продукцию П3 в данном интервале, ассортимент и объемы выпуска продукции не меняются, а выручка от реализации станет другой.
5. В условиях конкуренции стоящая перед предприятием задача меняется, при этом можно использовать следующую оптимальную модель. Условием этой задачи будет являться определение экономического результата, при котором затраты на производство должны быть минимальны нормы расхода на производства одного изделия.
Числовая модель в данном случае будет следующая:
L2 (x) min = 21 x1 + 30 x2 + 56 x3 ,
| | | |
| |
| | | 4x1+ 3x2 + 5x3 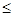 1800 , 1800 , 3x1+ 5x2 + 6x3 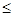 2100 , 2100 , x1+ 6x2 + 5x3 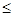 2400 ; 2400 ; 21 x1 + 30 x2 + 56 x3  11025 (45% от L1 max). 11025 (45% от L1 max). |
|
|
x1, x2, x3 > 0
Приведем к каноническому виду данную систему:
L2 (x) min = 21 x1 + 30 x2 + 56 x3 + 0x4 + 0x5 + 0x6 + 0x7,
4x1+ 3x2 + 5x3 + x4= 1800 ,
3x1+ 5x2 + 6x3 + x5= 2100 ,
x1+ 6x2 + 5x3 + x6 = 2400 ;
Раздел:
Логистика Количество знаков с пробелами: 42065
Количество таблиц: 13
Количество изображений: 0
... и наоборот). К такому товару относятся бензины марок АИ-92 и АИ-95, удельный вес которых в товарообороте рос наиболее высокими темпами. 3. Разработка предложений по совершенствованию логистической системы в целях повышения финансовых результатов ЗАО «Рос&Нефть» 3.1 Основные пути улучшения финансовых результатов и финансового состояния фирмы Имущественное положение организации в целом ...
... , энергетических, трудовых ресурсов по отношению к объемным или другим плановым показателям. Комплексный показатель — возврат на инвестиции в логистическую инфраструктуру — характеризует эффективность капиталовложений в подразделения инфраструктуры логистической системы, к которым в настоящее время относят: · складское хозяйство (склады разного вида и назначения, грузовые терминалы и ...
... и т.д., находится в оперативной памяти ЭВМ. В установленные сроки или по запросам информация поступает пользователю и используется для принятия управленческих решений. Информационные логистические системы могут быть созданы на предприятии, охватывать регион, функционировать в рациональном масштабе. Широкое проникновение логистики в сферу управления производством в существенной степени обязано ...
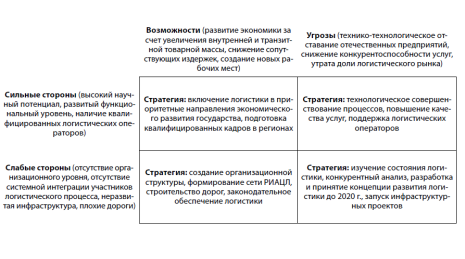
... запасами и закупочную логистику, если закон о госзакупках не позволяет ее использовать? Перспективы развития рынка логистических услуг связаны с системным подходом к макрологистике, опирающейся на тщательно проработанную правовую базу. Резюмируя сказанное, обозначим с позиций классического SWOT-анализа сильные и слабые стороны российской логистики, ее возможности и воздействующие на нее ...
![]() 0,
(1)
0,
(1)![]() 0,
0,![]() 0, в1 и в3 =0, т.е. изменяется количество трудовых ресурсов.
0, в1 и в3 =0, т.е. изменяется количество трудовых ресурсов.![]() 0,
0,![]() 0,
0,![]() 0,
0,![]() 0,
0,![]() 0,
0, ![]() 0,
0, ![]()
![]()
![]() 0 ,
0 ,![]() 0 ,
0 ,![]() 0,
0,![]() 0,
0,![]() 0,
0,![]()
![]() . При изменении цены на продукцию П3 в данном интервале, ассортимент и объемы выпуска продукции не меняются, а выручка от реализации станет другой.
. При изменении цены на продукцию П3 в данном интервале, ассортимент и объемы выпуска продукции не меняются, а выручка от реализации станет другой.


0 комментариев