1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9, 10. ![]()
11, 12. ![]()
13, 14. ![]()
15, 16. ![]()
17. ![]()
18. ![]()
19. ![]()
20. ![]()
21. ![]()
22. ![]()
23. ![]()
24. ![]()
25. ![]()
26. ![]()
27. ![]()
28. ![]()
29. ![]()
30. ![]()
31. ![]()
32. ![]()
33, 34. ![]()
35, 36. ![]()
37. ![]()
38. ![]()
39. ![]()
40. ![]()
41. ![]()
42. ![]()
43. ![]()
44. ![]()
45. ![]()
46. ![]()
47. ![]()
48. ![]()
49. ![]()
50. ![]()
51. ![]()
52. ![]()
53. ![]()
54. ![]()
55. ![]()
56. ![]()
57. ![]()
58. ![]()
59. ![]()
60. ![]()
61. ![]()
62. ![]()
63. ![]()
64. ![]()
65. ![]()
66. ![]()
67. ![]()
68. ![]()
69. ![]()
70. ![]()
71. 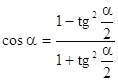
72. 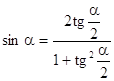
73. 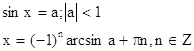
74. ![]()
75. ![]()
76. ![]()
77. 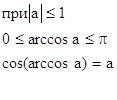
78. 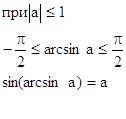
79. 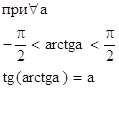
80. 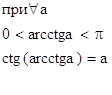
81. ![]()
82. ![]()
83. ![]()
84. 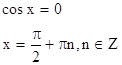
85. 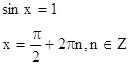
86. ![]()
87. 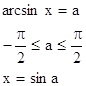
88. 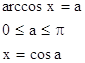
89. 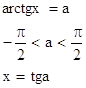
90. 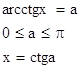
Похожие работы
... сформулированной гипотезы необходимо было решить следующие задачи: 1. Выявить роль тригонометрических уравнений и неравенств при обучении математике; 2. Разработать методику формирования умений решать тригонометрические уравнения и неравенства, направленную на развитие тригонометрических представлений; 3. Экспериментально проверить эффективность разработанной методики. Для решения ...
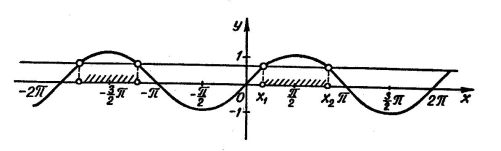
дробно рассмотрено преобразование групп общих решений тригонометрических уравнений. В третьем разделе рассматриваются нестандартные тригонометрические уравнения, решения которых основано на функциональном подходе. В четвертом разделе рассматриваются тригонометрические неравенства. Подробно рассмотрены методы решения элементарных тригонометрических неравенств, как на единичной окружности, так и ...
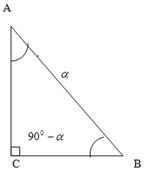
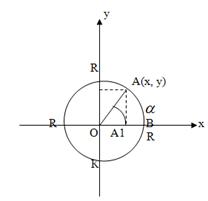
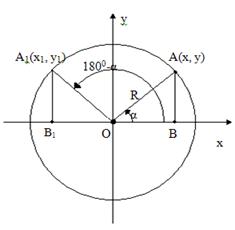
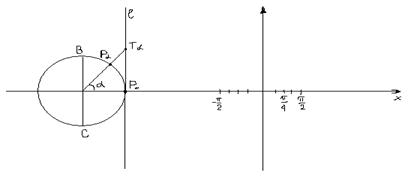
... угол 1800-α= по гипотенузе и острому углу: => OB1=OB; A1B1=AB => x = -x1,y = y1=> Итак, в школьном курсе геометрии понятие тригонометрической функции вводится геометрическими средствами ввиду их большей доступности. Традиционная методическая схема изучения тригонометрических функций такова: 1) вначале определяются тригонометрические функции для острого угла прямоугольного ...
... при помощи которого по данному значению независимой переменной находятся соответствующие ему значения функции. С понятием функции связаны два способа решения уравнений: графический и функциональный. Частным случаем функционального метода является метод функциональной, или универсальной подстановки. Определение. Решить данное уравнение – значит найти множество всех его корней (решений). Множество ...





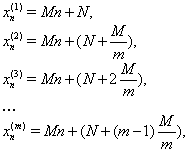
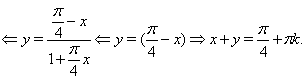

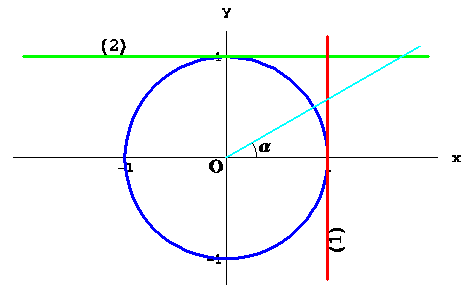
0 комментариев