Итерационные методы решения СЛАУ

1.2 Итерационные методы решения СЛАУ

Метод итераций (метод последовательных приближений).

Приближенные методы решения систем линейных уравнений позволяют получать значения корней системы с заданной точностью в виде предела последовательности некоторых векторов. Процесс построения такой последовательности называется итерационным (повторяющимся).

Эффективность применения приближенных методов зависят от выбора начального вектора и быстроты сходимости процесса.

Рассмотрим метод итераций (метод последовательных приближений). Пусть дана система n линейных уравнений с n неизвестными:

Ах=b, (14)

Предполагая, что диагональные элементы a_ii 0 (i = 2, ..., n), выразим x_i через первое уравнение систем x₂ - через второе уравнение и т. д. В результате получим систему, эквивалентную системе (14):

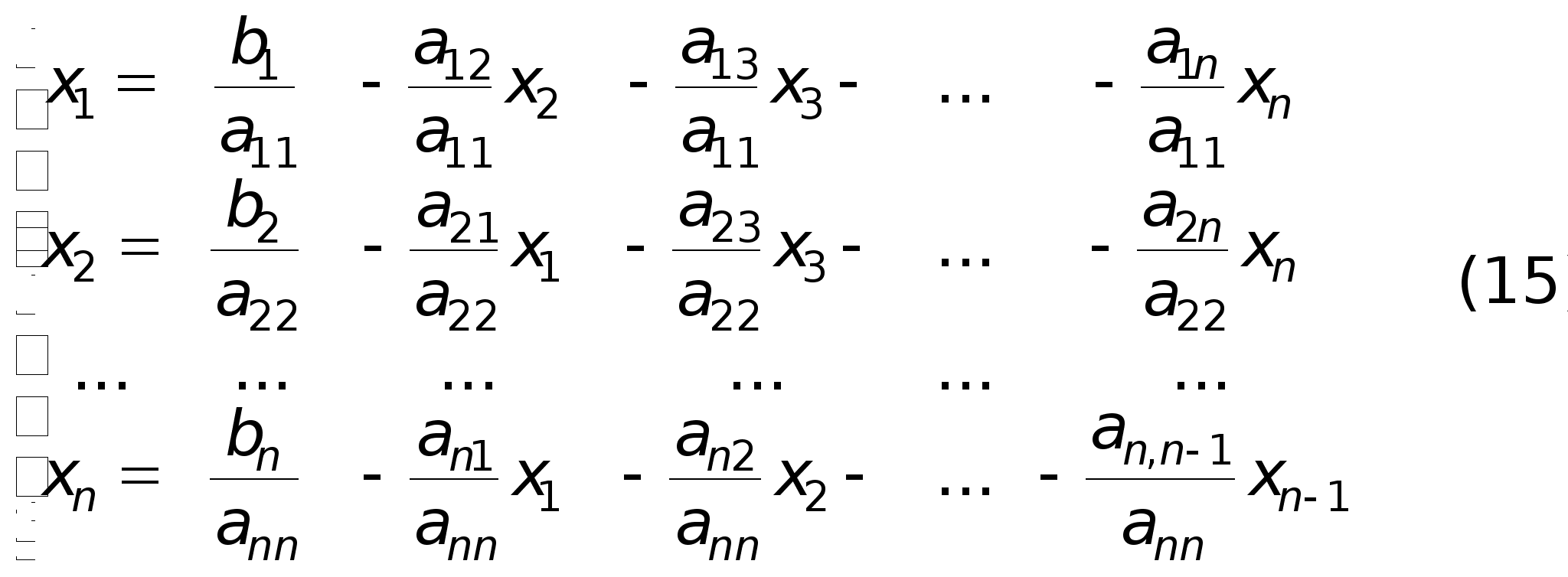
Обозначим ; , где i == 1, 2, ...,n; j == 1,2,..., n. Тогда система (15) запишется таким образом в матричной форме

Решим систему (16) методом последовательных приближений. За нулевое приближение примем столбец свободных членов. Любое (k+1)-е приближение вычисляют по формуле

Если последовательность приближений x(0),...,x(k) имеет предел , то этот предел является решением системы (15), поскольку в силу свойства предела , т.е. [4,6].

Метод Зейделя.

Метод Зейделя представляет собой модификацию метода последовательных приближений. В методе Зейделя при вычислении (k+1)-го приближения неизвестного xi (i>1) учитываются уже найденные ранее (k+1)-е приближения неизвестных xi-1.

Пусть дана линейная система, приведенная к нормальному виду:

(17)

Выбираем произвольно начальные приближения неизвестных и подставляем в первое уравнение системы (17). Полученное первое приближение подставляем во второе уравнение системы и так далее до последнего уравнения. Аналогично строим вторые, третьи и т.д. итерации.

Таким образом, предполагая, что k-е приближения известны, методом Зейделя строим (k+1)-е приближение по следующим формулам:

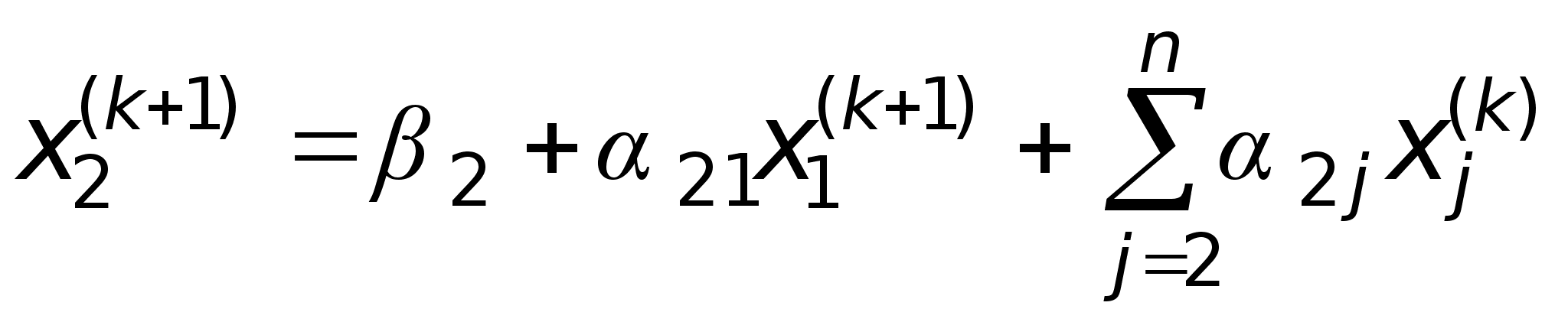
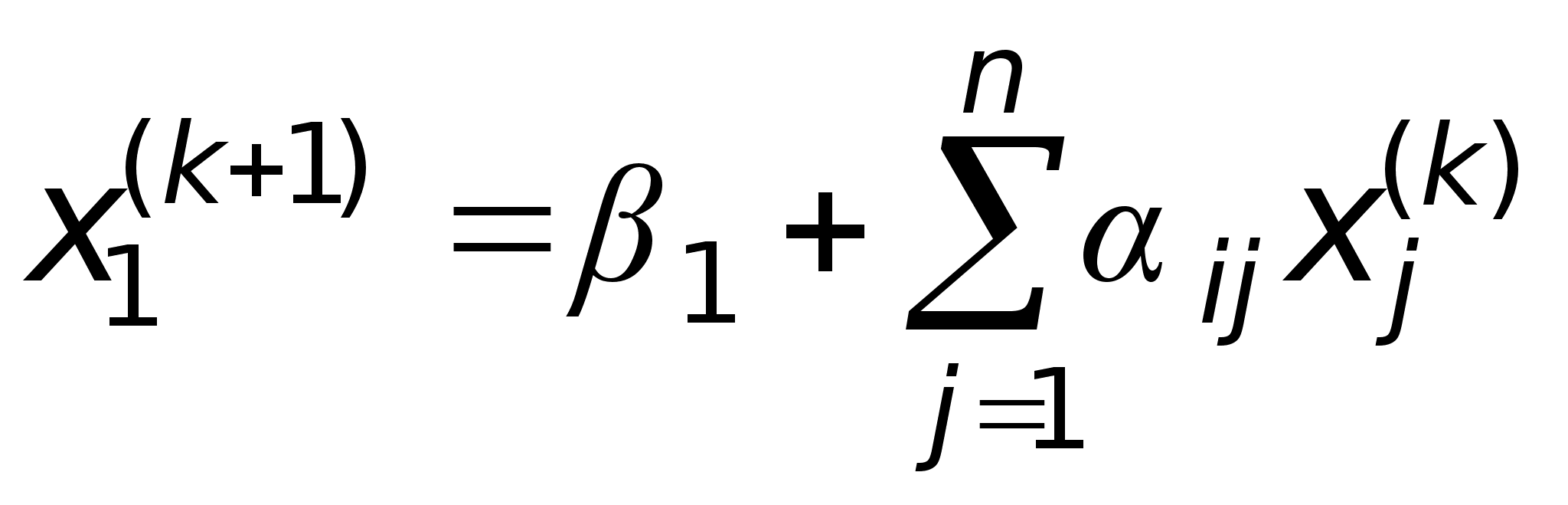
где k=0,1,...,n

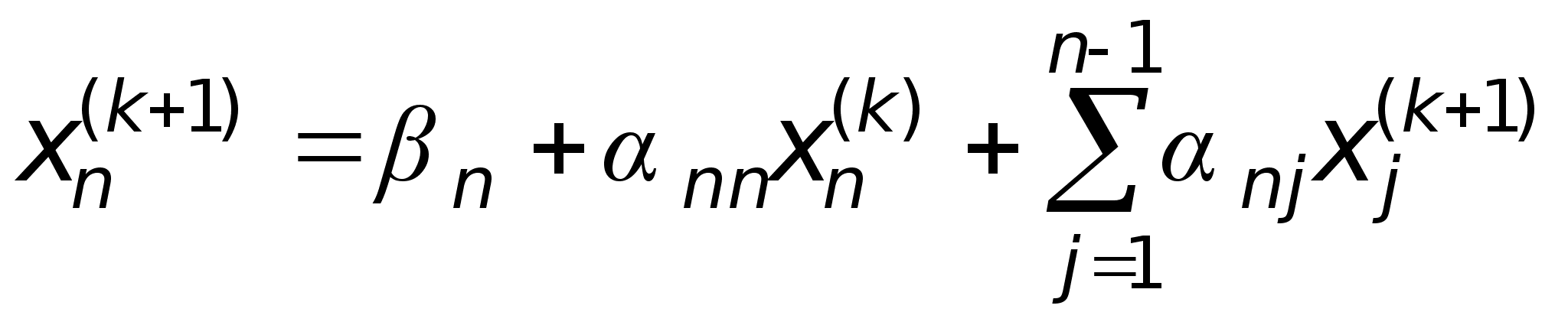
Метод Ланцоша.

Для решения СЛАУ высокого порядка (1), матрица, коэффициентов которой хранится в компактном нижеописанном виде, наиболее удобным итерационным методом является метод Ланцоша [4], схема которого имеет вид:

(18)

где

Преимуществом данного метода является его высокая скорость сходимости к точному решению. Кроме того, доказано, что он обладает свойством «квадратичного окончания», т.е. для положительно определенной матрицы можно гарантировано получить точное решение при количестве итераций . Размер требуемой памяти на каждой итерации не изменяется, т.к. не требует преобразование матрицы . В качестве критерия остановки данного итерационного процесса обычно используют соотношение

, (19)

где - заданная точность. В качестве другого критерия сходимости иногда удобнее использовать среднеквадратичную разность между решениями, полученными на соседних итерациях:

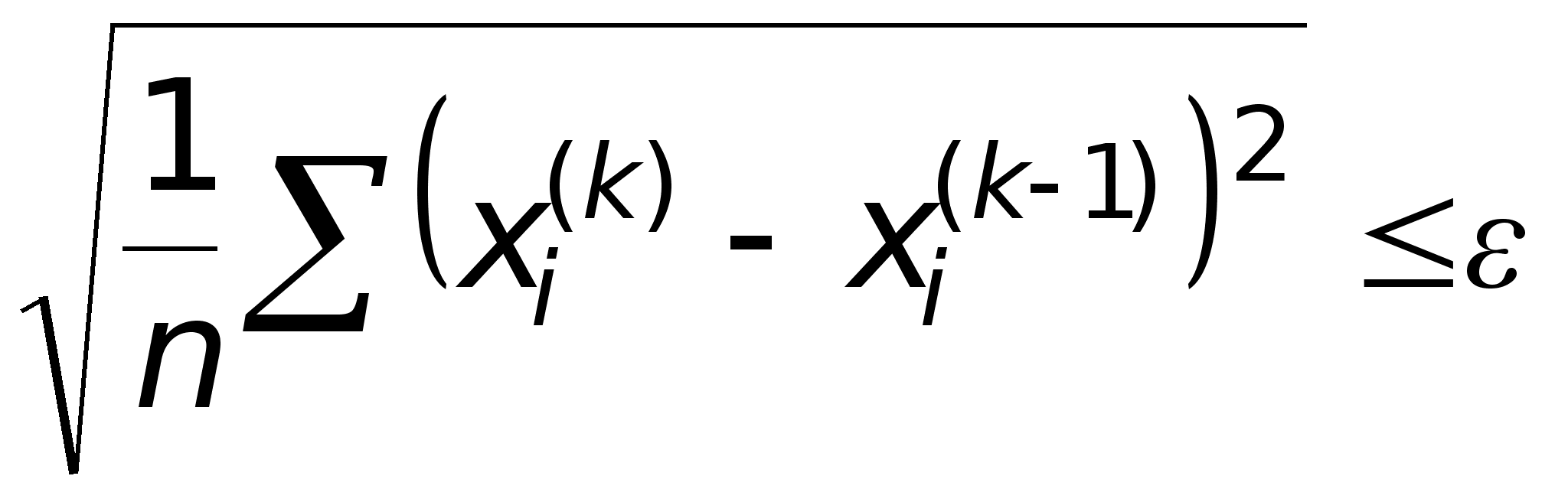(20)

Среднеквадратичную разность необходимо контролировать при выполнении каждых k наперед заданных итераций.

Отдельно следует рассмотреть проблему выбора начального приближения . Доказывается, что при положительно определенной матрице , итерационный процесс (18) всегда сходится при любом выборе начального приближения. При решении контактных задач, когда для уточнения граничных условий в зоне предполагаемого контакта требуется большое количество решений СЛАУ вида (1), в качестве начального приближения для первого расчета используется правая часть системы (1), а для каждого последующего пересчета - решение, полученное на предыдущем. Такая схема позволяет значительно сократить количество итераций, необходимых для достижения заданной точности (19) или (20) [10,11].

Похожие работы

Искусственный интеллект

Скачать

220912

4

1

... и прикладная морфология вновь являются важным полигоном для лингвистичес- кой теории и практики. Обеспечение взаимодействия с ЭВМ на естественном языке (ЕЯ) является важнейшей задачей исследований по искусственному интеллекту (ИИ). Базы данных, пакеты прикладных программ и экспертные системы, основанные на ИИ, требуют оснащения их гибким интерфейсом для многочисленных пользователей, не желающих ...

Свойства информации. Единицы измерения количества информации

Скачать

225314

2

0

... раза. В силу специфичности информации схемы определения количества информа­ции, связанные с ее содержательной стороной, оказы­ваются не универсальными. Универсальным оказывается алфавитный подход к измерению количества информации. В этом подходе сообщение, представленное в какой-либо знаковой системе, рассматривается как совокупность сообще­ний о том, что заданная позиция в последовательнос­ти ...