Вычисление площади сложной фигуры методом имитационного моделирования

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ЭЛЕКТРОННОЙ ТЕХНИКИ

(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)

Расчет площади сложной фигуры с помощью метода

имитацеонного моделирования .

Логвиненко В.

Москва. 1995 г.

Задание: Разработать программу, позволяющую с помощью метода имитационного моделирования рассчитать площадь сложной фигуры, ограниченной сверху кривой U=Y1(x) , снизу V=Y2(x).

1. Для решения данной задачи применим следующий метод.

Ограничим заданную фигуру прямоугольником, стороны которого проходят:

через точки максимального и минимального значения функций и параллельны осям абсцисс;

через левую и правую граничные точки области определения аргумента и параллельны осям ординат.

Используя датчик случайных чисел разыгрываются координаты случайной точки из этого прямоугольника . Проверяем попадаете точки в заданную фигуру. Зная площадь прямоугольника и отношение попавших точек к их общему числу разыгранных, можно оценить площадь интересующей нас фигуры.

2. Технические характеристики объекта исследования:

2.1. Диапазон значений параметров задачи.

Множество кривых ограничим полиномами третьего порядка, в виду того что полиномы более высокого порядка сильно увеличивают время вычисления. Причем для наглядности решения вполне достаточно порядка "3".

Коэффициенты полинома ограничим диапазоном [-100,100] .

Область определения ограничим диапазоном [-100,100].

Эти ограничения введены для более наглядного решения задачи, и изменить их не с технической точки зрения не сложно.

3. Решение задачи.

Данная задача решена в среде Turbo C. Для решения потребовалось общую задачу разбить на несколько небольших задач (процедур).

А именно отдельно( в виде процедур) были решены задачи

-ввод параметров; |

процедура get_poly |

|

-сообщение об ошибке при вводе; | Файл WINDOW.C

процедура talkerror |

|

-рисование рамки окна; |

процедура border |

-вычисление минимального и |

максимального значении функций ; |

процедура f_max |

|

-вычисление значения полинома в |

заданной точке; | Файл MATIM.C

процедура fun |

|

-вычисление корней кубичного |

уравнения; |

процедура f_root |

-вычисление интеграла численным |

методом; |

процедура i_num |

| Файл F_INTEGER.C

-вычисление интеграла с помощью |

имитационного моделирования; |

процедура i_rand |

-инициализация графического режима |

процедура init |

|

-обводка непрерывного контура | Файл DRAFT.C

процедура f_draft |

|

- вырисовка осей координат |

процедура osi |

-вырисовки графиков функций и | Файл DRAFT_F.C

штриховка заданной площади |

процедура draft_f |

-вырисовка графиков вычисления |

площади разными методами и вывод | Файл DRAFT_N.C

таблицы результатов вычисления |

процедура draft_n |

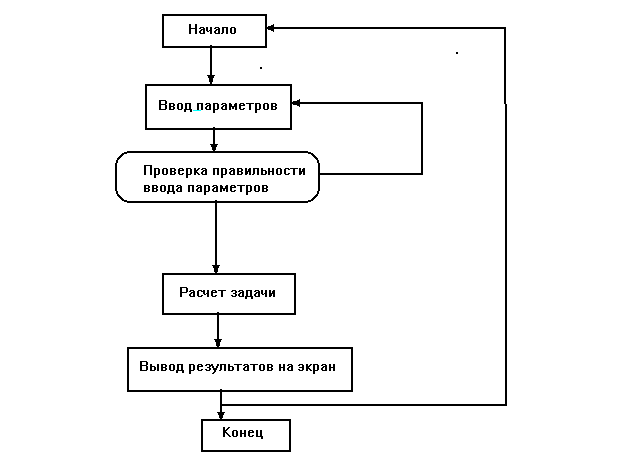
Схема алгоритма имеет вид:

µ §

4. Описание процедур используемый в программе.

4.1 Файл WINDOW.C.

4.1.1 Процедура ввода параметров.

void get_poly( float *b3,float *b2,float *b1,float *b0, //-коэффициенты полинома Y1

fliat *c3,float *c2,float *c1,float *c0, //-коэффициенты полинома Y2

float *x1,float *x2, // область определения [x1,x2]

int *N ) // количество обращений к генератору //случайных чисел

4.1.2 Процедура рисования рамки окна.

void border(int sx, int sy, int en, int ey) // рисует рамку с координатами левого верхнего // угла (sx,sy) и координатами правого нижнего // угла (ex,ey)

4.1.3 Процедура сообщения об ошибке при вводе.

void talkerror(void) -

Процедура подает звуковой сигнал и выводит на экран сообщение об ошибке при вводе.

4.2. Файл MATIM.C

4.2.1 Процедура вычисления максимального и минимального значений функций на заданном интервале.

void f_max(float b3,float b2,float b1,float b0, //-коэффициенты полинома Y1

fliat c3,float c2,float c1,float c0, //-коэффициенты полинома Y2

float x1,float x2, // область определения [x1,x2]

float *amin, float *amax) // минимальное и максимальное значения // функций

4.2.2 Процедура вычисления значения полинома в данной точке.

float fun(float b3,float b2,float b1,float b0, //-коэффициенты полинома

float x)

Возвращает значение полинома в точке х.

4.2.3 Процедура вычисления корней кубичного уравнения.

int f_root(float b3,float b2,float b1,float b0, //-коэффициенты полинома Y1

fliat c3,float c2,float c1,float c0, //-коэффициенты полинома Y2

float x1,float x2, // область определения [x1,x2]

float e, // точность вычисления корней

float *k1,float *k2,float *k3) // значения корней // функций

Возвращает количество действительных корней на данном интервале.

4.3. Файл F_INTEGER.C

4.3.1 Процедура вычисления площади сложной фигуры численным методом.

float f_num(float b3,float b2,float b1,float b0, //-коэфициенты полинома Y1

fliat c3,float c2,float c1,float c0, //-коэфициенты полинома Y2

float x1,float x2) // область определения [x1,x2]

Вычисляет площадь сложной фигуры.

4.3.2 Процедура вычисления площади сложной фигуры c помощью метода имитационного моделрования

float f_(float b3,float b2,float b1,float b0, //-коэфициенты полинома Y1

fliat c3,float c2,float c1,float c0, //-коэфициенты полинома Y2

float x1,float x2, // область определения [x1,x2]

float fmin,float fmax, // минимальное и максимальное значения //функций на данном интервале

int n) // количество обращений к генератору // случайный чисел

Вычисляет площадь сложной фигуры с помощью метода имитационного моделирования.

4.4 Файл DRAFT.C

4.4.1 Процедура инициализации графического режима.

void init (void)

4.4.2 Процедура обводки непрерывного контура.

void f_draft (float b0,float b1,float b2,float b3, //-коэфициенты полинома

float x1,float x2) // область определения [x1,x2]

4.4.3 Процедура вырисовки осей координат.

void osi ( float x1, float x2, // область определения функций

float b) // маштабный коэфициент расчитывается по формуле

// b= j - Fmin*(i-j) / (Fmax - Fmin)

// где i,j - задают положение графика на экране

// Fmin,Fmax - минимальное и максимальное значения //функций на данном интервале

4.5 Файл DRAFT_F.

4.5.1 Процедура вырисовки графиков функций.

void draft_f (float b3,float b2,float b1,float b0, //-коэфициенты полинома Y1

fliat c3,float c2,float c1,float c0, //-коэфициенты полинома Y2

float x1,float x2, // область определения [x1,x2]

float fmin,float fmax, // минимальное и максимальное значения //функций на данном интервале

int k, int i, int l, int j) // координаты, задающие положение //графика на экране

4.6 Файл DRAFT_N.

4.6.1 Процедура вырисовки графиков значений полщадей расчитанных числвым методом и методом имитационного моделирования в зависимости от количества обращений к генератору случайных чисел.

void draft_e (float b3,float b2,float b1,float b0, //-коэфициенты полинома Y1

fliat c3,float c2,float c1,float c0, //-коэфициенты полинома Y2

float x1,float x2, // область определения [x1,x2]

float fmin,float fmax, // минимальное и максимальное значения //функций на данном интервале

float Sn, // площадь рассчитанная числовым методом

int k, int i, int l, int j) // координаты, задающие положение //графика на экране

4.7 Файл SQ.C

Все файлы объединены в главной программе SQ.C, которая является основной и координирует работу процедур.

5 Использование программы.

Для использования данной программы необходима операционная среда MS DOS,

файл egavega.bgi, и собственно сама скомпилированная программа sq.exe.

6 Исходный текст программы дан в приложении №1.

7 Тесовый пример показан в приложении №2.

8 Список использованной литературы.

8.1 Язык программирования Си для персонального компьютера .

С.О. Бочков, Д.М. Субботин.

8.2 С++ . Описание языка программирования.

Бьярн Страустрап.

8.3 TURBO C. User's Guide. Borland International, Inc. 1988.

8.4 TURBO C. Reference Guide. Borland International, Inc. 1988.

9 Заключение.

9.1 Сопоставление результатов работы с тербованием задания.

Сопоставляя результаты работы с требованием задания, можно сказать что задача решена в полной мере, за исключением, быть может общности относительно возможности расчета для многие классов функций. Но решение более общей задачи ( т.е. возможность расчета для многих классов функций ) представляется значительно более громоздким, и вообще является отдельной задачей. Поэтому автор не счел нужным разрабатывать алгоритм ввода многих функций и заострил внимание собственно на самой задаче - расчете площади сложной фигуры с помощью метода имитационного моделирования и сравнение этого метода с числовыми методами.

9.2 Рекомендации по улучшению программы.

При разработке программы автор упустил возможность работы с числовыми массивами. Поэтому, можно улучшить программу переписав ряд процедур под массивы , что сделает программу менее массивной и более наглядной. Широкое

возможности по улучшению программы в области разработки алгоритмов ввода различный классов функций.

Для решения задачи методом имитационного моделирования ограничим данную

§

§

Приложение 1. Текст программы.

Файл sq.c

/*

Пpогpамма SQ основная

*/

#include

#include

#include

#include

#include

#include "matim.c"

#include "window.c"

#include "f_integr.c"

#include "draft.c"

#include "draft_f.c"

#include "draft_e.c"

int k=20,i=15,l=270,j=140;

void main(void)

{

float b0,b1,b2,b3,c0,c1,c2,c3,x1,x2,maxb,maxc,minb,minc,min,max,S;

int N;

do{

closegraph();

get_poly(&b3,&b2,&b1,&b0,&c3,&c2,&c1,&c0,&x1,&x2,&N);

f_max(b3,b2,b1,b0,x1,x2,&minb,&maxb);

f_max(c3,c2,c1,c0,x1,x2,&minc,&maxc);

max=(maxb>maxc)?maxb:maxc;

min=(minb=Fmax)

Fmax=Fx;

if (Fx100) { talkerror(); goto C2; }

C1: gotoxy(k2,k+2); puts("c1= ");

gotoxy(k2+4,k+2); gets(cc1); sscanf(cc1,"%f",&c1);

if (fabs(c1)>100) { talkerror(); goto C1; }

C0: gotoxy(k2,k+3); puts("c0= ");

gotoxy(k2+4,k+3); gets(cc0); sscanf(cc0,"%f",&c0);

if (fabs(c0)>100) { talkerror(); goto C0; }

X1: gotoxy(k1,k+6); puts("x1= ");

gotoxy(k2,k+6); puts("x2= ");

gotoxy(k1+4,k+6); gets(x1c); sscanf(x1c,"%f",&x1);

if (fabs(x1)>100) { talkerror(); goto X1; }

X2: gotoxy(k2,k+6); puts("x2= ");

gotoxy(k2+4,k+6); gets(x2c); sscanf(x2c,"%f",&x2);

if (fabs(x2)>100) { talkerror(); goto X2; }

if (x1>=x2) { talkerror(); goto X1; }

V: R: gotoxy(k1,k+10); puts("QUANTITY OF ADRESSES TO RNG ");

gotoxy(k1+30,k+10); gets(nc); sscanf(nc,"%d",&N);

if (N>32000) { talkerror(); goto R; }

if (N