Тираспольская средняя школа №14
РЕФЕРАТ
на тему:
«Десятичные дроби»
Подготовил:
Тирасполь – 2004 г.
Из истории десятичных и обыкновенных дробей
В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзю-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.
Предшественниками десятичных дробей являлись шестидесятеричные дроби древних вавилонян. Некоторые элементы десятичной дроби встречаются в трудах многих ученых Европы в 12, 13, 14 веках.
Десятичную дробь с помощью цифр и определенных знаков попытался записать арабский математик ал-Уклисиди в X веке. Свои мысли по этому поводу он выразил в "Книге разделов об индийской арифметике".
В XV веке, в Узбекистане, вблизи города Самарканда жил математик и астроном Джемшид Гиясэддин ал-Каши (дата рождения неизвестна). Он наблюдал за движением звезд, планет и Солнца, в этой работе ему необходимы были десятичные дроби. Ал-Каши написал книгу "Ключ к арифметике" (была издана в 1424 году), в которой он показал запись дроби в одну строку числами в десятичной системе и дал правила действия с ними. Ученый пользовался несколькими способами написания дроби: то он применял вертикальную черту, то чернила черного и красного цветов. Но этот труд до европейских ученых своевременно не дошел.
Примерно в это же время математики Европы также пытались найти удобную запись десятичной дроби. В книге "Математический канон" французского математика Ф. Виета (1540-1603) десятичная дробь записана так 2 135436 - дробная часть и подчеркивалась и записывалась выше строки целой части числа.
В 1585 г., независимо от ал-Каши, фламандский ученый Симон Стевин (1548-1620) сделал важное открытие, о чем написал в своей книге "Десятая" (на французском языке "De Thiende, La Disme"). Эта маленькая работа (всего 7 страниц) содержала объяснение записи и правил действий с десятичными дробями. Он писал цифры дробного числа в одну строку с цифрами целого числа, при этом нумеруя их. Например, число 12,761 записывалось так:
1207À6Á1Â12
или число 0,3752 записывалось так:
3752.
Именно Стевина и считают изобретателем десятичных дробей.
Запятая в записи дробей впервые встречается в 1592г., а в 1617г. шотландский математик Джон Непер предложил отделять десятичные знаки от целого числа либо запятой, либо точкой.
Современную запись, т.е. отделение целой части запятой, предложил Кеплер (1571) - (1630 гг.).
В странах, где говорят по-английски (Англия, США, Канада и др.), и сейчас вместо запятой пишут точку, например: 2.3 и читают: два точка три.
Действия над десятичными дробями
1. Сложение (вычитание) десятичных дробей
При сложении (вычитании) десятичных дробей пользуются следующим правилом:
а) уравнивают количество знаков после запятой в обеих дробях (с помощью нулей);
б) записывают дроби друг под другом так, чтобы запятая оказалась под запятой;
в) выполняют действие, не обращая внимания на запятую;
г) подставляют в результате запятую под запятыми в данных дробях
Пример: Сложить 5,607 и 4,1
1. Уравниваем количество знаков после запятой в обеих дробях: 5,607 и 4,100
2. Записываем дроби друг под другом так, чтобы запятая оказалась под запятой:
|
4,100
3,4. Выполняем действие, не обращая внимания на запятую: 9,707
2. Умножение десятичных дробей
2.1. Умножение десятичной дроби на натуральное число
При умножении десятичных дробей на натуральное число используют правило
а) умножают дробь на это число, не обращая внимания на запятую;
б) в полученном произведении отделить запятой столько цифр справа, сколько их отделено в данной дроби
Пример: Умножить 8,607 на 5
1. Умножаем дробь на число, не обращая внимания на запятую:
|
5
![]() 43,035 .
43,035 .
2. В полученном произведении отделяем 3 знака справа: 43,035
2.2. Умножение десятичных дробей
а) выполняют умножение, не обращая внимания на запятые;
б) отделяют запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе
Пример: Умножить 1,25 на 2,04
1. Записываем дроби друг под другом так, чтобы запятая оказалась под запятой:
|
2,04
![]()
|
250 .
![]() 2,5500 .
2,5500 .
2. В полученном произведении отделяем 4 знака справа: 2,5500
3. Деление десятичных дробей
3.1. Деление десятичной дроби на натуральное число
При делении десятичной дроби на натуральное число запятая ставится в частном, когда заканчивают деление целой части.
Если целая часть меньше делителя, то частное начинается с нуля целых
Пример: Разделить 0,644 на 92
|
![]() 0 0,007
0 0,007
|
0
|
0
|
644
![]() 0
0
3.2. Деление десятичной дроби на десятичную дробь
а) в делимом перенести запятую вправо на столько цифр, сколько их после запятой в делителе;
б) после этого выполнить деление на натуральное число
Пример: Разделить 2,808 на 0,12
1. Переносим в числе 2,808 запятую в право на 2 знака, так как у нас в числе 0,12 два знака после запятой, и наша задача сводится к делению 280,8 на 12.
![]()
280,8 12
![]() 24 23,4
24 23,4
![]() 40
40
36
![]() 48
48
48
![]() 0
0
Получаем 280,8 : 12 = 23,4.
Литература
1. Депман И.Я. История арифметики. М.: Просвещение, 1965. 415 с.
2. Свечников А.А. Путешествие в историю математики или Как люди учились считать: Книга для тех, кто учит и учится. М.: Педагогика-Пресс, 1995. 168 с.
Похожие работы
... в переходный период от начальной школы к средней. Глава 2. Методика формирования вычислительных навыков у учащихся 5-го класса при изучении темы «Десятичные дроби» 2. 1. Разработка системы упражнений по формированию устных вычислительных навыков Формирование вычислительных навыков - одна из главных задач, которая должна быть решена в ходе обучения детей в школе. Школа всегда уделяла ...
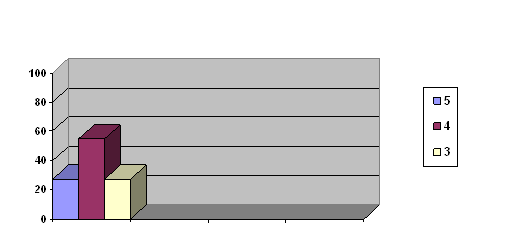
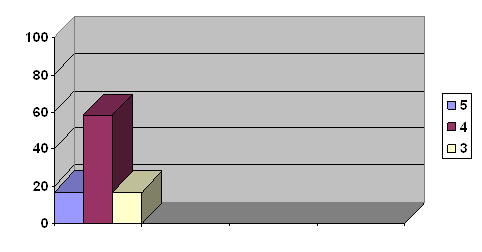
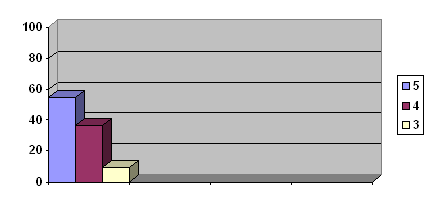
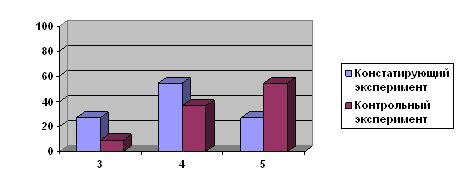
... показал, что на начало эксперимента, качество знаний у учащихся находится на одном уровне. 2. Формирующий эксперимент. Цель: повышение качества знаний учащихся 5 «А» класса при помощи мультимедийного проектора. В экспериментальном - 5 «А» классе проводились уроки с использованием мультимедийного проектора. Они были направлены на повышение качества знаний учащихся. В контрольном – 5 «Б» классе ...
... рациональные числа могут ими разлагаться в бесконечные цепные дроби. Например, имеется разложение =, , , , , … 0,3; 0,42; 0,45; 0,467; … Примечательно то, что квадратические иррациональности разлагаются и в непериодические цепные дроби общего вида. Например, имеется разложение =, , , , , , , … 1; 1,5; 1,38; 1,44; 1,40; … Но самое интересное и важное это то, что в то время как до настоящего ...
... натуральных чисел. Кстати, термин «рациональное число» произошел от латинского слова ratio, что в переводе на русский язык означает «отношение» (частное). 1.3. Содержание темы «Обыкновенные дроби» в школьном курсе математики. Изучение темы «Обыкновенные дроби» в начальной школе. В соответствии с программой по математике, в начальных классах должна быть проведена подготовка к изучению дробей в ...
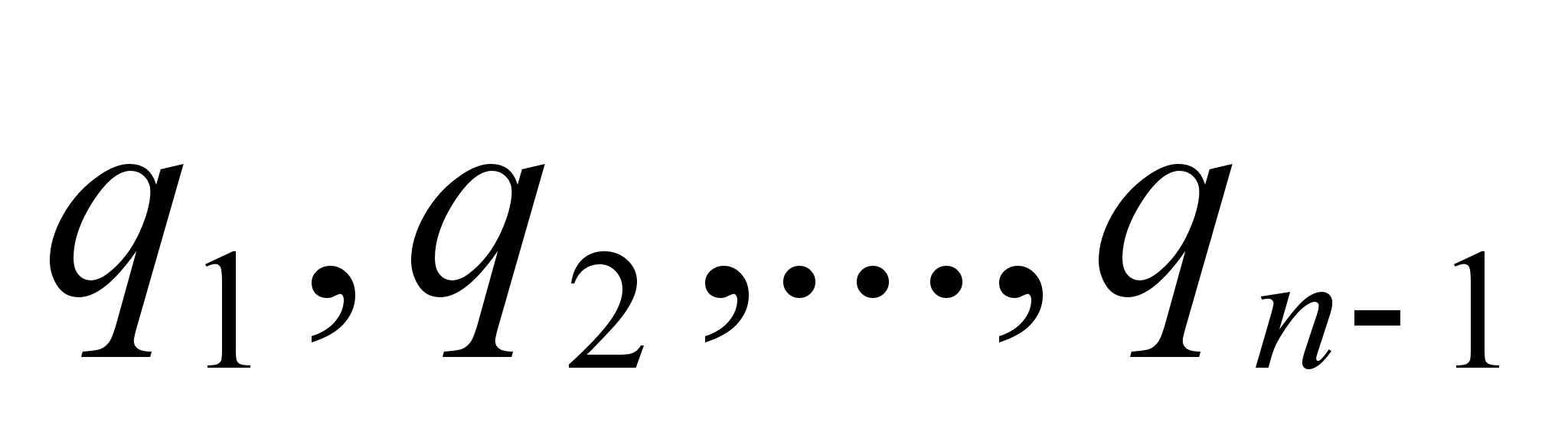
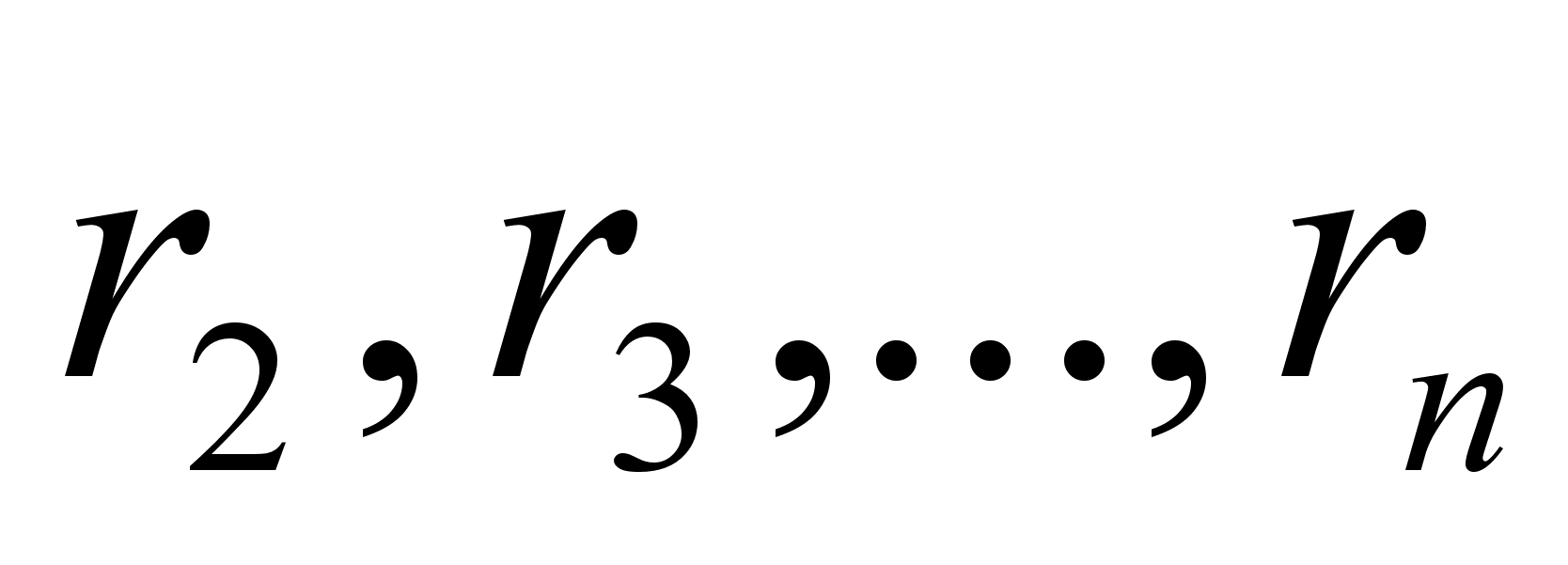
0 комментариев