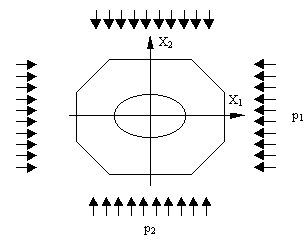
Рассмотрим бесконечную пластинку с некоторым отверстием в центре. Центр отверстия примем за начало координат, а оси х1, х2 направим по главным направлениям упругости. На пластинку действуют некоторые распределенные нагрузки p1, p2 вдоль соответствующих осей.
Общая система уравнение теории упругости выглядит следующим образом:
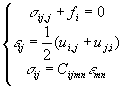 (1)
(1) Уравнения равновесия применительно к рассматриваемой задаче, т.е. когда напряжения зависят только от двух координат, запишутся так:
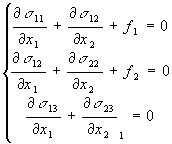 (2)
(2) В нашей задаче искомыми являются шесть функций компонент тензора напряжений ![]() . Но в уравнения равновесия (2) не входит
. Но в уравнения равновесия (2) не входит ![]() , тем самым этой функции определяется особая роль. Для простоты последующих математических выкладок примем следующие предположения. Пусть для f1(x1,x2) и f2(x1,x2) существует потенциал, т.е. такая функция U(x1,x2) для которой выполняются условия:
, тем самым этой функции определяется особая роль. Для простоты последующих математических выкладок примем следующие предположения. Пусть для f1(x1,x2) и f2(x1,x2) существует потенциал, т.е. такая функция U(x1,x2) для которой выполняются условия:
Так как силы f1 и f2 задаются при постановки задачи, то потенциал U так же известная функция. Подставляя (3) в (2) получим:
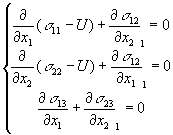 (4)
(4) Введем также еще две функции F(x1,x2) и y (x1,x2), которые называются функциями напряжений и вводятся следующим образом:
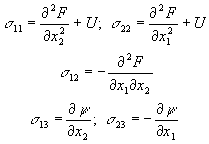
Нетрудно видеть, что при подстановки всех этих формул в систему (4) все три уравнения будут равны нулю. Теперь если мы найдем функции F(x1,x2) и y (x1,x2), то будут найдены и функции компонент тензора напряжений, кроме компоненты ![]() .
.
Для упрощения дальнейших выкладок сделаем следующие преобразования. Так как тензор модулей упругости Сijmn представляет собой матрицу 6х6 из которых 21 компонента независимая, то для тензора напряжений и тензора деформаций вводится матрица столбец:
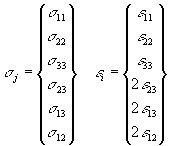
Тогда уравнения Коши запишутся следующим образом:
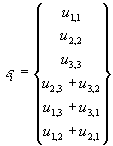
а через напряжения компоненты деформации определяются по закону Гука:
где aij - компоненты матрицы независимых постоянных тензора упругих податливостей Dijmn.
Обозначим ![]() как неизвестную функцию D(x1,x2), тогда из закона Гука следует, что:
как неизвестную функцию D(x1,x2), тогда из закона Гука следует, что:
а выражение для ![]() будет равно:
будет равно:
Теперь введем приведенные коэффициенты деформации![]() , для которых имеет место выражение:
, для которых имеет место выражение:
Подставим выражение для ![]() в обобщенный закон Гука, тогда с учетом приведенных коэффициентов деформаций эти выражения примут вид:
в обобщенный закон Гука, тогда с учетом приведенных коэффициентов деформаций эти выражения примут вид:
Подставляя эти выражения в уравнения Коши получим следующую систему:
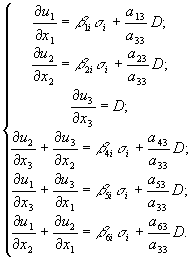 (7)
(7) Уравнения системы (7) включают в себя и уравнения Коши и закон Гука. В этой системе величины ![]() - константы, величины
- константы, величины ![]() и D зависят от двух координат x1 и x2, а перемещения ui - функции трех координат.
и D зависят от двух координат x1 и x2, а перемещения ui - функции трех координат.
Система (7) является системой в частных производных относительно ui и решается последовательным интегрированием уравнений. Интегрирование следует проводить в следующем порядке - сначала необходимо проинтегрировать 3, 4 и 5 уравнения. После интегрирования 3-го уравнения получим:
Подставляя u3 в 4-ое уравнение и интегрируя его получим:
Аналогично с 5-ым уравнением:
Подставляя полученные перемещения в неиспользованные соотношения уравнений Коши, и приравнивая к 0 сомножители при степенях x3, получим:
Исходя из того, что:
функция D будет иметь вид:
Тогда с учетом системы (7) получим:
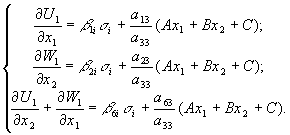 (15)
(15) Исключая V1, U1, W1 ( путем дифференцирования, сложения и вычитания) получим:
Подставляя в уравнения (16) и (17) выведенные нами выражения для напряжений через функции F(x1,x2) и y (x1,x2) и группируя получим:
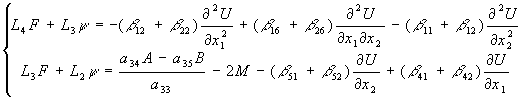 (18)
(18) где L4, L3, L2 - дифференциальные операторы в частных производных 4-го, 3-го и 2-го порядков:
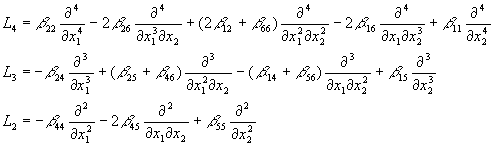
Уравнения (18) представляют собой систему 2-х дифференциальных уравнений в частных производных. Уравнения - линейные, неоднородные, с постоянными коэффициентами.
Общее решение системы (18) для функций напряжения можно представить в виде:
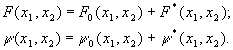
F0 и y 0 - общее решение соответствующей однородной системы:
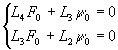 (19)
(19) F* и y * - частные решения неоднородной системы уравнений (18). Частные решения зависят от правых частей уравнений и если эти правые части несложны, то и частные решения обычно описать нетрудно.
Чтобы получить общее решение однородной системы (19) исключим из нее y 0:
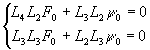 (20)
(20) В силу симметрии L их можно менять местами:
Таким образом, мы получили линейное дифференциальное уравнение 6-го порядка для функции F. Аналогично находим уравнение для y :
Оказалось, что F0 и y 0 должны удовлетворять одинаковым условиям. Оператор 6-го порядка можно разложить на 6-ть линейных операторов 1-ого порядка Dk и уравнение (21) представить в виде:
Из теории диф. уравнений и условия что функция F0 зависит только от x1 и x2 для Dk имеем:
где ![]() - это корни алгебраического (характеристического) уравнения шестой степени, соответствующего дифференциальному уравнению (21).
- это корни алгебраического (характеристического) уравнения шестой степени, соответствующего дифференциальному уравнению (21).
Интегрирование линейного уравнения 6-го порядка можно свести к последовательному интегрированию шести уравнений первого порядка. В результате получим следующие общие выражения:
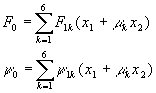
Если среди корней характеристического уравнения есть кратные, задача упрощается, однако решение системы (19) может быть найдено в любом случае исходя из следующих рассуждений.
Любые 6 вещественных чисел можно принять в качестве значений независимых компонент тензора напряжений в данной точке упругого анизотропного тела. Удельная потенциальная энергия деформации есть величина положительная при любых вещественных и не равных нулю значениях компонент тензора напряжений в данной точке. Исходя из этих предположений можно доказать теорему, согласно которой алгебраическое характеристическое уравнение системы (21), не имеет вещественных корней. Поэтому можно утверждать, что числа ![]() в общем решении системы (19), а также в условиях связи всегда комплексные или чисто мнимые.
в общем решении системы (19), а также в условиях связи всегда комплексные или чисто мнимые.
Наряду с комплексными параметрами вводят и систему комплексных переменных:
Введение комплексных переменных позволяет использовать при аналитическом решении рассматриваемой задачи об упругом равновесии анизотропного тела математический аппарат и методы функций комплексных переменных. Эти методы, применительно к данной задаче являются очень эффективными и позволяют получить аналитическое решение многих плоских задач теории упругости анизотропного тела.
2. Прикладная часть 2.1 Физическая постановка задачи.Рассмотрим бесконечную пластинку из ортотропного материала с эллиптическим отверстием в центре. Направление главных осей эллипса совпадает с главными осями упругости материала, усилия приложены на бесконечности вдоль главных осей.
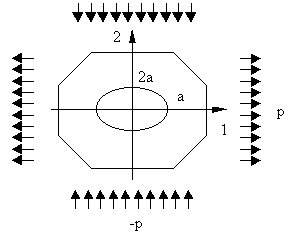
Введем следующие обозначения 2a, 2b - главные оси эллипса, с=a/b, р - усилие на единицу площади. В нашем случае отношение полуосей эллипса с=1/2. Вдоль оси 1 на бесконечности приложено растягивающее усилии р, а вдоль оси 2 - сжимающее -р. Наша задача найти напряжения на краю отверстия и построить их эпюру.
2.2 Упругие свойства материала.Пластинка сделана из стеклопластика C-II-32-50 со следующими характеристиками:
Е1=13,0 ГПа;
Е2=19,8 ГПа;
Е3=7,8 ГПа;
G12=4,05 ГПа;
G13=6,4 ГПа;
G23=3,2 ГПа;
n 13=0.25;
n 32=0.14;
n 12=0.176;
n 23=0.06.
2.3 Математическая постановка задачи.Уравнения равновесия применительно к нашей задаче, когда напряжения зависят только от двух координат и fi=0, запишутся так:
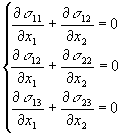
Граничные условия будут иметь следующий вид:
или в развернутом виде применительно к нашей задаче:
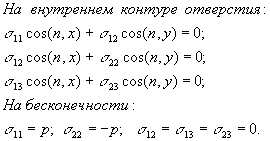
где n - нормаль к контуру отверстия.
2.4 Аналитическое решение.Решая данную задачу по методу изложенному в первой части с учетом того, что материал у нас ортотропный выясняем что характеристическое уравнение для определения коэффициентов ![]() распадается на уравнения 4 и 2 степени:
распадается на уравнения 4 и 2 степени:
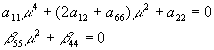
Отсюда немедленно вытекают следующие соотношения:
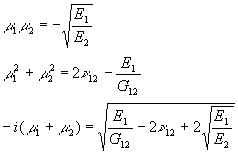
Как мы увидим в дальнейшем этих соотношений достаточно и искать непосредственно ![]() не требуется.
не требуется.
Для решения нашей задачи воспользуемся формулами полученными в работе [1]. Нам надо будет провести только некоторые обобщения и объединение этих формул.
Определим для начала необходимые нам константы аij:
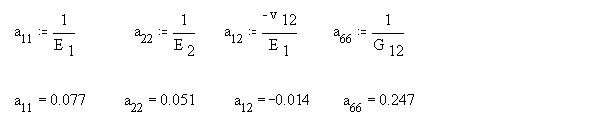 введем теперь следующие обозначения:
введем теперь следующие обозначения: 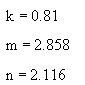
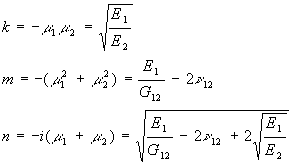
Беря уравнение контура в параметрическом виде, т.е. полагая:
введем еще обозначения для функций, зависящих от параметра ![]() :
:
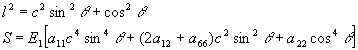
Нас будет интересовать только напряжение у края отверстия - ![]() где, как показывает ряд решенных задач, оно получается наибольшим. Опуская промежуточные выкладки приведем две формулы (при растяжении вдоль большой и малой оси эллипса):
где, как показывает ряд решенных задач, оно получается наибольшим. Опуская промежуточные выкладки приведем две формулы (при растяжении вдоль большой и малой оси эллипса):
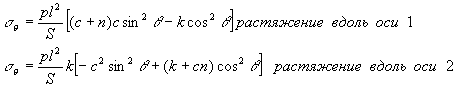
для нашей задачи в силу принципа суперпозиции (а его можно применить, так как мы рассматриваем линейную связь между напряжениями и деформациями, а также считаем их малыми) получим следующую общую формулу:
Для построения эпюры напряжений на краю отверстия воспользуемся возможностями математического пакета MathCad 7.0. Используя найденную нами формулу рассчитаем напряжения ![]() в зависимости от угла и отложим их на графики от контура отверстия на продолжении лучей, проведенных из центра через данные точки контура. Положительные напряжения изображены стрелками направленными от центра к периферии, отрицательные - стрелками направленными к центру. При расчетах полагалось р=1.
в зависимости от угла и отложим их на графики от контура отверстия на продолжении лучей, проведенных из центра через данные точки контура. Положительные напряжения изображены стрелками направленными от центра к периферии, отрицательные - стрелками направленными к центру. При расчетах полагалось р=1.
Результаты расчета и график распределения напряжений приведены соответственно в приложениях 1 и 2.
Проведем небольшой анализ полученных результатов. Как мы видим максимальное напряжение наблюдается в точках ![]() , оно равно
, оно равно
-6р. То есть наблюдаем концентрацию в 6 раз по сравнению с пластинкой без отверстия.
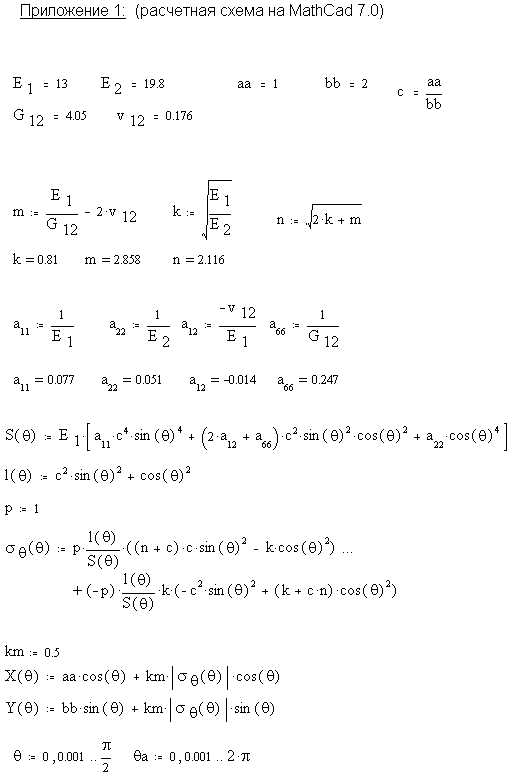 Приложение 2. (График распределения напряжений)
Приложение 2. (График распределения напряжений)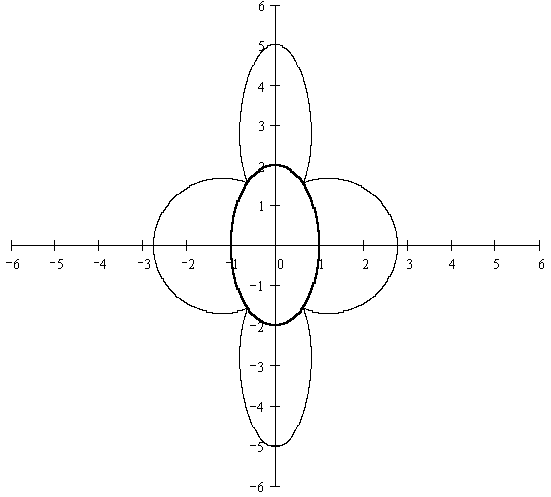
Похожие работы
... и трещинами. Решение построено на использовании теории функции комплексного переменного и удовлетворении граничным условиям методом наименьших квадратов. 1 Термодинамические основы термоупругости 1.1 Термоупругость Основное уравнение термоупругости. При термическом расширении изотропное тело деформируется таким образом, что компоненты деформации отнесенные к системе прямоугольных осей ...
... среды является исключением, а несовпадение — правилом, в связи с чем иногда говорят — с большой долей условности даже о «собственном микроклимате растений». Различают разные экологические типы растений по отношению к температуре. У растений термофильных, или мегатермных (теплолюбивых), оптимум лежит в области повышенных температур. Они обитают в областях тропического и субтропического климата, а ...



0 комментариев