МОУ СОШ «УК №20»
![]()
уравнения и неравенства
реферат по алгебре
ученика 11 «В» класса
Торосяна Левона
Руководитель:
Олейникова Р. М.
Сочи 2002г.
Содержание.
I. Введение
II. Основные правила
III. Иррациональные уравнения:
· Решение иррациональных уравнений стандартного вида.
· Решение иррациональных уравнений смешанного вида.
· Решение сложных иррациональных уравнений.
IV. Иррациональные неравенства:
· Решение иррациональных неравенств стандартного вида.
· Решение нестандартных иррациональных неравенств.
· Решение иррациональных неравенств смешанного вида.
V. Вывод
VI. Список литературы
I. Введение
Я, Торосян Левон, ученик 11 «В» класса, выполнил реферат по теме: «Иррациональные уравнения и неравенства».
Особенностью моей работы является то, что в школьном курсе на решение иррациональных уравнений отводится очень мало времени, а ВУЗовские задания вообще не решаются. Решение иррациональных неравенств в школьном курсе не рассматри- вают, а на вступительных экзаменах эти задания часто дают. Я самостоятельно изучил правила решения иррациональных уравнений и неравенств. В реферате показаны решения как иррациональных уравнений и неравенств стандартного типа, так и повышенной сложности. Поэтому реферат можно использовать как учебное пособие для подготовки в ВУЗ, также рефератом можно пользоваться при изучении этой темы на факультативных занятиях.II. Иррациональные уравнения
Иррациональным называется уравнение, в котором переменная содержится под знаком корня.
Решаются такие уравнения возведением обеих частей в степень. При возведении в четную степень возможно расширение области определения заданного уравнения. Поэтому при решении таких иррациональных уравнений обязательны проверка или нахождение области допустимых значений уравнений. При возведении в нечетную степень обеих частей иррационального уравнения область определения не меняется.
Иррациональные уравнения стандартного вида можно решить пользуясь следующим правилом:
![]()
![]()
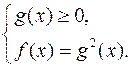
Решение иррациональных уравнений стандартного вида:
а) Решить уравнение ![]() = x – 2,
= x – 2,
Решение.
![]() = x – 2,
= x – 2,
2x – 1 = x2 – 4x + 4, Проверка:
x2 – 6x + 5 = 0, х = 5, ![]() = 5 – 2,
= 5 – 2,
x1 = 5, 3 = 3
x2 = 1 – постор. корень х = 1, ![]()
![]() 1 – 2 ,
1 – 2 ,
Ответ: 5 пост. к. 1 ![]() -1.
-1.
б) Решить уравнение ![]() = х + 4,
= х + 4,
Решение.
![]() = х + 4,
= х + 4,
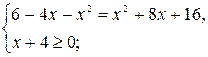
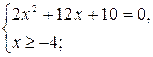
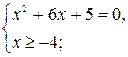
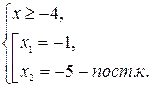
Ответ: -1
в) Решить уравнение х – 1 = ![]()
Решение.
х – 1 = ![]()
х3 – 3х2 + 3х – 1 = х2 – х – 1,
х3 – 4х2 + 4х = 0,
х(х2 – 4х + 4) = 0,
х = 0 или х2 – 4х + 4 = 0,
(х – 2)2 = 0,
х = 2
Ответ: 0; 2.
г) Решить уравнение х – ![]() + 4 = 0,
+ 4 = 0,
Решение.
х – ![]() + 4 = 0,
+ 4 = 0,
х + 4 = ![]() , Проверка:
, Проверка:
х2 + 8х + 16 = 25х – 50, х = 11, 11 – ![]() + 4 = 0,
+ 4 = 0,
х2 – 17х + 66 = 0, 0 = 0
х1 = 11, х = 6, 6 – ![]() + 4 = 0,
+ 4 = 0,
х2 = 6. 0 = 0.
Ответ: 6; 11.
Решение иррациональных уравнений смешанного вида:
· Иррациональные уравнения, содержащие знак модуля:
а) Решить уравнение ![]() =
= ![]()
Решение.
![]() =
= ![]() ,
, ![]() – +
– +
![]() x
x
Учитывая ноль подкоренного выражения, данное уравнение равносильно двум системам:
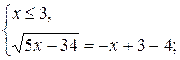
![]() или
или 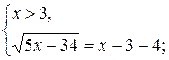
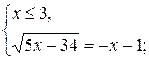
![]()
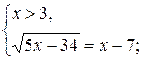
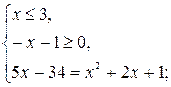
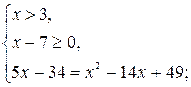
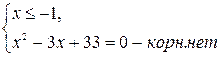
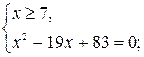
![]()
![]()
![]()
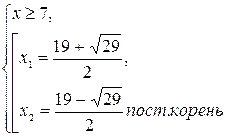
Ответ: ![]()
б) Решить уравнение ![]()
Решение.
![]()
![]() ,
,![]()
![]() – +
– +
x
Учитывая ноль подкоренного выражения, данное уравнение равносильно двум системам:
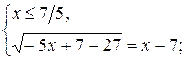 или
или 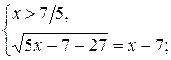
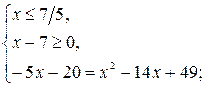
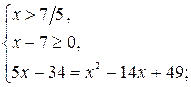
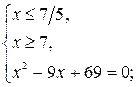
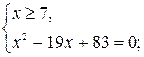
![]()
![]()
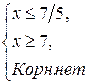

Ответ: 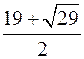 .
.
· Иррациональные показательные уравнения:
а) Решить уравнение
![]()
Решение.
![]() ОДЗ:
ОДЗ: ![]()
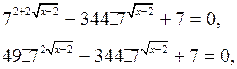
Пусть ![]() = t, t > 0
= t, t > 0
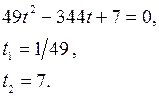
Сделаем обратную замену:
![]() = 1/49, или
= 1/49, или ![]() = 7,
= 7,
![]() =
= ![]() ,
, ![]()
![]() – (ур-ние не имеет решений) x = 3.
– (ур-ние не имеет решений) x = 3.
Ответ: 3
б) Решить уравнение
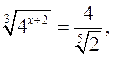
Решение.
Приведем все степени к одному основанию 2:
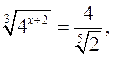
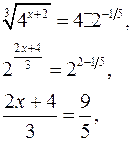 данное уравнение равносильно уравнению:
данное уравнение равносильно уравнению:
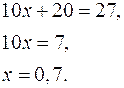
Ответ: 0,7
· Иррациональное уравнение, содержащее иррациональность четной степени:
Решить уравнение ![]()
Решение.
![]() возведем обе части уравнения в квадрат
возведем обе части уравнения в квадрат
3x – 5 – 2![]()
2x – 2 = 2![]()
x –1 = ![]()
x![]() Проверка:
Проверка:
x![]() x = 3,
x = 3, ![]()
4x![]() 1 = 1.
1 = 1.
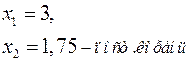 x = 1,75
x = 1,75 ![]()
Ответ: 3.
· Иррациональное уравнение, содержащее иррациональность нечетной степени:
Решить уравнение ![]()
Решение.
![]() возведем обе части уравнения в куб
возведем обе части уравнения в куб
![]()
![]() но
но ![]() , значит:
, значит:
![]()
![]() возведем обе части уравнения в куб
возведем обе части уравнения в куб
(25 + x)(3 – x) = 27,
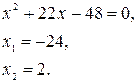
Ответ: –24; 2.
· Иррациональные уравнения, которые решаются заменой:
а) Решить уравнение 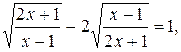
Решение.
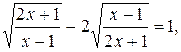
Пусть 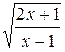 = t, тогда
= t, тогда 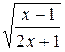 =
= ![]() , где t > 0
, где t > 0
t – ![]()

Сделаем обратную замену:
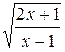 = 2, возведем обе части в квадрат
= 2, возведем обе части в квадрат
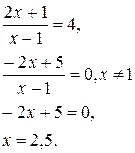 Проверка: x = 2,5
Проверка: x = 2,5 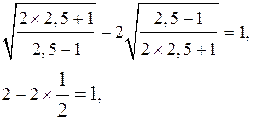
Ответ: 2,5.
б) Решить уравнение ![]()
Решение.
![]()
Пусть ![]() = t, значит
= t, значит ![]() =
= ![]() , где t > 0
, где t > 0
t![]() + t – 6 = 0,
+ t – 6 = 0,
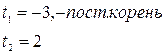
Сделаем обратную замену:
![]() = 2, возведем обе части уравнения в четвертую степень
= 2, возведем обе части уравнения в четвертую степень
x![]() + 8 = 16, Проверка:
+ 8 = 16, Проверка:
x![]() = 8, x = 2,
= 8, x = 2, ![]()
x = 2. 6 = 6
Ответ: 2.
в) Решить уравнение ![]()
Решение.
![]()
![]()
Пусть ![]() = t, где t > 0
= t, где t > 0
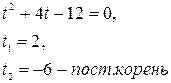
Сделаем обратную замену:
![]() = 2, возведем обе части уравнения в квадрат
= 2, возведем обе части уравнения в квадрат
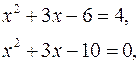 Проверка:
Проверка: ![]()
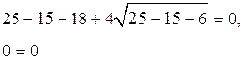
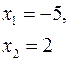
![]() ,
, 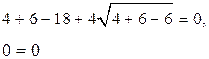
Ответ: –5; 2.
Решение сложных иррациональных уравнений:
· Иррациональное уравнение, содержащее двойную иррациональность:
Решить уравнение ![]()
Решение.
![]() возведем обе части уравнения в куб
возведем обе части уравнения в куб
![]()
![]() возведем обе части уравнения в квадрат
возведем обе части уравнения в квадрат
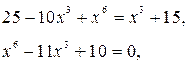
Пусть ![]() = t
= t
t 2– 11t + 10 = 0,
![]()
![]()
Сделаем обратную замену: Проверка:
![]() = 10, или
= 10, или ![]() = 1, x =
= 1, x = ![]() ,
, ![]()
x = ![]() -пост. корень
-пост. корень ![]() 0
0 ![]()
![]()
Ответ: 1.
x = 1, ![]()
1 = 1
· Иррациональные логарифмические уравнения:
а) Решить уравнение lg3 + 0,5lg(x – 28) = lg![]()
Решение.
lg3 + 0,5lg(x – 28) = lg![]() ,
,
lg(3![]() = lg
= lg![]() ,
,
Учитывая ОДЗ, данное уравнение равносильно системе:
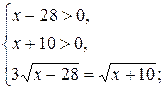
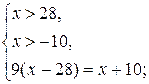
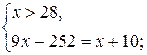
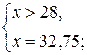
Ответ: 32,75
б) Решить уравнение ![]()
Решение.
![]()
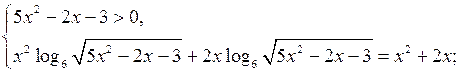
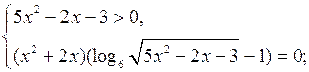
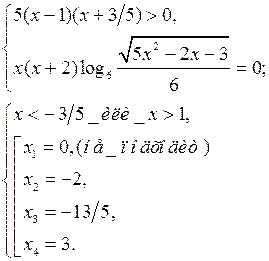
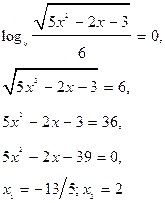
Ответ: ![]() ; – 2; 3.
; – 2; 3.
IV. Иррациональные неравенства
Неравенства называются иррациональными, если его неизвестное входит под знак корня (радикала).
Иррациональное неравенство
вида ![]() равносильно системе неравенств:
равносильно системе неравенств:
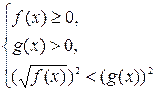
Иррациональное неравенство
вида ![]() равносильно совокуп-ности двух систем неравенств:
равносильно совокуп-ности двух систем неравенств:
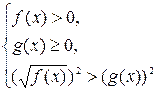 и
и 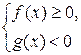
Решение иррациональных неравенств стандартного вида:
а) Решить неравенство ![]()
Решение.
![]()
Данное неравенство равносильно системе неравенств:
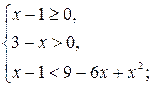
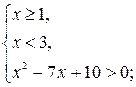
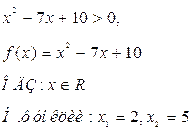
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
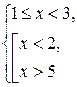 + – +
+ – +
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: [1; 2).![]() 1
3 x
1
3 x
б) Решить неравенство ![]()
Решение.
![]()
Данное неравенство равносильно двум системам неравенств:
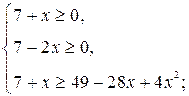
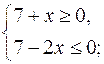
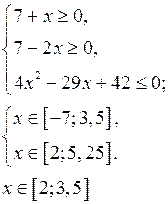
Ответ: ![]()
в) Решить неравенство ![]()
Решение.
![]()
Данное неравенство равносильно системе неравенств:
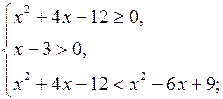
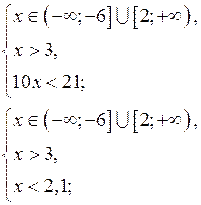
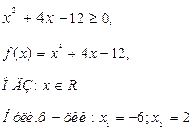
Ответ: нет решений![]()
Решение иррациональных неравенств нестандартного вида:
а) Решить неравенство ![]()
Решение.
![]()
Данное неравенство равносильно системе неравенств:
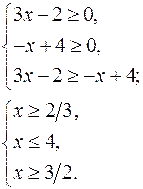
Ответ: ![]()
б) Решить неравенство![]()
Решение.
![]()
Данное неравенство равносильно системе неравенств:
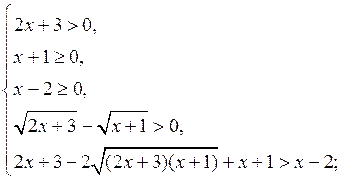
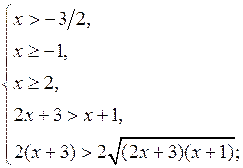
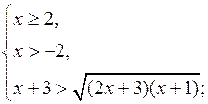
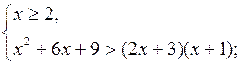
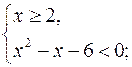
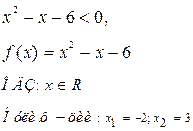
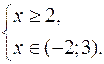
Ответ: ![]()
· Решение иррациональных неравенств с помощью правила знаков при умножении и делении:
а) Решить неравенство 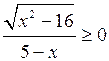
Решение.
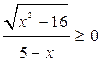
Учитывая то, что ![]()
![]() и правило знаков при делении данное неравенство равносильно системе
неравенств:
и правило знаков при делении данное неравенство равносильно системе
неравенств:
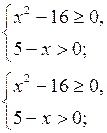
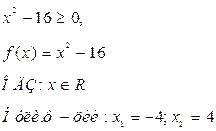
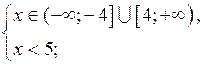
Ответ: ![]()
б) Решить неравенство (2x – 5)![]()
Решение.
(2x – 5)![]()
Учитывая то, что ![]() и правило знаков при делении данное неравенство равносильно системе
неравенств:
и правило знаков при делении данное неравенство равносильно системе
неравенств:
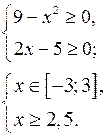
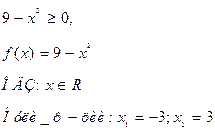
Ответ: ![]()
· Решение иррациональных неравенств способом группировки:
Решить неравенство ![]()
Решение.
![]() ,
,
![]() сгруппируем по два слагаемых
сгруппируем по два слагаемых
![]()
![]()
![]() вынесем общий множитель за скобку
вынесем общий множитель за скобку
![]() учитывая, что
учитывая, что ![]() > 0 и правило знаков при умножении данное неравенство равносильно системе неравенств:
> 0 и правило знаков при умножении данное неравенство равносильно системе неравенств:
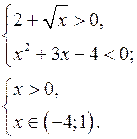
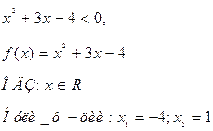
Ответ: ![]() ( 0; 1 )
( 0; 1 )
· Иррациональное неравенство, содержащее два знака иррациональности:
Решить неравенство ![]()
Решение.
![]()
Данное неравенство равносильно системе неравенств:
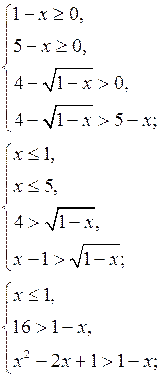
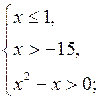
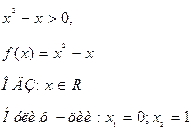
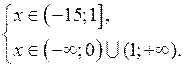
Ответ: ![]()
· Решение иррациональных неравенств заменой:
Решить неравенство 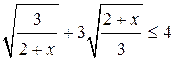
Решение.
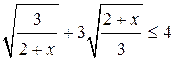
Пусть 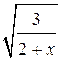 = t, тогда
= t, тогда 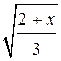 =
= ![]() , t
> 0
, t
> 0
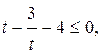
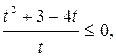
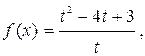
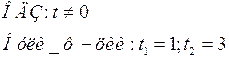
![]()
Сделаем обратную замену:
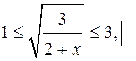 возведем в квадрат обе части неравенства
возведем в квадрат обе части неравенства
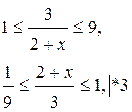
![]()
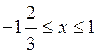
Ответ: 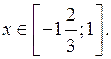
Решение иррациональных неравенств смешанного вида:
· Иррациональные показательные неравенства:
а) Решить неравенство ![]()
Решение.
![]() ,
,
![]() т.к. y = 0,8t
т.к. y = 0,8t![]() , то
, то
0,5x(x – 3) < 2,
0,5x2 – 1,5x – 2 < 0,
x2 – 3x – 4 < 0,
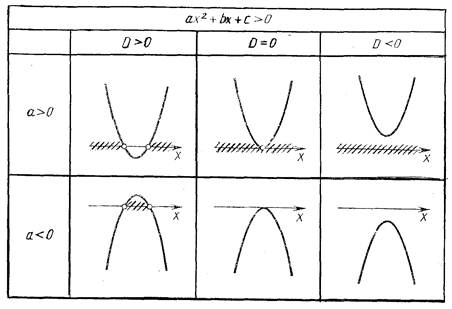
f(x) = x2 – 3x – 4,
ОДЗ![]() ,
+ – +
,
+ – +
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Нули функции: x1 = 4; x2 = – 1. –1 4 x
Нули функции: x1 = 4; x2 = – 1. –1 4 x
Ответ: х![]()
б) Решить неравенство 4![]() – 2
– 2![]() < 2
< 2![]() – 32
– 32
Решение.
4![]() – 2
– 2![]() < 2
< 2![]() – 32, ОДЗ:
x > 0
– 32, ОДЗ:
x > 0
2![]() – 2
– 2![]()
![]() 2 < 2
2 < 2![]()
![]() 24 – 25, выполним группировку слагаемых
24 – 25, выполним группировку слагаемых
2![]() (2
(2![]() – 2) – 24(2
– 2) – 24(2![]() –2) < 0,
–2) < 0,
(2![]() – 2)
– 2) ![]() (2
(2![]() – 24) < 0, учитывая правило знаков и ОДЗ данное неравенство равносильно 2-м системам:
– 24) < 0, учитывая правило знаков и ОДЗ данное неравенство равносильно 2-м системам:
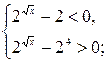 или
или 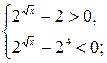
![]()
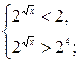 т.к. y = 2t
т.к. y = 2t![]() , то
, то 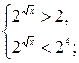 т.к. y = 2t
т.к. y = 2t![]() , то
, то
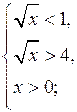
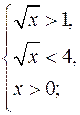
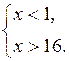
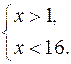
![]()
![]()
Ответ: х![]()
· Решение иррациональных логарифмических неравенств:
Решить
неравенство 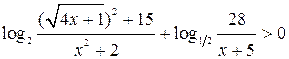
Решение.
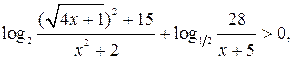 уч. ОДЗ данное нер-во равносильно системе нер-ств
уч. ОДЗ данное нер-во равносильно системе нер-ств
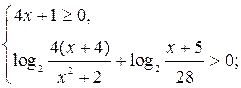
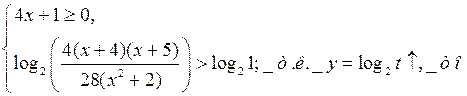
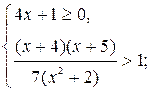
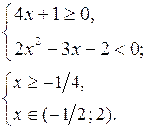
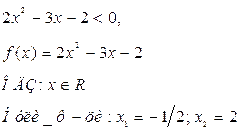
Ответ: ![]()
V. Вывод
Реферат помог мне научиться решать иррациональные уравнения и неравенства следующих типов: стандартные, показательные, содержащие знак модуля, логарифмические, повышенного уровня.
Примеры взяты и подробно разобраны не только из школьной программы, но и из вступительных экзаменов в школу А.Н. Колмогорова при МГУ, из сборника задач по математике под редакцией М.И. Сканави.
Этот материал может быть интересен и полезен выпуск – никам школ и абитуриентам технических вузов.

VI. Список литературы
1) Алгебра и начала анализа. Под редакцией А.Н. Колмогорова
2) 3000 конкурсных задач по математике. Авторы: Е.Д. Куланин, В.П. Норин
3) Справочные материалы по математике. Авторы: В.А. Гусев, А.Г. Мордкович
4) Сборник задач по математике. Под редакцией М.И. Сканави
5) Справочный материал
Похожие работы
... проведении исследования были решены следующие задачи: 1) Проанализированы действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств. Проведенный анализ позволяет сделать следующие выводы: ·в средней школе недостаточное внимание уделяется методам решения различных иррациональных уравнений, в основном ...
... решения обязательно выполняется проверка. Не обращается внимание на то, что иррациональные уравнения могут решаться и с использованием понятия равносильности. В данном параграфе представлены различные виды иррациональных уравнений, которые можно отнести к стандартным и решать одним из следующих методов, а именно: 1) метод перехода к уравнению - следствию с последующей проверкой полученных корней ...
... литературы дается характеристика этих форм, разработана методика применения самостоятельной работы вместе с иными формами организации познавательной деятельности на факультативных занятиях в выпускных классах средней школы, изучены учебные возможности учащихся в экспериментальной группе, проведена опытно- экспериментальная работа по включению самостоятельной работы школьников в процесс обучения. ...
... на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями. 2. Методика изучения неравенств в старших классах 2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики Ввиду важности и обширности материала, ...
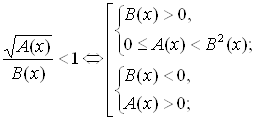
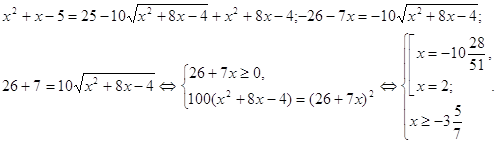
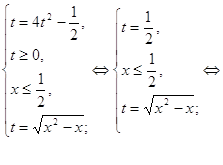
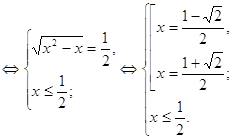

0 комментариев