Методика решения иррациональных уравнений и неравенств в школьном курсе математики

Содержание

Введение

§ 1. Анализ школьных учебников по алгебре и началам анализа

1.1. «Алгебра, 8», авт. А. Г. Мордкович

1.2. «Алгебра и начала анализа, 10-11», авт. А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницин и др..

1.3. «Алгебра и начала анализа, 10-11», авт. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др..

1.4. «Алгебра и начала анализа, 10-11», авт. М. И. Башмаков.

1.5. «Алгебра и начала анализа, 10-11», авт. А. Г. Мордкович.

1.6. «Сборник задач по алгебре, 8-9», авт. М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич.

1.7. «Алгебра и математический анализ, 11», авт. Н. Я. Виленкин, О.С. Ивашев-Мусатов, С. И. Шварцбурд.

§ 2. Методика изучения иррациональных уравнений

2.1. Теоретические основы решения уравнений

2.1.1. Основные понятия, относящиеся к уравнениям

2.1.2. Наиболее важные приемы преобразования уравнений

2.2. Методы решения иррациональных уравнений

2.2.1. Метод сведения к эквивалентной системе уравнений и неравенств

2.2.2. Метод уединения радикала

2.2.3. Метод введения новой переменной.

2.2.4. Метод сведения к эквивалентным системам рациональных уравнений

2.2.5. Умножение обеих частей уравнения на функцию.

2.2.6. Решение иррациональных уравнений с использованием свойств входящих в них функций

3. Тождественные преобразования при решении иррациональных уравнений

§ 3. Методика решения иррациональных неравенств

3.1. Теоретические основы решения иррациональных неравенств

3.2. Методы решения иррациональных неравенств

3.2.1. Метод сведения к эквивалентной системе или совокупности рациональных неравенств

3.2.2. Умножение обеих частей неравенства на функцию

3.2.3. Метод введения новой переменной

3.2.4. Решение иррациональных неравенств с использованием свойств входящих в них функций

§ 4. Опытное преподавание

Заключение

Список библиографии

Приложение А

Приложение Б

Приложение В

Введение

Материал, связанный с уравнениями и неравенствами, составляет значительную часть школьного курса математики. Одним из сложных разделов алгебры, изучаемых в школьной программе, являются иррациональные уравнения и неравенства, так как в школе им уделяют достаточно мало внимания.

Трудности при изучении данного вида уравнений и неравенств связаны со следующими их особенностями:

·  в большинстве случаев отсутствие четкого алгоритма решения иррациональных уравнений и неравенств;

·  при решении уравнений и неравенств данного вида приходится делать преобразования, приводящие к уравнениям (и неравенствам), не равносильным данному, вследствие чего чаще всего возникают ошибки, которые обычно связаны с потерей или приобретением посторонних корней в процессе решения.

Опыт показывает, что учащиеся в недостаточной степени овладевают умением решать иррациональные уравнения и неравенства, часто допускают ошибки при их решении. Однако задачи по теме «Иррациональные уравнения и неравенства» встречаются на вступительных экзаменах, и они довольно часто становятся «камнем преткновения».

Выше изложенное обусловило проблему исследования: обучение школьников решению иррациональных уравнений и неравенств, используя при этом основные методы решения иррациональных уравнений различных видов.

Объектом исследования является процесс обучения алгебре в 7-9 классах и алгебре и началам анализа в 10-11 классах.

Предметом исследования являются различные виды иррациональных уравнений и неравенств и методы их решения.

Целью работы является разработка методики изучения учащимися иррациональных уравнений и неравенств в школе.

Гипотеза исследования: освоение умения различать основные виды иррациональных уравнений и неравенств, умения применять необходимые приемы и методы их решения позволит учащимся решать иррациональные уравнения и неравенства на сознательной основе, выбирать наиболее рациональный способ решения, применять разные способы решения, в том числе те, которые не рассмотрены в школьных учебниках.

Для достижения поставленной цели и проверки гипотезы необходимо решить следующие задачи:

1.  проанализировать действующие учебники алгебры и начала математического анализа для выявления представленной в них методики решения иррациональных уравнений и неравенств;

2.  изучить стандарты образования по данной теме;

3.  изучить статьи и учебно-методическую литературу по данной теме;

4.  подобрать теоретический материал, связанный с равносильностью уравнений и неравенств, равносильностью преобразований, методами решения иррациональных уравнений и неравенств;

5.  рассмотреть основные методы и приемы решения различных иррациональных уравнений и неравенств;

6.  подобрать примеры решения иррациональных уравнений и неравенств для демонстрации излагаемой теории;

7.  разработать

8.  осуществить опытное преподавание.

§ 1. Анализ школьных учебников по алгебре и началам анализа

При изучении любой новой темы в основном курсе школы встает проблема изложения данной темы в школьных учебниках. Пропедевтикой изучения раздела иррациональных уравнений и неравенств в школе является введение понятие арифметического корня и, соответственно, рассмотрение его свойств.

Проанализируем в каких классах вводится данное понятие разными авторами учебников. Алимов Ш. А. в учебнике «Алгебра. 9класс» вводит понятие арифметического корня натуральной степени, а также свойства арифметического корня. Макарычев Н. Г. же разделяет понятия квадратного корня и корня -ой степени. В учебнике «Алгебра. 8 класс» классе вводится понятие арифметического квадратного корня и, соответственно, рассматриваются его свойства. В учебнике «Алгебра. 9 класс» вводятся понятия корня -ой степени, арифметического корня -ой степени и рассматриваются свойства арифметического корня -ой степени. Колмогоров А. Н. в учебнике «Алгебра. 10 класс» вводит понятия корня -ой степени, арифметического корня -ой степени и рассматривает свойства арифметического корня -ой степени перед изучением иррациональных уравнений. Мордкович А. Г. в учебнике «Алгебра. 8 класс» вводит понятие квадратного корня и его свойства. Кроме того, в этом же учебнике есть отдельный параграф, посвященный иррациональным уравнениям.

1.1. «Алгебра, 8», авт. А. Г. Мордкович [27], [28]

Данное учебное пособие состоит из двух частей: учебника и задачника.

В I части данного учебного пособия материал, посвященный иррациональным уравнениям, изложен в главе «Квадратные уравнения» в параграфе «Иррациональные уравнения». Параграф начинается с определения иррационального уравнения. Далее рассматривается решение иррационального уравнения  по определению квадратного корня из чего выводится метод решения иррациональных уравнений – метод возведения в квадрат обеих частей уравнения. Затем данный метод демонстрируется на примерах решения иррациональных уравнений вида , . Найденные корни проверяются подстановкой в исходное уравнение, при этом обращено внимание на те случаи, когда могут появиться посторонние корни. Автор подчеркивает, что проверка – обязательный этап решения иррационального уравнения. Далее приводится решение уравнения вида  методом введения новой переменной . Параграф завершается беседой о равносильных и неравносильных преобразованиях: дается определение равносильных уравнений, перечисляются и демонстрируются на примерах равносильные и неравносильные преобразования.

Система задач во II части данного учебного пособия достаточно разнообразна. В №№ 1011-1014 необходимо решить иррациональные уравнения вида , где  – линейное, квадратное или дробно-рациональное выражение. В № 1015 чтобы решить уравнение необходимо сначала уединить радикал. В № 1016 для решения предложены уравнения вида . №№ 10017-1020 –упражнения для решения методом замены иррациональных уравнений вида , , . В №№ 1023, 1024 необходимо выяснить, равносильны ли уравнения. В №№ 1021, 1022, 1025-1027 нужно решить уравнения вида , , где выражения , могут быть как линейными так и квадратными, а в №№ 1028-1031 – уравнения вида .

№№ 1032, 1033 – упражнения повышенной трудности для решения иррациональных уравнений методом замены.

Теперь проанализируем действующие учебники по алгебре и началам математического анализа для 10-11 классов, чтобы выяснить, как в них представлены методы решения иррациональных уравнений и неравенств.

1.2. «Алгебра и начала анализа, 10-11», авт. А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницин и др. [13].

Материал по данной теме изложен в IV главе «Показательная и логарифмическая функции», как пункт «Иррациональные уравнения» параграфа «Обобщение понятия степени». Автор рекомендует рассматривать решение иррациональных уравнений в теме «Уравнения, неравенства, системы», где систематизируются сведения об уравнениях.

В пункте «Иррациональные уравнения» дается понятие иррационального уравнения, приводится несколько примеров простейших иррациональных уравнений вида  , которые решаются с помощью возведения обеих частей уравнения в квадрат. Найденные корни проверяются подстановкой в исходное уравнение, при этом обращено внимание на те случаи, когда могут появиться посторонние корни. Показано, что кроме возведения в квадрат иррациональные уравнения удобно решать, используя равносильный переход от уравнения к системе, состоящей из уравнения и неравенства. Рассмотрен пример иррационального уравнения, содержащего корень третьей степени. Для того чтобы «избавиться от радикала», обе части такого уравнения возводятся в куб.

После пункта приведены упражнения для закрепления умений решать иррациональные уравнения. В №№417-420 предложены простейшие уравнения вида  , решить которые можно с помощью возведения обеих частей уравнения либо в квадрат, либо в куб, а также используя равносильные переходы. Такие задачи, по мнению авторов учебника необходимо уметь решать для получения удовлетворительной оценки. Задачи же в №№422-425 чуть сложнее. Здесь уравнения содержат корни выше третьей степени.

Иррациональным неравенствам в данном пункте внимания не уделено.

В заключительной главе учебника «Задачи на повторение» помещены практические упражнения для повторения курса. Здесь в параграфе «Уравнения, неравенства, системы уравнений и неравенств» иррациональным уравнениям и неравенствам посвящен пункт «Иррациональные уравнения и неравенства». То есть, не смотря на то, что в основной части учебника иррациональным неравенствам внимания не уделено, автор включает в задания для повторения такие неравенства.

1.3. «Алгебра и начала анализа, 10-11», авт. Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. [1].

В данном учебнике нет материала, посвященного иррациональным уравнениям и неравенствам. Лишь в конце ученика помещены упражнения для итогового повторения курса алгебры. Здесь есть только один номер для решения простейших иррациональных уравнений (№801). Упражнений для решения иррациональных неравенств нет.

Это можно объяснить тем, что, по мнению автора, умение решать иррациональные неравенства не является обязательным для учащихся и соответствующая тема может быть предложена для изучения самостоятельно или на факультативных занятиях. [14] Поэтому в учебнике предложены задачи для внеклассной работы, где встречаются иррациональные уравнения (№№934, 947) и неравенства (№942).

1.4. «Алгебра и начала анализа, 10-11», авт. М. И. Башмаков [2].

В данном учебном пособии иррациональные уравнения и неравенства рассматриваются в заключительной VI главе «Уравнения и неравенства». Глава предназначена для систематизации и обобщения сведений об уравнениях, неравенствах и системах уравнений. В начале главы помещена вводная беседа, которая состоит из трех пунктов.

В пункте «Уравнение» вводятся такие понятия как уравнение, неизвестные, корень уравнения, подробно рассказывается, что значит решить уравнение с одним или двумя неизвестными, что означает найти корни уравнения, приведены некоторые рекомендации о форме записи ответа при решении уравнений с одним или двумя неизвестными.

В пункте «Равносильность» выясняется, когда одно уравнение является следствием другого, вводится понятие равносильных уравнений. Автор подробно останавливается на некоторых полезных преобразованиях уравнений:

1)  Перенос членов из одной части уравнения в другую с противоположным знаком.

2)  Переход к совокупности уравнений.

3)  Переход к системе уравнений.

Все равносильные переходы представлены в виде схем и рассмотрены на примерах.

В следующем пункте «Неравенство» приведены примеры верных и неверных числовых неравенств, основные правила преобразования неравенств, при этом используются знаки следствия и равносильности. Вводятся такие понятия как ОДЗ неравенства, решение неравенства, равносильные неравенства, выясняется, когда одно неравенство является следствием другого.

§1 «Уравнения с одним неизвестным» состоит из трех пунктов: «Общие приемы», «Примеры решения уравнений» и «Приближенные методы вычисления корней». В первом пункте перечислены стандартные уравнения, которые были изучены ранее. Основным шагом в решении уравнения является преобразование уравнения к одному из стандартных. Приведены некоторые наиболее употребительные приемы, общие для всех типов уравнений:

1)  Разложение на множители.

2)  Введение нового неизвестного.

3)  Графический метод.

Отметим, что во втором пункте на ряду со стандартными уравнениями рассматривается решения только одного простейшего иррационального уравнения с помощью равносильного перехода к системе.

В третьем пункте кратко рассказывается о таких методах приближенного вычисления корней как метод половинного деления, метод хорд и касательных.

§ 2 «Неравенства с одним неизвестным» состоит из двух пунктов: «Общие приемы» и «Примеры решения неравенств». В первом пункте демонстрируется два приема решения неравенств: разложение на множители и метод замены неизвестного.

Во втором пункте на примерах показана техника решения неравенств с помощью переходов, сохраняющих равносильность. Отметим, что на ряду со стандартными неравенствами рассматривается решение только одного простейшего иррационального неравенства.

В конце главы помещены задания для решения иррациональных уравнений №17, для решения иррациональных неравенств – №21, в котором есть задание со звездочкой, то есть относящееся к разделу «трудные задачи».

Иррациональным уравнениям и неравенствам в главе уделено недостаточно внимания: приведены решения с помощью переходов, сохраняющих равносильность одного простейшего иррационального уравнения и одного неравенства.

Цель данной главы – обобщить имеющиеся у учащихся знаний об уравнениях, неравенствах и системах уравнений, поэтому здесь подробно не рассматриваются конкретные виды уравнений, а лишь повторяются сведения об изученных видах уравнений и методах их решения. [14]

1.5. «Алгебра и начала анализа, 10-11», авт. А. Г. Мордкович [10], [11].

Данное учебное пособие состоит из двух частей: учебника и задачника.

В I части данного учебного пособия материал, касающийся иррациональных уравнений и неравенств, изучается в последней VIII главе «Уравнения и неравенства. Системы уравнений и неравенств», завершающей изучение школьного курса алгебры и начал математического анализа. Здесь уравнения и неравенства рассматриваются с самых общих позиций. Это, с одной стороны, своеобразное подведение итогов и, с другой стороны, некоторое расширение и углубление знаний.

В первых трех параграфах этой главы подведены итоги изучения в школе уравнений, неравенств. Использованы следующие термины:

¨  равносильность уравнений, равносильность неравенств;

¨  следствие уравнения, следствие неравенства;

¨  равносильное преобразование уравнения, неравенства;

¨  посторонние корни (для уравнений);

¨  проверка корней (для уравнений).

Сформулированы теоремы:

¨  о равносильности уравнений;

¨  о равносильности неравенств.

Даны ответы на четыре главных вопроса, связанных с решением уравнений:

1)  как узнать, является ли переход от одного уравнения к другому равносильным преобразованием;

2)  какие преобразования переводят данное уравнение в уравнение-следствие;

3)  как сделать проверку, если она сопряжена со значительными трудностями в вычислениях;

4)  в каких случаях при переходе от одного уравнения к другому может произойти потеря корней и как этого не допустить?

Перечислены возможные причины расширения области определения уравнения, одна из которых – освобождение в процессе решения уравнения от знаков корней четной степени; указаны причины, по которым может произойти потеря корней при решении уравнений.

Выделены четыре общих метода решения уравнений:

1)  замена уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x);

2)  метод разложения на множители;

3)  метод введения новых переменных;

4)  функционально-графический метод.

Что касается иррациональных уравнений, то им в данном учебном пособии уделено достаточно большое внимание.

На примере иррационального уравнения показано как решение любого уравнения осуществляется в три этапа: технический, анализ решения, проверка.

Также на примере иррационального уравнения показано, как сделать проверку, если проверка корней с помощью их подстановки в исходное уравнение сопряжена со значительными вычислительными трудностями.

Метод замены уравнения h(f(x))=h(g(x)) уравнением f(x)=g(x) применятся при решении иррациональных уравнений для перехода от уравнения  к уравнению .

Метод введения новой переменной также разобран и на примере решения иррационального уравнения.

Отдельный пункт посвящен иррациональным неравенствам. Здесь с теоретическим обоснованием рассматривается решение неравенств вида , . В первом случае иррациональное неравенство заменяется равносильной системой неравенств 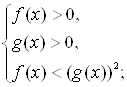 во втором – равносильной совокупностью систем неравенств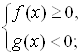

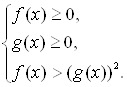
Система задач во II части данного учебного пособия изложена в той же последовательности, что и соответствующий материал в I части. В § 55 «Равносильность уравнений» изложены различные типы заданий на равносильность и следствие уравнений, в том числе и иррациональных. В § 56 «Общие методы решения уравнений» помещены задания для использования четырех методов, изложенных в I части данного учебного пособия, для решения уравнений. Все задачи в соответствии с ними разбиты на четыре блока, в каждом из которых встречаются иррациональные уравнения. В § 57 «Решение неравенств с одной переменной» изложены различные типы заданий на равносильность и следствие неравенств, в том числе и иррациональных.

В № 1673 нужно решить простейшие иррациональные уравнения. №№1674, 1675, 1712-1719 – упражнения выше среднего уровня для решения иррациональных уравнений, №№1790, 1791 – неравенств. № 1792 – упражнение повышенной трудности для решения иррациональных неравенств.

Много заданий, в которых требуется решить «смешанное» уравнение или неравенство, то есть логарифмическое, показательное или тригонометрическое уравнение или неравенство, в которое входят и иррациональные выражения. Среди этих заданий есть задания как базового, так и повышенного уровня.

В I части учебника много внимание уделено равносильности уравнений и неравенств, достаточно строго рассмотрены общие методы решения уравнений, с оговоркой о потере корней и приобретении посторонних. II часть учебника отличается обилием и разнообразием задач. Достаточно много задач на равносильность и следствие уравнений и неравенств.

1.6. «Сборник задач по алгебре, 8-9», авт. М. Л. Галицкий, А. М. Гольдман, Л. И. Звавич [5].

Данная книга представляет собой сборник задач по курсу алгебры, предназначенный для учащихся 8-9 классов с углубленным изучением математики.

В начале параграфа «Степень с рациональным показателем» помещен справочный материал теоретического характера, посвященный иррациональным уравнениям и неравенствам. Описаны такие пути решения иррациональных уравнений, как:

·  возведение обеих частей уравнения в натуральную степень с последующей проверкой найденных корней;

·  переход к равносильным системам, в которых учитывается область определения уравнения и требование того, что бы были неотрицательными обе части уравнения, возводимые в четную степень.

При решении иррациональных неравенств либо используется метод интервалов, либо с помощью равносильных преобразований заменяется данное иррациональное неравенство системой (или совокупностью систем) рациональных неравенств.

В параграфе рассмотрено три способа решения иррационального уравнения вида :

1)  переход к равносильной системе;

2)  введение новой переменной;

3)  использование свойства монотонности функций.

Среди упражнений, помещенных в данном параграфе, есть упражнения для закрепления умений и навыков решать иррациональные уравнения и неравенства. В №№115-117 необходимо доказать, что уравнение не имеет решения, в №№118-119 – ответить на вопрос: равносильны ли уравнения. №№120-144 предлагаются для решения иррациональных уравнений, №№145-155 – для решения неравенств описанными выше способами.

1.7. «Алгебра и математический анализ, 11», авт. Н. Я. Виленкин, О.С. Ивашев-Мусатов, С. И. Шварцбурд [4].

Данное учебное пособие представляет собой продолжение книги «Алгебра и начала анализа» для 10 класса и предназначено как для общеобразовательной школы, так и классов и школ с углубленным изучением курса математики.

Иррациональные уравнения и неравенства изучаются в параграфе «Степенная функция. Иррациональные выражения, уравнения и неравенства» VIII главы «Показательная, логарифмическая и степенные функции».

Пункт «Иррациональные уравнения» начинается с определения иррационального уравнения и примеров таких уравнений. Далее сформулирована и доказана теорема о равносильных уравнениях, на которой основано решение иррациональных уравнений. Из теоремы следует, что если в ходе решения иррационального уравнения приходилось возводить обе его части в степень с четным показателем, то могут появиться посторонние корни. Поэтому, чтобы не было необходимости подставлять найденные корни в данное уравнение, сформулировано еще два утверждения о равносильном переходе от уравнений вида  и  к системам, состоящим из уравнения и неравенства. Далее на примерах решения иррациональных уравнений демонстрируются данные равносильные переходы. Также автор рекомендует перед возведением обеих частей уравнения в некоторую степень «уединить радикал», то есть представить уравнение в виде . Далее данный метод применяется для решения иррациональных уравнений

После данного пункта помещены упражнения для закрепления умений решать иррациональные уравнения описанными выше методами – №216. В №215 необходимо доказать, что данные иррациональные уравнения не имеют решений.

В следующем пункте «Иррациональные неравенства» сформулированы приемы решения иррациональных неравенств вида  и  с помощью равносильного перехода к системе неравенств в первом случае и совокупности систем неравенств – во втором. Рассматривается решение иррационального неравенства вида  с помощью равносильного перехода к неравенству . Решение каждого из видов неравенств демонстрируется на примерах.

После данного пункта помещены упражнения (№217) для закрепления умения решать иррациональные неравенства с помощью равносильных переходов, описанных выше.

Все утверждения, сформулированные в данном учебном пособии, изложены со строгим обоснованием. Описан полезный метод при решении иррациональных уравнений – метод «уединения радикала». Не смотря на то, что учебник не отличается обилием упражнений, предлагаемые задания разнообразны, различной степени сложности

Проведенный анализ позволяет сделать следующие выводы:

1)  В учебнике [1] материала по методам решения иррациональных уравнений нет. В учебниках [13] и [4] материала по теории способов решения иррациональных уравнений достаточно. В большом объеме теория по общим методам решения рассмотрена учебнике [2] и [10].

2)  В каждом учебнике рассмотрены два основных способа решения: возведение обеих частей уравнения в степень, с последующей подстановкой полученных корней в исходное уравнение, а также решение уравнений с помощью равносильных переходов к системе, состоящей из уравнения и неравенства. В учебниках [2] и [10] рассмотрены такие общие методы решения уравнений как метод разложения на множители, метод введения новых переменных, функционально-графический метод; некоторые из них продемонстрированы на примерах решения иррационального уравнения.

3)  В учебниках [1] и [13] не рассмотрено решение иррациональных неравенств. В учебнике [2] материала по решению иррациональных неравенств не достаточно. В учебниках [4] и [10] подробно и с теоретическим обоснованием рассмотрено решение иррациональных неравенств вида ,  с помощью равносильного перехода к системе (или совокупности систем). Только в учебнике [4] рассматривается решение иррационального неравенства вида .

4)  Наиболее большой объем упражнений для решения иррациональных уравнений и неравенств представлен в учебниках [11] и [5]. В учебнике [4] упражнений немного, но они разнообразны.

§ 2. Методика изучения иррациональных уравнений

Похожие работы

Методика изучения неравенств

Скачать

37778

0

2

... на основе знания связи между результатом и компонентами арифметических действий (т.е. знания способов нахождения неизвестных компонентов). Эти требования программы определяют методику работы над уравнениями. 2. Методика изучения неравенств в старших классах 2.1 Содержание и роль линии уравнений и неравенств в современном школьном курсе математики Ввиду важности и обширности материала, ...

Самостоятельная работа как средство обучения решению уравнений в 5-9 классах

Скачать

123013

25

0

... на качественно новую ступень овладения содержанием школьной математики. Глава II. Методико - педагогические основы использования самостоятельной работы, как средство обучения решению уравнений в 5 - 9 классах.   § 1. Организация самостоятельной работы при обучения решению уравнений в 5 - 9 классах.   При традиционном способе преподавания учитель часто ставит ученика в положение объекта ...

Формирование умения решения квадратных уравнений в 8 классе

Скачать

46858

6

0

... , можно сделать вывод о недостаточном освещении изучаемого вопроса в современной методической литературе. Объект исследования работы: процесс обучения математике. Предмет: формирование умения решения квадратных уравнений у учащихся 8-го класса. Контингент: учащиеся 8-го класса. Глава 1. Теоретические аспекты обучению решения уравнений в 8 классе   1.1.  Из истории возникновения квадратных ...

Методика изучения функций в школьном курсе математики

Скачать

20346

1

2

... числового аргумента, поэтому при таком подходе наблюдается определённая избыточность в формировании функции как обобщённого понятия. 2. Основные направления введения понятия функции в школьном курсе математики В современном школьном курсе математики ведущим подходом считается генетический с добавлением элементов логического. Формирование понятий и представлений, методов и приёмов в составе ...