Навигация
Уравнение электрических колебаний в проводах
1.1.2. Уравнение электрических колебаний в проводах.
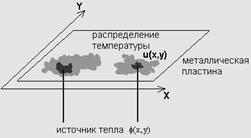
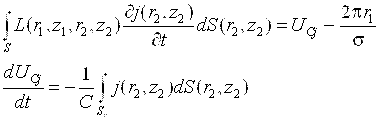
Как указывалось выше, к уравнению (1) приводит и задача об электрических колебаниях в проводах. Электрический ток в проводе характеризуется величиной i (x, t) и напряжением v (x, t), которые зависят от координаты x точки провода и от времени t. Рассматривая элемент провода ![]() , можем написать, что падение напряжения на элементе
, можем написать, что падение напряжения на элементе ![]() равно
равно ![]() . Это падение напряжения складывается из омического, равного
. Это падение напряжения складывается из омического, равного ![]() , и индуктивного, равного
, и индуктивного, равного ![]() . Итак,
. Итак,
![]() (4)
(4)
где R и L – сопротивление и коэффициент индуктивности, рассчитанные на единицу длины провода. Знак минус взят потому, что ток течет в направлении, обратном возрастанию v. Сокращая на ![]() , получаем уравнение
, получаем уравнение
![]() (5)
(5)
Далее, разность токов, выходящего из элемента ![]() и входящего в него за время
и входящего в него за время ![]() , будет
, будет
![]()
Она расходуется на зарядку элемента, равную ![]() , и на утечку через боковую поверхность провода вследствие несовершенства изоляции, равную
, и на утечку через боковую поверхность провода вследствие несовершенства изоляции, равную ![]() (здесь А – коэффициент утечки). Приравнивая эти выражения и сокращая на
(здесь А – коэффициент утечки). Приравнивая эти выражения и сокращая на ![]() , получим уравнение
, получим уравнение
![]() (6)
(6)
Уравнения (5) и (6)принято называть телеграфными уравнениями.
Из системы уравнений (5) и (6) можно получить уравнение, содержащее только искомую функцию i (x, t), и уравнение, содержащее только искомую функцию v (x, t). Продифференцируем члены уравнения (6) по x; члены уравнения (5) продифференцируем по t и умножим их на С. Произведя вычитание, получим:
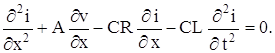
Подставляя в последнее уравнение выражение ![]() из уравнения (5), получим:
из уравнения (5), получим:
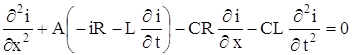
или
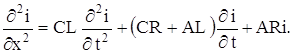 (7)
(7)
Аналогичным образом получается уравнение для определения v (x, t):
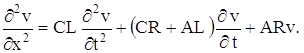 (8)
(8)
Если пренебречь утечкой через изоляцию ![]() и сопротивлением
и сопротивлением ![]() , то уравнения (7) и (8) переходят в волновые уравнения:
, то уравнения (7) и (8) переходят в волновые уравнения:
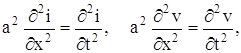
где обозначено: ![]() . Исходя из физических условий, формулируют граничные и начальные условия задачи.
. Исходя из физических условий, формулируют граничные и начальные условия задачи.
§1.2. Метод разделения переменных.
1.2.1. Уравнение свободных колебаний струны.
Метод разделения переменных или метод Фурье, является одним из наиболее распространенных методов решения уравнений с частными производными. Изложение этого метода мы проведем для задачи о колебаниях струны, закрепленной на концах. Итак, будем искать решение уравнения
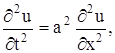
удовлетворяющее однородным граничным условиям
![]() (9)
(9)
и начальным условиям
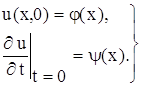 (10)
(10)
Уравнение (1) линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Имея достаточно большое число частных решений, можно попытаться при помощи суммирования их с некоторыми коэффициентами найти искомое решение.
Поставим основную вспомогательную задачу: найти решение уравнения
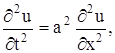
не равное тождественно нулю, удовлетворяющее однородным граничным условиям
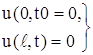 (11)
(11)
и представимое в виде произведения
![]() (12)
(12)
где X (x) – функция только переменного x, T (t) – функция только переменного t.
Подставляя предполагаемую форму решения (12) в уравнение (1), получим:
![]()
или, после деления на XT,
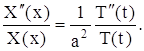 (13)
(13)
Чтобы функция (12) была решением уравнения (1), равенство (13) должно удовлетворяться тождественно, т. е. 0 ‹ х ‹ ![]() , t › 0. Правая часть равенства (13) является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства (13) при изменении своих аргументов сохраняют постоянное значение
, t › 0. Правая часть равенства (13) является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства (13) при изменении своих аргументов сохраняют постоянное значение
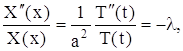 (14)
(14)
где ![]() – постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.
– постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке.
Из соотношения (14) получаем обыкновенные дифференциальные уравнения для определения функций X (x) и T (t)
![]() (15)
(15)
![]() (16)
(16)
Граничные условия (11) дают:
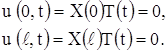
Отсюда следует, что функция X (x) должна удовлетворять дополнительным условиям:
X(0) = X(![]() ) = 0, (17)
) = 0, (17)
![]()
в то время как задача состоит в нахождении нетривиального решения. Для функции T (t) в основной вспомогательной задаче никаких дополнительных условий нет.
Таким образом, в связи с нахождением функции X (x) мы приходим к простейшей задаче о собственных значениях:
найти те значения параметра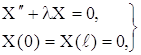 (18)
(18)
а также найти эти решения. Такие значения параметра ![]() называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи (18). Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.
называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи (18). Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.
Рассмотрим отдельно случаи, когда параметр ![]() отрицателен, равен нулю или положителен.
отрицателен, равен нулю или положителен.
1. При ![]() ‹ 0 задача не имеет нетривиальных решений. Действительно, общее решение уравнения (15) имеет вид
‹ 0 задача не имеет нетривиальных решений. Действительно, общее решение уравнения (15) имеет вид
![]()
Граничные условия дают:
Х (0) = С1 + С2 = 0;
![]()
![]()
т. е.
![]()
Но в рассматриваемом случае ![]() – действительно и положительно, так что
– действительно и положительно, так что ![]() . Поэтому
. Поэтому
С1 =0, С2 = 0
и, следовательно,
Х (х)![]() 0.
0.
2. При ![]() = 0 также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (15) имеет вид
= 0 также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения (15) имеет вид
Х (х) = С1х + С2.
Граничные условия дают:
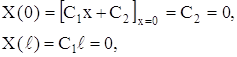
т. е. С1 = 0 и С2 = 0 и, следовательно,
Х (х)![]() 0.
0.
3. При ![]() › 0 общее решение уравнения может быть записано в виде
› 0 общее решение уравнения может быть записано в виде
![]()
Граничные условия дают:
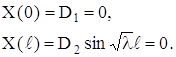
Если Х(х) не равно тождественно нулю, то D2![]() 0, поэтому
0, поэтому
![]() (19)
(19)
или
![]()
где n- любое целое число. Следовательно, нетривиальные решения задачи (18) возможны лишь при значениях
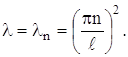
Этим собственным значениям соответствуют собственные функции
![]()
где Dn – произвольная постоянная.
Итак, только при значениях ![]() , равных
, равных
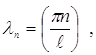 (20)
(20)
существуют нетривиальные решения задачи (11)
![]() (21)
(21)
определяемые с точностью до произвольного множителя, который мы положили равным единице. Этим же значениям ![]() n соответствуют решения уравнения (9)
n соответствуют решения уравнения (9)
![]() (22)
(22)
где An и Bn – произвольные постоянные.
Возвращаясь к задаче (1), (9), (10), заключаем, что функции
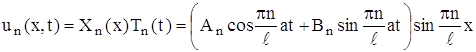 (23)
(23)
являются частными решениями уравнения (1), удовлетворяющими граничным условиям (11) и представимыми в виде произведения (12) двух функций, одна из которых зависит только от х, другая – от t. Эти решения могут удовлетворить начальным условиям (10) нашей исходной задачи только для частных случаев начальных функций j(x) и y(x).
Обратимся к решению задачи (1), (9), (10) в общем случае. В силу линейности и однородности уравнения (1) сумма частных решений
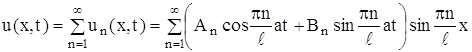 (24)
(24)
также удовлетворяет этому уравнению и граничным условиям (9). Начальные условия позволяют определить An и Bn. Потребуем, чтобы функция (24) удовлетворяла условиям (10)
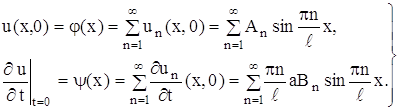 (25)
(25)
Из теории рядов Фурье известно, что произвольная кусочно-непрерывная и кусочно-дифференцируемая функция f(x), заданная в промежутке ![]() , разлагается в ряд Фурье
, разлагается в ряд Фурье
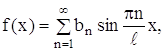 (26)
(26)
где
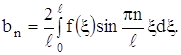 (27)
(27)
Если функции j(x) и y(x) удовлетворяют условиям разложения в ряд Фурье, то
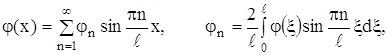 (28)
(28)
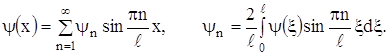 (29)
(29)
Сравнение этих рядов с формулами (25) показывает, что для выполнения начальных условий надо положить
![]() (30)
(30)
чем полностью определяется функция (24), дающая решение исследуемой задачи.
Итак, мы доказали, что ряд (24), где коэффициенты An и Bn определены по формуле (30), если он допускает двукратное почленное дифференцирование, представляет функцию u (x, t), которая является решением уравнения (1) и удовлетворяет граничным и начальным условиям (9) и (10).
Замечание. Решая рассмотренную задачу для волнового уравнения другим методом, можно доказать, что ряд (24) представляет решение и в том случае, когда он не допускает почленного дифференцирования. При этом функция ![]() должна быть дважды дифференцируемой, а
должна быть дважды дифференцируемой, а ![]() - один раз дифференцируемой.
- один раз дифференцируемой.
§2.1. Задачи, приводящие к уравнениям гиперболического типа.
Похожие работы
... менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения. 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики Уравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные ...
... цепи W1(s) = Wp(s) представлено как параллельное соединение простейших звеньев. 2.9 Неопределенность моделей систем управления Математические модели не отражают исчерпывающим образом динамические свойства систем управления в силу идеализации и упрощений, неизбежных при моделировании, неточной реализации алгоритмов управления и изменений характеристик объектов и других элементов в ...
... влияния – RТ и чистой воды – Rwдля некоторого момента времени 3.6. Выводы В нулевом и первом приближениях решена задача о температурном поле, вызванном закачкой радиоактивного раствора в глубокозалегающие пласты. На основании полученного решения установлены расчетные формулы для полей температуры, вызванных энергией распада и различием температур пласта и закачиваемой жидкости. ...
... влияния неодновременного включения блоков конденсаторных батарей. При этом рассматривался процесс обжима трубчатых заготовок из алюминиевого сплава АМг2М диаметром 27 мм, 57 мм, 87 мм и толщиной 1,2 мм одновитковым, четырехвитковым цилиндрическим, индуктором-концентратором. Рассматривалось пять типов магнитно-импульсных установок основные характеристики, которых приведены в табл.5.1. Таблица ...



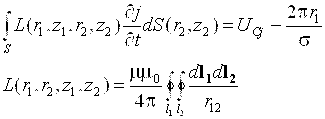
0 комментариев