Навигация
Операторы с определителем 1 сохраняют ориентацию пространства, а с определителем (-1) меняют ее на противоположную
Все собственные значения A - комплексные числа по модулю равные 1.
Кроме того, известны простейшие формы ортогональных матриц в ортонормированном правом базисе. Эти простейшие формы указаны в следующей таблице:
| dimV | det(A) = 1 | Название | det(A) = -1 | Название |
| 1 | I = (1) | Тождест-венный оператор | s = (-1) | Отраже-ние |
| 2 |
| Поворот на угол j |
| Отраже-ние |
| 3 |
| Поворот на угол j вокруг OZ |
| Зеркаль-ный пово-рот |
Замечание 1.
Учитывая связь между перемещением f и оператором f*, можно утверждать, что в подходящей декартовой системе координат имеет место формула:
R
= АR + v
, где А - одна
из матриц из
таблицы, а v
- некоторый
вектор.
Следовательно,
всякое перемещение
f имеет
обратное ![]() ,
которое задается
формулой R
=
,
которое задается
формулой R
= ![]() (R
- v
) =
(R
- v
) = ![]() R
-
R
- ![]() v.
Поскольку
матрица
v.
Поскольку
матрица ![]() - ортогональна,
обратное отображение
также является
перемещением.
Отметим еще,
что для всякой
ортогональной
матрицы P
и любого
вектора w преобразование
R
= PR +
w
является
перемещением.
- ортогональна,
обратное отображение
также является
перемещением.
Отметим еще,
что для всякой
ортогональной
матрицы P
и любого
вектора w преобразование
R
= PR +
w
является
перемещением.
Замечание 2.
Имеется существенное различие между математическим понятием перемещения и физическим понятием движения. Во втором случае имеется в виду непрерывное во времени изменение положения точки, в то время как в первом фиксируются только ее начальное и конечное положения.
Перемещения с det(A) = 1 можно представлять себе и как движения, в то время как при det(A)= -1 такое представление невозможно, если оставаться в пределах исходного пространства X.
Классификация перемещений.
Напомним, что
нам уже известны
некоторые
перемещения.
Перемещениями
прямой ![]() являются
тождественное
преобразование
I,
перенос
являются
тождественное
преобразование
I,
перенос ![]() на вектор v
и отражение
на вектор v
и отражение
![]() относительно
точки О .
относительно
точки О .
Для
случая плоскости
![]() перемещениями
будут уже упомянутые
I
и
перемещениями
будут уже упомянутые
I
и ![]() ,
а также поворот
,
а также поворот
![]() вокруг точки
О на угол j
и отражение
вокруг точки
О на угол j
и отражение
![]() относительно
прямой l
. Определим
дополнительно
скользящее
отражение
относительно
прямой l
. Определим
дополнительно
скользящее
отражение ![]() как
комбинацию
отражения
относительно
прямой l
с переносом
на вектор vЅЅl
.
как
комбинацию
отражения
относительно
прямой l
с переносом
на вектор vЅЅl
.
Наконец,
для пространства
![]() мы
имеем перемещения
I
и
мы
имеем перемещения
I
и ![]() ,
а, кроме того
поворот
,
а, кроме того
поворот ![]() вокруг
оси, заданной
точкой О и единичным
направляющим
вектором w
на угол j
и отражение
вокруг
оси, заданной
точкой О и единичным
направляющим
вектором w
на угол j
и отражение
![]() относительно
плоскости p.
Определим
дополнительно
зеркальный
поворот
относительно
плоскости p.
Определим
дополнительно
зеркальный
поворот ![]() как комбинацию
отражения
относительно
плоскости,
заданной точкой
О и вектором
нормали n с поворотом
как комбинацию
отражения
относительно
плоскости,
заданной точкой
О и вектором
нормали n с поворотом
![]() и скользящее
отражение
и скользящее
отражение
![]() - композицию
отражения .
- композицию
отражения . ![]() относительно
плоскости p
и переноса на
вектор vЅЅp.
Наконец, определим
винтовое
перемещение
относительно
плоскости p
и переноса на
вектор vЅЅp.
Наконец, определим
винтовое
перемещение ![]() как комбинацию
поворота
как комбинацию
поворота ![]() и параллельного
переноса на
вектор hw.
и параллельного
переноса на
вектор hw.
Отметим,
что некоторые
из указанных
выше перемещений
являются частными
случаями других.
Например,
тождественное
перемещение
можно рассматривать
как перенос
на нулевой
вектор (или как
поворот на
нулевой угол),
отражение ![]() является частным
случаем скользящего
отражения
является частным
случаем скользящего
отражения ![]() при v
= 0
и т. д.
при v
= 0
и т. д.
Теорема 3 .
Каждое
перемещение
f в
![]() (n
= 1, 2, 3 ) суть одно
из следующих
:
(n
= 1, 2, 3 ) суть одно
из следующих
:
n = 1 ![]() ,
, ![]()
n = 2 ![]() ,
, ![]() ,
, ![]()
n = 3 ![]() ,
, ![]() ,
, ![]() .
.
Доказательство.
Как
уже отмечалось,
можно выбрать
такой ортонормированный
базис, что
перемещение
f имеет
вид R
= АR + v
, где v
- некоторый
вектор. Если
изменить начало
координат :
R = r + u
,
R
= r
+ u
, получаем:
r
= Ar
+ v
, где v
= Au
-u
+v
=
(A - E)u
+
v
.Мы видим,
что если число
1 не является
собственным
значением
матрицы А (или,
если угодно,
оператора f*)
, то можно
выбрать u
так, что в
новой системе
координат v
= 0 . (Поскольку
матрица A
- E невырождена).
Тем самым утверждение
теоремы доказано
при n=1
и при n=2
в случае
det(A) = 1
(так как
собственные
значения
![]() суть exp(
суть exp(![]() ij)№
1 при j№2pn
).
ij)№
1 при j№2pn
).
В
случае матрицы
![]() можно добиться,
чтобы v
=
можно добиться,
чтобы v
= ![]() ,
что приводит
к скользящему
отражению
,
что приводит
к скользящему
отражению ![]() .
Для матрицы
.
Для матрицы
![]() при j№2pn получаем
v
=
при j№2pn получаем
v
= ![]() ,
и мы приходим
к винтовому
перемещению
,
и мы приходим
к винтовому
перемещению
![]() .
(При j=2pn
мы приходим
к переносу).
Наконец, для
.
(При j=2pn
мы приходим
к переносу).
Наконец, для
![]() при
j№2pn
можно считать
v
= 0 , что приводит
к зеркальному
повороту
при
j№2pn
можно считать
v
= 0 , что приводит
к зеркальному
повороту ![]() ,
а при j=2pn
- v
=
,
а при j=2pn
- v
= ![]() и получается
скользящее
отражение
и получается
скользящее
отражение ![]() .
.
Замечание. ( о параметрах перемещений)
Параметр
![]() для поворота
плоскости
для поворота
плоскости
![]() будем считать
изменяющимся
mod 2p т.
е.
будем считать
изменяющимся
mod 2p т.
е. ![]() =
= ![]() .
Такое же соглашение
будем использовать
и для винтового
перемещения
.
Такое же соглашение
будем использовать
и для винтового
перемещения
![]() при
h > 0.
Если же h
= 0 , и речь идет
о повороте в
пространстве,
надо учитывать,
что
при
h > 0.
Если же h
= 0 , и речь идет
о повороте в
пространстве,
надо учитывать,
что
![]() =
= ![]() .
В частности,
.
В частности,
![]() =
= ![]() (отражение
относительно
прямой параллельной
v и проходящей
через О).
Аналогично,
(отражение
относительно
прямой параллельной
v и проходящей
через О).
Аналогично,
![]() =
= ![]() .
Если при этом j=p это
преобразование
не зависит от
вектора n и является
отражением
относительно
точки О.
.
Если при этом j=p это
преобразование
не зависит от
вектора n и является
отражением
относительно
точки О.
4* Композиции 1.
Теорема 4
Если f и g два перемещения X, а f*, g* - соответствующие операторы в V, то (f·g)* = f*g*(Символом · обозначена композиция перемещений).
Доказательство.
Используем координатную форму записи: f( R) = AR + v, g( R) = BR + w. Тогда: (f·g)( R) = f( (g( R)) = f( BR + w) = A( BR +w) +v = ( AB)R + ( Aw + v). Следовательно, (f·g)* = AB = f*g*.
Следствие.
Композиция двух перемещений с определителями одного знака имеет определитель (+1); если знаки определителей противоположны, композиция имеет определитель (-1).
Вычисление
композиции
перемещений
пространства
![]() не вызывает
затруднений.
Отметим только,
что
не вызывает
затруднений.
Отметим только,
что ![]() ·
·![]() =
= ![]() ,где v
=2AB.
,где v
=2AB.
Для
случая пространства
![]() удобно
использовать
комплексные
числа. Отождествляя
их с точками
плоскости,
получаем удобный
способ записи
перемещений.
Например, поворот
удобно
использовать
комплексные
числа. Отождествляя
их с точками
плоскости,
получаем удобный
способ записи
перемещений.
Например, поворот
![]() можно записать
в виде:
z ®
можно записать
в виде:
z ®![]() z
+ c. Точка О
является неподвижной
и соответствующее
комплексное
число
z
+ c. Точка О
является неподвижной
и соответствующее
комплексное
число ![]() находится из
уравнения
находится из
уравнения ![]() =
=
![]()
![]() + с, откуда
+ с, откуда
![]() =
с/(1-
=
с/(1-![]() ).
Таким образом,
).
Таким образом,
![]() Отметим, что
Отметим, что
![]() =
=![]() при j+y№0
(mod 2p)
. В то же время
при j+y = 0
указанная
композиция
будет переносом
на вектор AD,
где D
=
при j+y№0
(mod 2p)
. В то же время
при j+y = 0
указанная
композиция
будет переносом
на вектор AD,
где D
= ![]() .
.
Преобразование
z®![]() +c
является
скользящим
отражением
относительно
прямой Im(
+c
является
скользящим
отражением
относительно
прямой Im(![]() =
0
на вектор
0,5 (с +
=
0
на вектор
0,5 (с + ![]() ).
Если прямая
l проходит
через точку
).
Если прямая
l проходит
через точку
![]() и ее
направляющий
вектор (рассматриваемый
как комплексное
число) имеет
аргумент
и ее
направляющий
вектор (рассматриваемый
как комплексное
число) имеет
аргумент ![]() ,
то перемещение
,
то перемещение
![]() можно
записать в виде
можно
записать в виде
![]()
Композиция двух скользящих отражений относительно пересекающихся прямых будет поворотом. В то же время, если прямые параллельны, композиция - перенос.
ГРУППЫ ПРЕОБРАЗОВАНИЙ
(продолжение)
5.Кватернионы
Удобный способ аналитической записи перемещений в пространстве дают кватернионы , являющиеся обобщением комплексных чисел. Чтобы подчеркнуть аналогию между способами построения кватернионов из комплексных чисел и построением комплексных чисел из вещественных сравним обе конструкции.
Построение комплексных чисел Построение кватернионов
| 1. Комплексное число z = a + bi -это матрица | 1. Кватернион q = z + wj - это матрица |
| Отсюда вытекает, что для этих чисел имеют место те же законы действий, что и для матриц, т.е. ассоциативность умножения и закон дистрибутивности. Непосредственно проверяется коммутативность умножения комплексных чисел(но не кватернионов!) | |
| 2. Число вида a + 0i можно отождествить с вещественным числом a и таким образом | 2. Число вида z + 0j можно отождествить с комплексным числом z и таким образом |
| Модулем числа z называется вещественное число
| Модулем числа q называется вещественное число
|
| 4. Число | 4. Число |
| Обратное число определено однозначно так как ему отвечает (однозначно определенная !) обратная матрица. | |
| 5. Действия над комплексными числами, записанными в алгебраической форме производятся по обычным правилам алгебры с учетом того, что | Действия над кватернионами, записанными в виде z + wj производятся по обычным правилам алгебры с учетом того, что Таким образом, (z + wj)(z + wj) = (zz - w |
| 6. Если | 6. Если |
Связь с векторной алгеброй в ![]() .
.
В этом параграфе
нам придется
рассматривать
одновременно
несколько
разных произведений.
Крестом (ґ)
будем обозначать
векторное
произведение
в ![]() ,точкой
(Ч) - скалярное
произведение,
а звездочка
(*) будет
использована
для умножения
кватернионов.
Пусть q
=bi
+ cj +dk - чисто мнимый
кватернион.
Пользуясь
формулами
предыдущего
параграфа,
нетрудно подсчитать,
что
,точкой
(Ч) - скалярное
произведение,
а звездочка
(*) будет
использована
для умножения
кватернионов.
Пусть q
=bi
+ cj +dk - чисто мнимый
кватернион.
Пользуясь
формулами
предыдущего
параграфа,
нетрудно подсчитать,
что ![]() ,
ij
= -ji = k, jk = -kj = i, ki = - ik = j. Если
кватернионам
i , j ,k
поставить
в соответствие
правый ортонормированный
базис (i,
j, k) пространства
,
ij
= -ji = k, jk = -kj = i, ki = - ik = j. Если
кватернионам
i , j ,k
поставить
в соответствие
правый ортонормированный
базис (i,
j, k) пространства![]() ,
то чисто мнимый
кватернион
q = bi + cj +
dk можно интерпретировать
как вектор в
пространстве
и мы видим, что
умножение двух
чисто мнимых
кватернионов
сводится к
операциям
векторного
и скалярного
умножения в
,
то чисто мнимый
кватернион
q = bi + cj +
dk можно интерпретировать
как вектор в
пространстве
и мы видим, что
умножение двух
чисто мнимых
кватернионов
сводится к
операциям
векторного
и скалярного
умножения в
![]() :
q*r
= -qЧr
+ qґr
. Отсюда
следует, что
q*r
+r*q
=-2qЧr - вещественное
число, а q*r
-
r*q
=2
qґr
- чисто мнимое
число.
:
q*r
= -qЧr
+ qґr
. Отсюда
следует, что
q*r
+r*q
=-2qЧr - вещественное
число, а q*r
-
r*q
=2
qґr
- чисто мнимое
число.
Следствие
Пусть p и q - мнимые части кватернионов P и Q соответственно. Кватернионы P и Q коммутируют (то есть P*Q = Q*P ) тогда и только тогда, когда векторы p и q коллинеарны.
В
самом деле,
поскольку
вещественные
числа коммутируют
с любым кватернионом,
P*Q
= Q*P ![]() p*q
=
q*p то есть -pЧq
+ pґq
= -qЧp
+ qґp
p*q
=
q*p то есть -pЧq
+ pґq
= -qЧp
+ qґp ![]() pґq
= qґp
pґq
= qґp ![]() pґq
=0.
pґq
=0.
Используя кватернионы можно вывести некоторые свойства векторного произведения.
Теорема 5.
Для любых трех векторов p , q , r имеет место равенство (pґq) ґr + (qґr) ґp + (rґp) ґq =0 (Тождество Якоби)
(pґq) ґr = (rЧp)q - (qЧr)p
Доказательство.
Поскольку qґr = q*r + qЧr, имеем: (pґq) ґr=(pґq)*r +(pґq)Чr = (p*q) *r + (pЧq)r + (pґq)Чr ; последнее слагаемое - смешанное произведение (pqr). Производя круговую перестановку, получим: (qґr)ґp = (q*r)*p + (qЧr)p + (pqr).Сложим эти формулы и учтем ассоциативность умножения кватернионов: (pґq) ґr + (qґr)ґp = (p*(q*r)) + (q*r)*p) + (pЧq)r + (qЧr)p + 2(pqr). (1) Заменяя обратно q*r = - qЧr + qґr, преобразуем первую скобку A = -2 (qЧr)p + [p*(qґr) + (qґr)*p]. В квадратной скобке стоит произведение чисто мнимых кватернионов и потому она будет вещественным числом. Учитывая, что левая часть формулы (1) - чисто мнимое число, получаем окончательно: (pґq) ґr + (qґr)ґp = (pЧq)r - (qЧr)p. Производя круговые перестановки, получаем 2 аналогичных равенства:
(qґr) ґp + (rґp)ґq = (qЧr)p - (rЧp)q (2)
(rґp) ґq + (pґq)ґr = (rЧp)q - (pЧq)r. Складывая все 3 равенства, получаем тождество Якоби: (pґq) ґr + (qґr) ґp + (rґp) ґq =0 Вычитая из этого тождества равенство (2) , получим: (pґq) ґr = (rЧp)q - (qЧr)p.
Связь с перемещениями в ![]() .
.
Пусть p
- чисто мнимый
кватернион,
а s№0
- любой кватернион.
Пусть q
= ![]() .
Тогда
.
Тогда ![]() .
Учитывая, что
.
Учитывая, что
![]() и
и ![]() ,
получаем
,
получаем ![]() ,
то есть этот
кватернион
чисто мнимый.
Таким образом
возникает
отображение
,
то есть этот
кватернион
чисто мнимый.
Таким образом
возникает
отображение
![]() :
: ![]() .Заметим,
что
.Заметим,
что ![]() Поскольку
Поскольку ![]() ,
,
![]() - линейный оператор,
сохраняющий
скалярное
произведение.
- линейный оператор,
сохраняющий
скалярное
произведение.
Теорема 6.
Det(![]() )
= 1.
)
= 1.
Доказательство.
Пусть
e = (i,j,k).
Тогда ![]() =
(
=
(![]() )
и Det(
)
и Det(![]() )
равен определителю
этой матрицы
то есть смешанному
произведению
ее столбцов
. Имеем:
)
равен определителю
этой матрицы
то есть смешанному
произведению
ее столбцов
. Имеем:
![]() =
=
![]() +
+![]() .
Второе слагаемое
равно 0 так как
.
Второе слагаемое
равно 0 так как
![]() =0,
а первое преобразуется
следующим
образом:
=0,
а первое преобразуется
следующим
образом: ![]() =
=
![]() .
Поэтому, (
.
Поэтому, (![]() )=
)=![]() =1.
=1.
Как
нам известно,
ортогональная
матрица с
определителем
1 задает поворот
в ![]() .
Вектор v
параллельный
оси вращения
удовлетворяет
условию
.
Вектор v
параллельный
оси вращения
удовлетворяет
условию
![]() (
v )=v
Интерпретируя
v как
чисто мнимый
кватернион,
заметим, что
условие
(
v )=v
Интерпретируя
v как
чисто мнимый
кватернион,
заметим, что
условие ![]() означает, что
v и
s коммутируют.
Значит, если
Im(s) №0,
v =
lIm(s).Подсчитаем
теперь угол
поворота j.
Пусть s
= a + v, где v№0.
Пусть вектор
p
ортогонален
оси вращения
v.
Тогда v*p
=vґp
.Имеем:
означает, что
v и
s коммутируют.
Значит, если
Im(s) №0,
v =
lIm(s).Подсчитаем
теперь угол
поворота j.
Пусть s
= a + v, где v№0.
Пусть вектор
p
ортогонален
оси вращения
v.
Тогда v*p
=vґp
.Имеем: ![]() = (a - v)
p(a
+ v)
=
= (a - v)
p(a
+ v)
= ![]() +
2apґv
- (vґp)ґv.
Используя
формулы предыдущего
параграфа,
получаем:
(vґp)ґv
=
+
2apґv
- (vґp)ґv.
Используя
формулы предыдущего
параграфа,
получаем:
(vґp)ґv
= ![]() .
Итак,
.
Итак, ![]() =
= 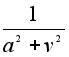 (
(![]() )
Второе слагаемое
в скобке можно
записать как
)
Второе слагаемое
в скобке можно
записать как
![]() .
Значит, cosj
=
.
Значит, cosj
= 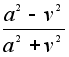 ,
sinj
=
,
sinj
=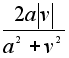 .Если
определить
угол y =
arccos(
.Если
определить
угол y =
arccos(![]() ),
то j = 2y
+2pn.
Таким образом,
поворот на
угол
),
то j = 2y
+2pn.
Таким образом,
поворот на
угол![]() вокруг
оси, заданной
единичным
вектором n
задается
формулой
вокруг
оси, заданной
единичным
вектором n
задается
формулой ![]() ,
где s
= cos(j/2)
+ n
sin(j/2).
Композиция
двух поворотов
,
где s
= cos(j/2)
+ n
sin(j/2).
Композиция
двух поворотов
![]() ,
заданных
кватернионами
s и
t = cos(a/2)
+ m
sin(a/2)
задается
формулой
,
заданных
кватернионами
s и
t = cos(a/2)
+ m
sin(a/2)
задается
формулой![]() и, следовательно,
равна
и, следовательно,
равна ![]() .
Находим:
s*t
= cos(j/2)
cos(a/2)-(nЧm)
sin(j/2)
sin(a/2)
+ n
sin(j/2)
cos(a/2)
+ m
cos(j/2)
sin(a/2)
+ (nґm)
sin(j/2)
sin(a/2).
Вещественная
часть этого
кватерниона
равна косинусу
половины угла
поворота, а
мнимая часть
определяет
направление
оси вращения.
.
Находим:
s*t
= cos(j/2)
cos(a/2)-(nЧm)
sin(j/2)
sin(a/2)
+ n
sin(j/2)
cos(a/2)
+ m
cos(j/2)
sin(a/2)
+ (nґm)
sin(j/2)
sin(a/2).
Вещественная
часть этого
кватерниона
равна косинусу
половины угла
поворота, а
мнимая часть
определяет
направление
оси вращения.
Преобразование
![]() является зеркальным
поворотом.
Особо отметим
случай вещественного
s
. В этом случае
оно имеет вид:
является зеркальным
поворотом.
Особо отметим
случай вещественного
s
. В этом случае
оно имеет вид: ![]() (зеркальный
поворот на 180
градусов) и
является центральной
симметрией.
Обозначим его
буквой Z
и отметим,
что оно перестановочно
с любым оператором.
(зеркальный
поворот на 180
градусов) и
является центральной
симметрией.
Обозначим его
буквой Z
и отметим,
что оно перестановочно
с любым оператором.
Переходя
к перемещениям
мы видим, что
формула ![]() ,
где как и выше
s = cos(j/2)
+ n
sin(j/2)
задает поворот
на угол j
вокруг оси,
заданной единичным
вектором n
и точкой
,
где как и выше
s = cos(j/2)
+ n
sin(j/2)
задает поворот
на угол j
вокруг оси,
заданной единичным
вектором n
и точкой ![]() ,
а та же формула
со знаком (-) задает
зеркальный
поворот.
,
а та же формула
со знаком (-) задает
зеркальный
поворот.
Перемещение как произведение отражений.
Теорема 7
Всякое ортогональное преобразование n- мерного векторного пространства можно представить в виде композиции не более чем n отражений.
Всякое перемещение n - мерного точечного пространства можно представить в виде композиции не более чем (n+1) отражений.
Доказательство.
Условимся, что произведение пустого множества преобразований является тождественным отображением. Приняв это соглашение, мы видим, что при n = 1 первое утверждение очевидно. При n = 2 для доказательства того же утверждения достаточно заметить, что композиция двух отражений относительно осей, составляющих угол a/2, будет вращением на угол a. Таким же образом пространственное вращение представляется в виде композиции двух отражений относительно плоскостей, проходящих через ось вращения. Наконец, зеркальный поворот требует еще одного дополнительного отражения относительно плоскости перпендикулярной оси.
Для
доказательства
второго утверждения
отметим прежде
всего, что перенос
(скажем на плоскости)
на вектор h
можно представить
в виде композиции
двух отражений
относительно
параллельных
осей, перпендикулярных
h.
Поскольку
всякое перемещение
можно рассматривать
как композицию
перемещения,
сохраняющего
начало координат(которое
можно отождествить
с соответствующим
ортогональным
оператором)
и параллельного
переноса, второе
утверждение
доказано для
всех таких
перемещений,
для которых
соответствующая
матрица представляется
в виде композиции
1.
Тогда правая
часть последнего
равенства -
число a
между 1 и 2 (1Јa1.
Но, поскольку
![]() ,
каждое слагаемое
слева не меньше
1/2. Поэтому, 4 или
больше слагаемых
слева быть не
может. Итак, k
=2 или k
=3. Если k
=2 , то
,
каждое слагаемое
слева не меньше
1/2. Поэтому, 4 или
больше слагаемых
слева быть не
может. Итак, k
=2 или k
=3. Если k
=2 , то ![]() или
или ![]() ,
откуда
,
откуда ![]() .
Два полюса (на
одной оси!)
порядка N
соответствуют
случаю группы
.
Два полюса (на
одной оси!)
порядка N
соответствуют
случаю группы
![]() .
Пусть теперь
k = 3.
Соотношение
принимает вид:
.
Пусть теперь
k = 3.
Соотношение
принимает вид: ![]() .
Пусть
.
Пусть ![]() .
Если
.
Если ![]() ,
то сумма слева
меньше 1, что
невозможно.
Значит,
,
то сумма слева
меньше 1, что
невозможно.
Значит, ![]() и равенство
принимает вид:
и равенство
принимает вид: ![]() .
Если
.
Если ![]() ,
то сумма не
больше 1/2, что
невозможно.
Итак,
,
то сумма не
больше 1/2, что
невозможно.
Итак, ![]() или =3. Если
или =3. Если ![]() ,
то
,
то ![]() .
Это случай
группы
.
Это случай
группы ![]() .
Пусть, наконец,
.
Пусть, наконец,
![]() .
Имеем:
.
Имеем: ![]() ,
откуда
,
откуда
![]() .
Для
.
Для ![]() находим N
= 12, что соответствует
случаю группы
T.
Для
находим N
= 12, что соответствует
случаю группы
T.
Для ![]() получаем N
= 24 - случай
группы W,
Наконец при
получаем N
= 24 - случай
группы W,
Наконец при
![]() - N = 60 и
мы приходим
к группе P.
- N = 60 и
мы приходим
к группе P.
16.Пространственные группы, содержащие зеркальные отражения.
Пусть
S конечная
группа перемещений
в пространстве
содержащая
преобразования
с определителем
(-1). По теореме
12 такая группа
содержит 2n
элементов
![]() ,
причем первые
n ее
элементов имеют
определитель
1 и составляют
подгруппу
G=G(S)
, а последние
n имеют
определитель
(-1) и получаются
из элементов
подгруппы путем
их умножения
на любой фиксированный
элемент g
с определителем
(-1):
,
причем первые
n ее
элементов имеют
определитель
1 и составляют
подгруппу
G=G(S)
, а последние
n имеют
определитель
(-1) и получаются
из элементов
подгруппы путем
их умножения
на любой фиксированный
элемент g
с определителем
(-1): ![]() Напомним, что
буквой Z
была обозначена
симметрия
относительно
начала координат
(зеркальный
поворот на p).
Это перемещение
перестановочно
с любым другим
и
Напомним, что
буквой Z
была обозначена
симметрия
относительно
начала координат
(зеркальный
поворот на p).
Это перемещение
перестановочно
с любым другим
и ![]() .
.
Теорема 17.
Пусть
S конечная
группа перемещений
в пространстве
и ![]() .
Если G(S)
= {
.
Если G(S)
= {![]() },
то S = {
},
то S = {![]()
![]() }.
}.
Доказательство.
Теорема очевидна, так как det(Z) = -1.
Замечание.
Группа
S в этом
случае обозначается
![]()
Теорема 18.
Пусть
S конечная
группа перемещений
в пространстве
и ![]() .
Если G(S)
= {
.
Если G(S)
= {![]() },
то множество
},
то множество
![]() является группой
является группой
![]() -
преобразований
. Обратно, если
Г любая группа
вращений из
2n элементов,
содержащая
G,
то, домножая
все элементы
из Г-G
на Z,
получаем группу
перемещений
S, для которой
G(S)
= G.
-
преобразований
. Обратно, если
Г любая группа
вращений из
2n элементов,
содержащая
G,
то, домножая
все элементы
из Г-G
на Z,
получаем группу
перемещений
S, для которой
G(S)
= G.
Доказательство.
Надо
проверить, что
![]() и
и
![]() .
Если
.
Если ![]() ,
то эти условия
выполнены
поскольку G
- группа
преобразований.
Если
,
то эти условия
выполнены
поскольку G
- группа
преобразований.
Если ![]() ,то
ни один из элементов
,то
ни один из элементов
![]() не входит в G
и потому это
множество
совпадает с
множеством
{
не входит в G
и потому это
множество
совпадает с
множеством
{
![]() }.
Поэтому
}.
Поэтому ![]()
![]() .
Аналогично,
поскольку ни
один из элементов
.
Аналогично,
поскольку ни
один из элементов
![]() не входит в G,
все произведения
не входит в G,
все произведения
![]() и потому
и потому ![]()
![]() .
Таким же образом
убеждаемся,
что
.
Таким же образом
убеждаемся,
что ![]() и, значит,
и, значит, ![]()
![]() .
Обратное утверждение
теоремы проверяется
точно таким
же образом.
.
Обратное утверждение
теоремы проверяется
точно таким
же образом.
Замечание.
Стандартное
обозначение
для S в
этом случае
- ![]() .
.
Следствие.
Конечная группа перемещений пространства, содержащая зеркальные вращения совпадает с одной из групп ( в скобках указаны их порядки):
![]() (2n),
(2n), ![]() (4n),
(4n), ![]() (24),
(24), ![]() (48),
(48), ![]() (120);
(120);
![]() (2n),
(2n), ![]() (2n),
(2n), ![]() (4n),
(4n), ![]() (24).
(24).
Замечание 1.
Полные группы симметрий правильных многогранников получаются по способу, указанному в теореме 17, если этот многогранник имеет центр симметрии. В противном случае используется конструкция теоремы 18.
Следовательно, это следующие группы:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Замечание 2.
Назовем флагом
многогранника
тройку (D,
R, v), где D-
некоторая его
грань, R
- одно из ребер,
ограничивающих
эту грань и v
- вершина,
лежащая на этом
ребре. Многогранник
называется
правильным
(это одно из
возможных
определений
), если для любых
двух его флагов
![]() и
и ![]() существует
перемещение,
переводящее
многогранник
в себя и отображающее
первый флаг
во второй. Поскольку
перемещение
оставляющее
флаг неподвижным
очевидно является
тождественным,
мы видим, что
порядок группы
G правильного
многогранника
совпадает с
количеством
его флагов.
Таким образом,
существует
перемещение,
переводящее
многогранник
в себя и отображающее
первый флаг
во второй. Поскольку
перемещение
оставляющее
флаг неподвижным
очевидно является
тождественным,
мы видим, что
порядок группы
G правильного
многогранника
совпадает с
количеством
его флагов.
Таким образом,
![]() =2Гr,
где Г - количество
его граней, r
- количество
ребер, ограничивающих
некоторую
грань, 2 - количество
вершин на р
=2Гr,
где Г - количество
его граней, r
- количество
ребер, ограничивающих
некоторую
грань, 2 - количество
вершин на р
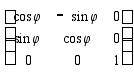
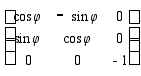
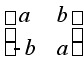 , где
, где 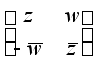 , где
, где
0 комментариев