Концептуальная постановка задачи

2. Концептуальная постановка задачи

2.1. Геометрические элементы трамплинов

Трамплины создаются под определенную дальность полета прыгунов, которую вычисляют как расстояние от точки старта до точки приземления по склону. Трамплины делятся по дальности на 5 категорий:

маленькие трамплины 20-45 м

средние трамплины 50-70 м

нормальные трамплины 75-90 м

большие трамплины 105-120 м

трамплины для полетов 145-185 м

Соревнования в России проводятся, как правило, на больших трамплинах, а международные соревнования - на трамплинах для полетов. Для того, чтобы лыжник, идущий на рекорд, не разбился, улетев за пределы склона приземления или недолетев до него, существуют специальные формулы и нормы для расчета геометрических параметров трамплинов.

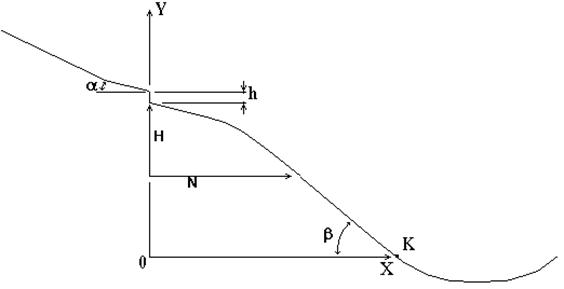
Рис. 1. Основные геометрические элементы трамплина

Трамплин состоит из участка для разгона и так называемого стола отрыва, с которого лыжники уходят в свободный полет. Стол отрыва наклонен к горизонтали под небольшим отрицательным углом, обычно от -6О до -12О. Здесь собственно трамплин заканчивается, а все, что дальше, называется горой приземления или трамплинной горой. Высота стола отрыва над склоном горы приземления обычно обозначается  и составляет от 2% до 4% от максимальной дальности, обозначаемой . Трамплинная гора состоит из трех участков: участка необработанного склона длиной  и шириной , участка приземления - прямого участка склона, составляющего с горизонталью отрицательный угол , равный согласно принятым нормам от -25О до -40О, и участка торможения. Участок торможения как правило имеет профиль, плавно закругляющийся вверх. Расстояние по горизонтали от канта отрыва - крайней точки стола отрыва - до точки максимальной дальности обозначается . Этой буквой обозначается также критическая точка - конец участка приземления.

2.2. Собственно концептуальная постановка

Кратко цель данной работы звучит так: "как прыгнуть, чтобы улететь подальше и не разбиться?" Изменяя свою позицию во время отрыва, относительное положение ног, рук и корпуса, атлет может контролировать траекторию своего полета в воздухе, управляя углом атаки. Задача формулируется следующим образом: как должен лыжник управлять своим телом, чтобы приземлиться настолько далеко, насколько возможно, и при этом иметь приемлемую посадочную скорость.

Если старт и полет проходят нормально, то практически невозможно приземлиться раньше начала склона приземления. Но существует другая опасность. Лыжник оканчивает полет с большой скоростью, которую необходимо погасить. Для этого существует слегка закругляющийся участок торможения. Но если прыгун перелетает критическую точку, то он серьезно рискует, так как дальше склон закругляется вверх, и угол, под которым его траектория подходит к склону, будет составлять уже не 5-10О, а значительно больше. Поэтому приземление ральше или позже специально созданного для этого участка приземления в первом случае невозможно, а во втором - недопустимо. Параллельная склону составляющая скорости гасится при дальнейшем движении лыжника по зкругленному склону. Наибольшую опасность при приземлении представляет собой составляющая скорости, перпендикулярная склону, так как при слишком большой нормальной скорости кроме больших ударных нагрузок также есть риск упасть - при том, что в момент приземления лыжник имеет скорость в несколько десятков км/ч. Поэтому нормальная к склону составляющая посадочной скорости не должна превышать 7 м/с, а желательно должна составлять 3-5 м/с.

3. Математическая постановка задачи

3.1. Предположения

Ось абсцисс направлена в сторону полета лыжников параллельно горизонту, ось ординат - вверх через край стола отрыва, называемый кантом отрыва. Начало координат расположено так, что абсцисса точки старта и ордината критической точки  - конца участка приземления - равны нулю. Если нет бокового ветра и других возмущений, центр масс лыжника описывает кривую в вертикальной плоскости, то есть задачу полета можно рассматривать как двухмерную.

Очевидно, прыгун может изменять свои аэродинамические параметры, на которые влияют следующие факторы:

кинетический момент системы прыгун-лыжи относительно оси, перпендирулярной плоскости рисунка и проходящей через центр масс системы, в момент отрыва и в полете;

изменение момента инерции системы относительно той же оси в полете;

различные активные и реактивные эффекты, связанные с вращением различных частей тела вследствие работы мышц.

Результаты многих исследований кинограмм [1, 5] доказывают относительную статичность положения каждого прыгуна в полете. Это упрощает описание картины перемещений и скоростей системы прыгун-лыжи и позволяет использовать индивидуальные экспериментальные характеристики, получаемые в аэродинамической трубе. Благодаря этому было введено предположение о неизменности позы лыжника в полете.

Весь прыжок можно разбить на четыре фазы: взлет, группировку, собственно полет и подготовку к приземлению. Первая фаза длится примерно 0.3 с, вторая -0.8-0.9 с, третья - 0.3-0.6 с. Все остальное время поза лыжника практически не меняется - см. рис.2 [1].

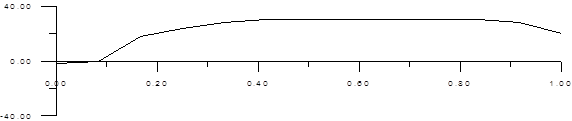
Рис. 2. Изменение угла атаки прыгуна во время прыжка

(по оси абсцисс отложено отношение текущей дальности к полной дальности прыжка, по оси ординат - угол атаки туловища в градусах по результатам среднего прыжка).

Таким образом, в основной фазе полет прыгуна близок к поступательному движению, что делает естественным предположение о замене рассмотрения прыгуна рассмотрением движения его центра масс.

Похожие работы

Задача о движении снаряда

Скачать

11197

1

9

... . Однако все это вполне можно сделать на компьютере, построив предварительно математические модели изучаемых явлений. Целью данной курсовой работы является моделирование движения снаряда. модель параметр движение снаряд Постановка задачи   Снаряд пущен с Земли с начальной скоростью v0 под углом  к ее поверхности; требуется найти траекторию его движения (y), расстояние S между ...