Вариант 1.
1. Для матричной игры, заданной платёжной матрицей A, найти:
все максиминные стратегии игрока 1;
все минимаксные стратегии игрока 2;
все седловые точки;
цену игры.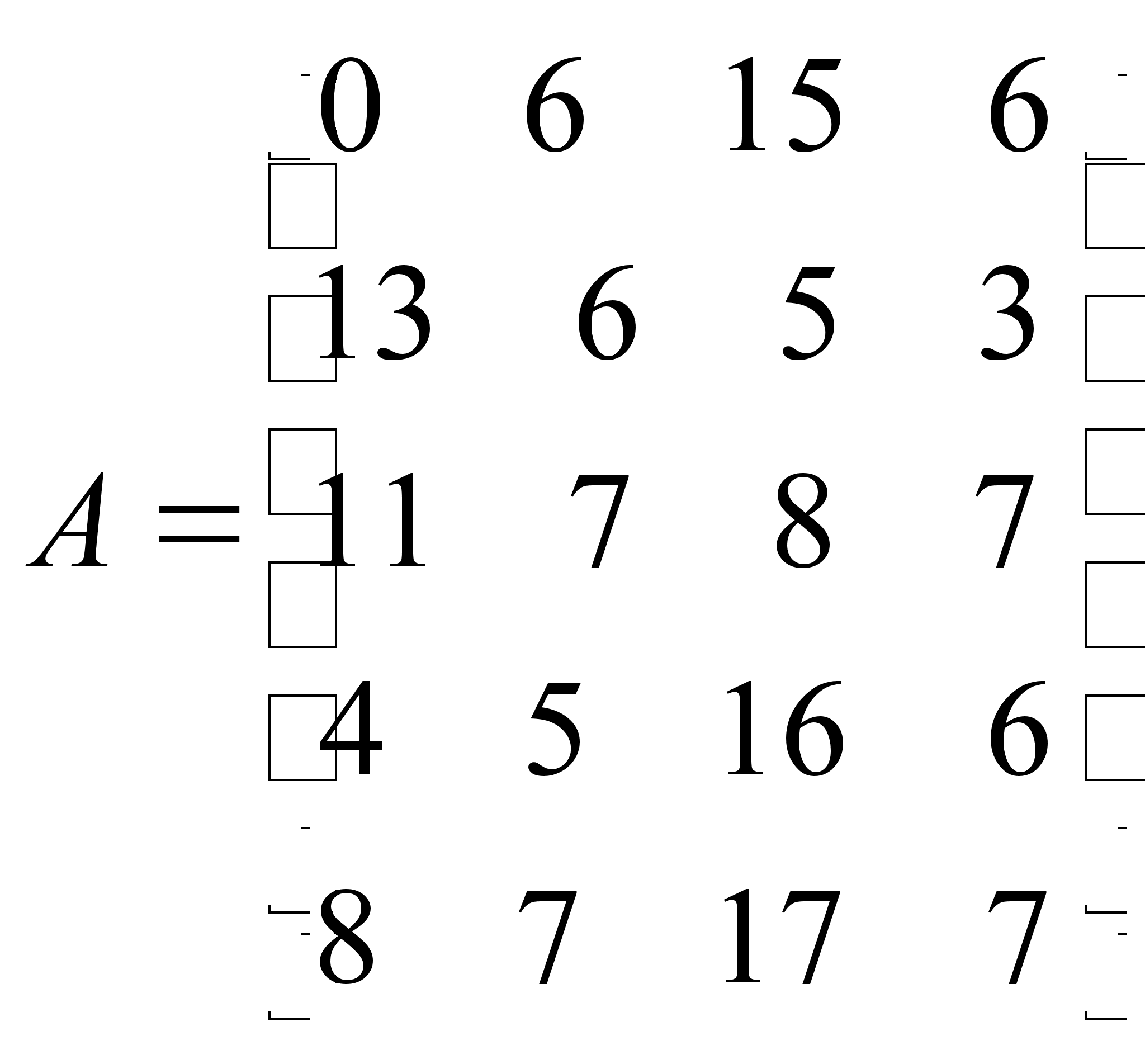
Решение
Максиминные стратегии игрока 1 определяются по формуле:
![]()
Для
строк таблицы
получаем следующие
значения ![]() :
:
(0, 3, 7, 4, 7). Максимумов два: для 3-й строки и для 5-й. Они равны 7. Таким образом, игрок 1 имеет две максиминные стратегии: 3 и 5.
Минимаксные стратегии игрока 2 ищутся по формуле:
![]()
Для
столбцов таблицы
получаем такие
значения ![]() :
:
(13, 7, 17, 7).
Игрок 2 имеет две минимаксные стратегии: 2 и 4.
Седловых точек четыре: (3,2); (5,2); (3,4); (5,4).
Первая цифра в скобках – номер выбранной стратегии для игрока 1, вторая – для игрока 2.
Цена игры равна 7.
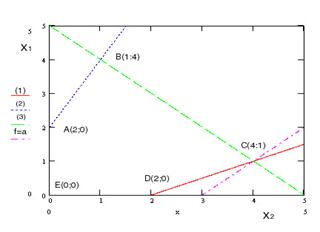
2. Найти решение матричной игры аналитическим методом, комбинируя его с отбрасыванием доминируемых стратегий:
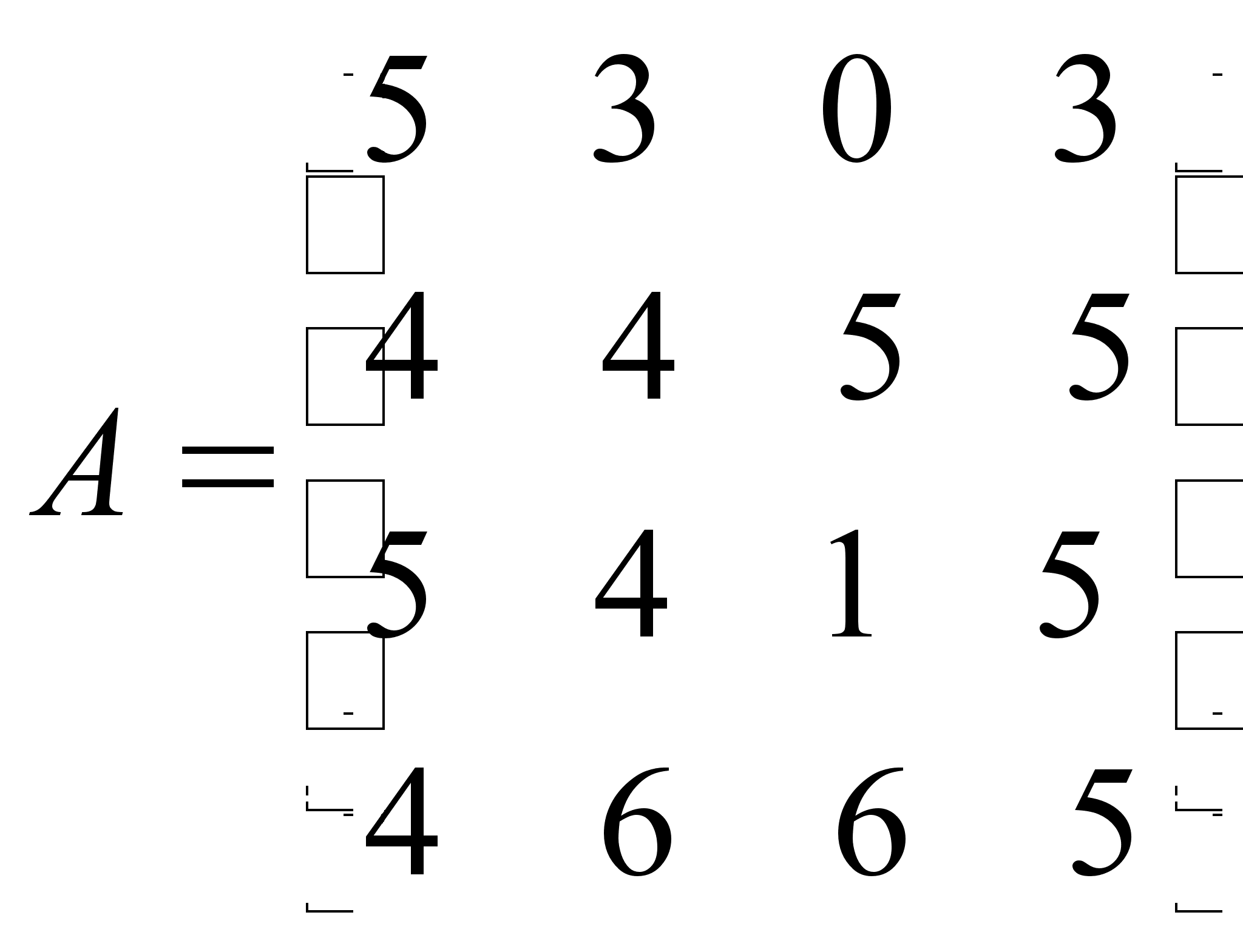
Решение
Доминирующей называется такая стратегия, которая во всех случаях по крайней мере не хуже, а в некоторых и лучше, чем другая. Вторая стратегия в этом случае называется доминируемой и может быть отброшена.
Для игрока 1 стратегия 1 доминируется стратегией 3, а стратегия 2 доминируется стратегией 4. Таким образом, стратегии 1 и 2 могут быть отброшены, получим матрицу:
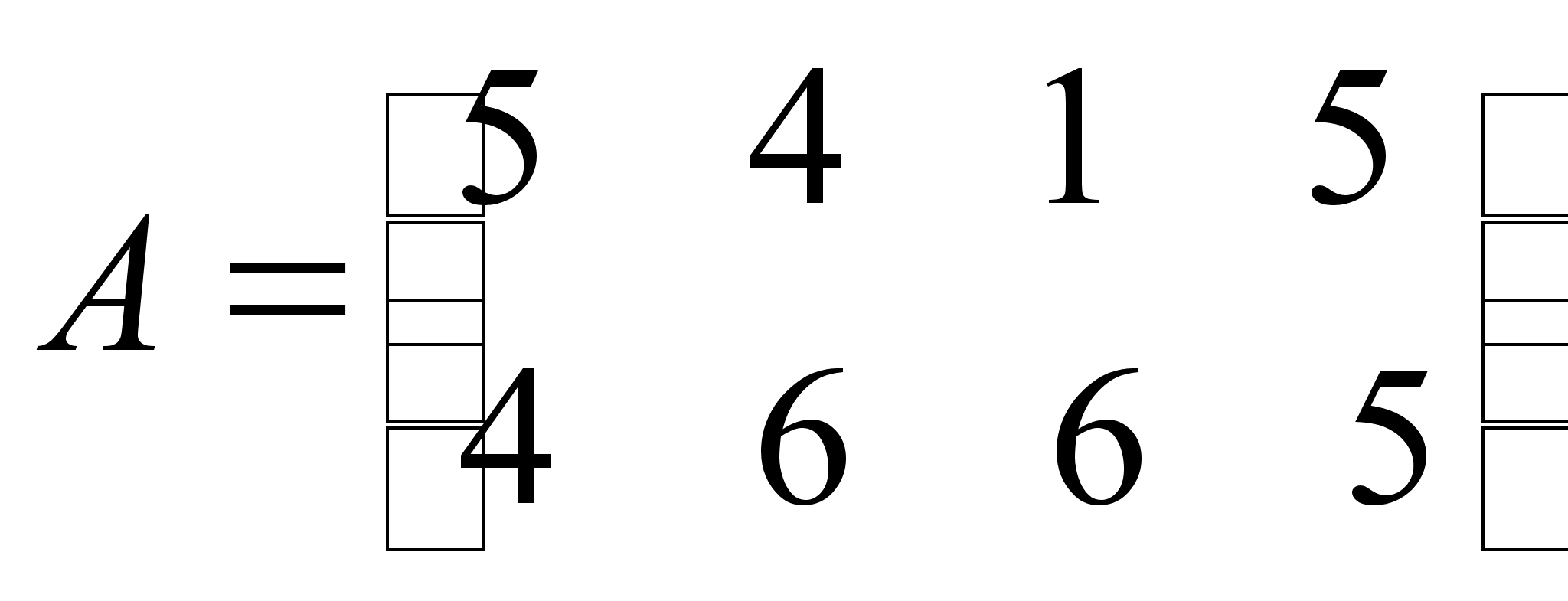
Теперь проверим стратегии игрока B. 4-й столбец доминируется 1-м, а 2-й доминируется 3-м. Отбрасываем 2-й и 4-й столбцы, получаем:
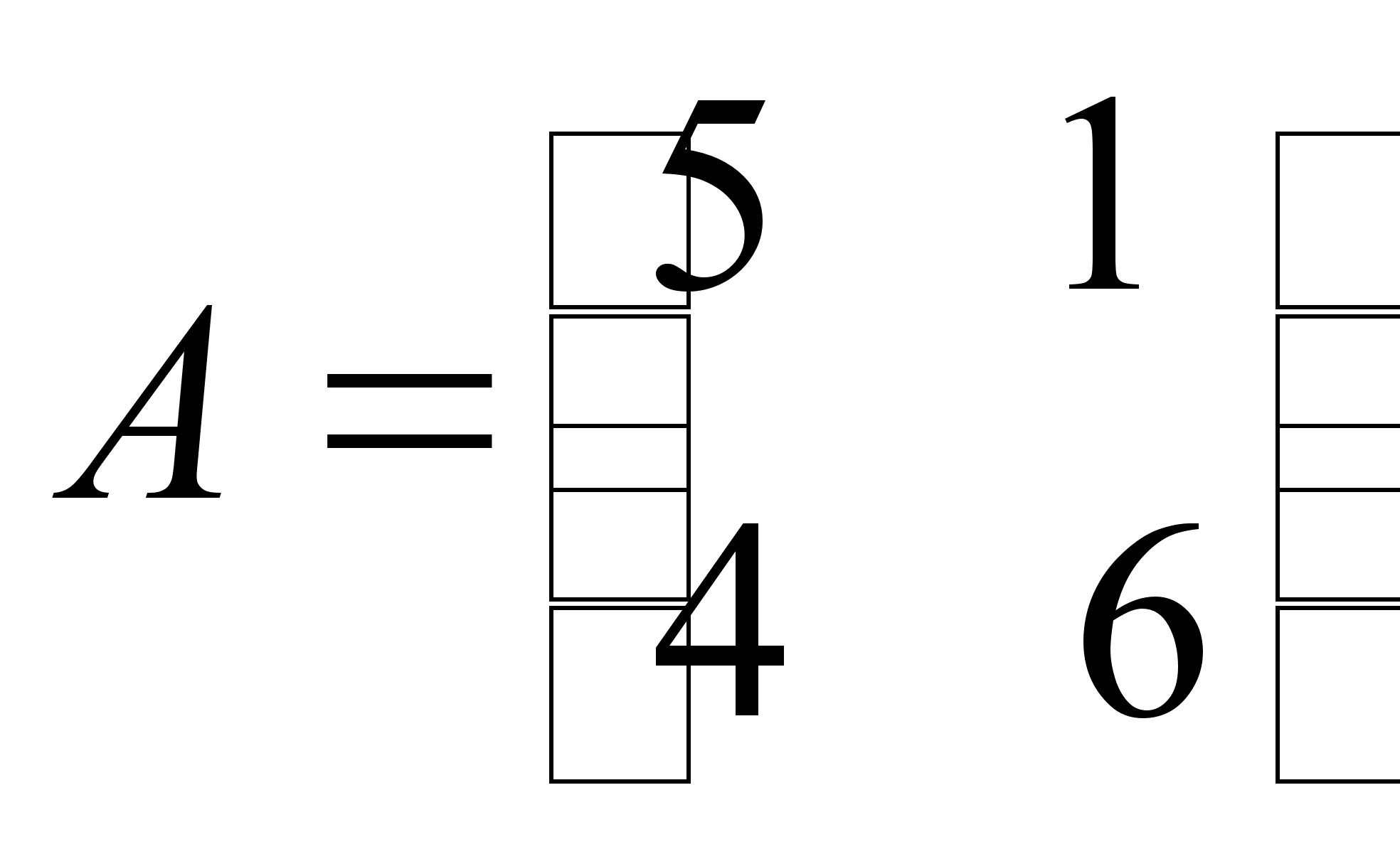
Осталась матрица 2*2. Она имеет седловую точку (2,1). Цена игры равна 4.
Таким образом, из исходных стратегий наилучшей для игрока 1 будет стратегия 4 (4-я строка исходной матрицы), а для игрока 2 – стратегия 1 (1-й столбец). Значение выигрыша игрока 1 при этом будет равно 4.
Работы на заказ 488525@mail.ru
Похожие работы
... (метод фиктивного разыгрывания) и его обоснованию. Приведён пример применения алгоритма для конкретной матричной игры. В третьем параграфе рассмотрен ещё один метод – монотонный итеративный алгоритм приближённого решения матричных игр. §1. Основные понятия Будем рассматривать только парные антагонистические игры, т. е. игры в ...
... R:=maximize(f,C ,NONNEGATIVE ); Ø f_max:=subs(R,f); Ø R1:=minimize(f,C ,NONNEGATIVE ); f_min:=subs(R1,f); ОТВЕТ: При x1=5/4 x2=5/4 f_max=15/4; При x1=0 x2=0 f_min=0; Урок № 5.Решение матричных игр, используя методы линейного программирования и симплекс метод Тип урока: урок контроль + урок изучения нового материала. Вид урока: Лекция. Продолжительность: ...
... Тройка является решением игры <=>, когда является решением игры , где а – любое вещественное число, к>0 ГЛАВА 2. Игры с нулевой суммой в чистых стратегиях 2.1 Вычисление оптимальных стратегий на примере решения задач Используя теорему о минимаксе, можно утверждать, что каждая антагонистическая игра имеет оптимальные стратегии. Теорема: пусть А – матричная игра и строки данной ...
... смешанными стратегиями игроков 1 и 2 называются такие наборы хо, уо соответственно, которые удовлетворяют равенству Е (А, х, y) = Е (А, х, y) = Е (А, хо, уо). Величина Е (А, хо ,уо) называется при этом ценой игры и обозначается через u. Имеется и другое определение оптимальных смешанных стратегий: хо, уо называются оптимальными смешанными стратегиями соответственно игроков 1 и 2, если они ...
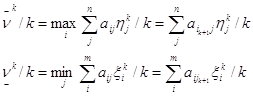
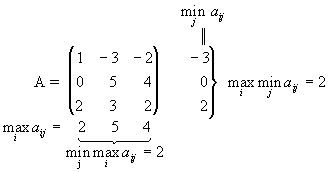
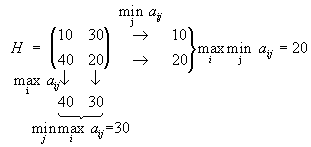
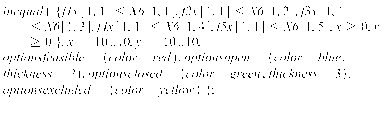
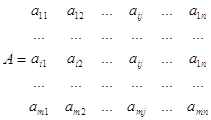
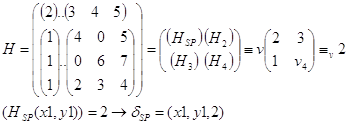
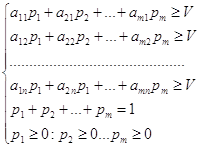
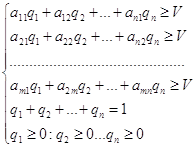
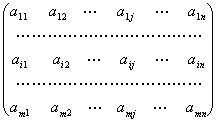
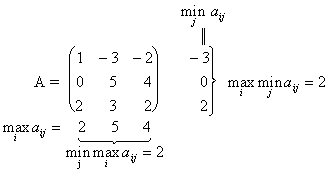
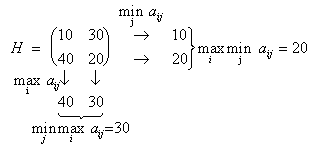
0 комментариев