Министерство рыбного хозяйства
Владивостокский морской колледж
|
|
ТЕМА: “ Системы 2-х , 3-х линейных уравнений.
Правило Крамера. ”
г. Владивосток
ОГЛАВЛЕНИЕ.
1.Краткая теория .
2. Методические рекомендации по выполнению заданий.
3.Примеры выполнения заданий.
4.Варианты заданий.
5.Список литературы.
1. КРАТКАЯ ТЕОРИЯ .
________________________________
Пусть дана система линейных уравнений
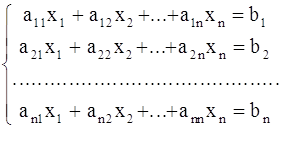 (1)
(1)
Коэффициенты a11,12,..., a1n, ... , an1 , b2 , ... , bn считаются заданными .
Вектор -строка íx1 , x2 , ... , xn ý - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.
Определитель n-го порядка D=çAê=ça ij ç, составленный из коэффициентов при неизвестных , называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи.
a). Если D¹0, то система (1) имеет единственное решение, которое может быть найдено по формулам Крамера : x1=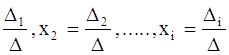 , где
, где
определитель n-го порядка Di ( i=1,2,...,n) получается из определителя системы путем замены i-го столбца свободными членами b1 , b2 ,..., bn.
б). Если D=0 , то система (1) либо имеет бесконечное множество решений , либо несовместна ,т.е. решений нет.
2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
__________________________________________
1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.
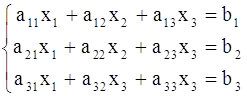 (2).
(2).
1. В данной системе составим определитель 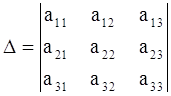 и вычислим.
и вычислим.
2. Составить и вычислить следующие определители :
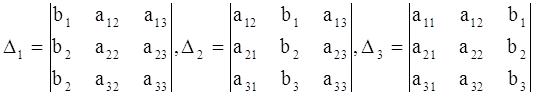 .
.
3. Воспользоваться формулами Крамера.
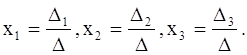
3. ПРИМЕРЫ.
_______________
1. 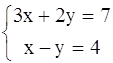 .
.
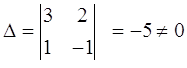
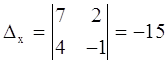
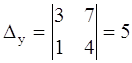
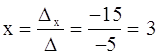
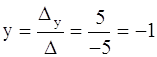 .
.
Проверка:
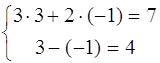 Ответ:
( 3 ; -1 ).
Ответ:
( 3 ; -1 ).
2. 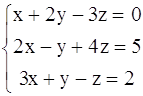
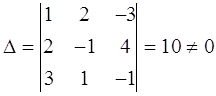
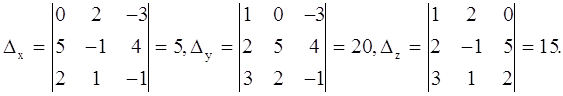
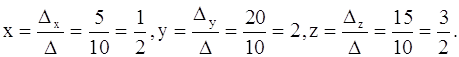
Проверка:
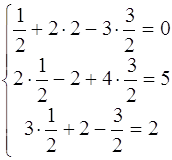
Ответ: x=0,5 ; y=2 ; z=1,5 .
4. ВАРИАНТЫ ЗАДАНИЙ.
___________________________
ВАРИАНТ 1.
Решить системы:
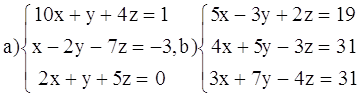
ВАРИАНТ 2.
Решить системы:
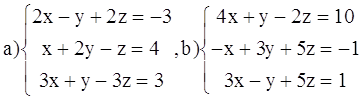
ВАРИАНТ 3.
Решить системы:
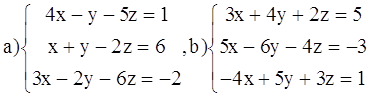
ВАРИАНТ 4.
Решить системы:
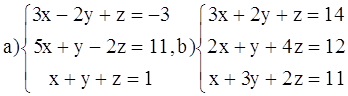
ВАРИАНТ 5.
Решить системы:
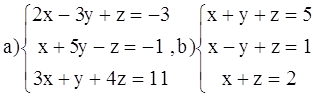
ВАРИАНТ 6.
Решить системы:
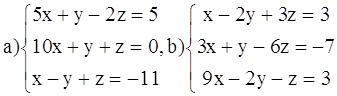
ВАРИАНТ 7.
Решить системы:
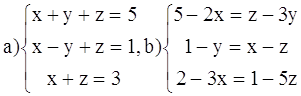
ВАРИАНТ 8.
Решить системы:

1. Г.И. КРУЧКОВИЧ.
“Сборник задач по курсу высшей математике.”
М. “Высшая школа”, 1973 год.
2. В.С. ШИПАЧЕВ.
“Высшая математика.”
М. “Высшая школа”, 1985 год.
Похожие работы
... . При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений. К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над ...
... вычисляют в следующем порядке: xjn, xjn–1, …, xj1. 3. Метод Зейделя 3.2.1. Приведение системы к виду, удобному для итераций. Для того чтобы применить метод Зейделя к решению системы линейных алгебраических уравнений Ax = b с квадратной невырожденной матрицей A, необходимо предварительно преобразовать эту систему к виду x = Bx + c. Здесь B – квадратная матрица с элементами bij (i, ...
... ; b x, y ≥ 0. b принимает значение 18 с вероятностью и значение 45 с вероятностью . Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 1 1) Показать результат произведения матрицы размерности m х n на вектор- ...
... Найти произведение матриц А = и В = Вычислить значение функции f (x1, x2, x3, x4) = 8 x1 x2 + 4 + 10 x1 (x4)2 в точке (1, 2, 4, 3) Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МАТЕМАТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭКОНОМИКИ Билет № 16 Объяснить связь базиса и размерности пространства. Дать основные положения задачи ...


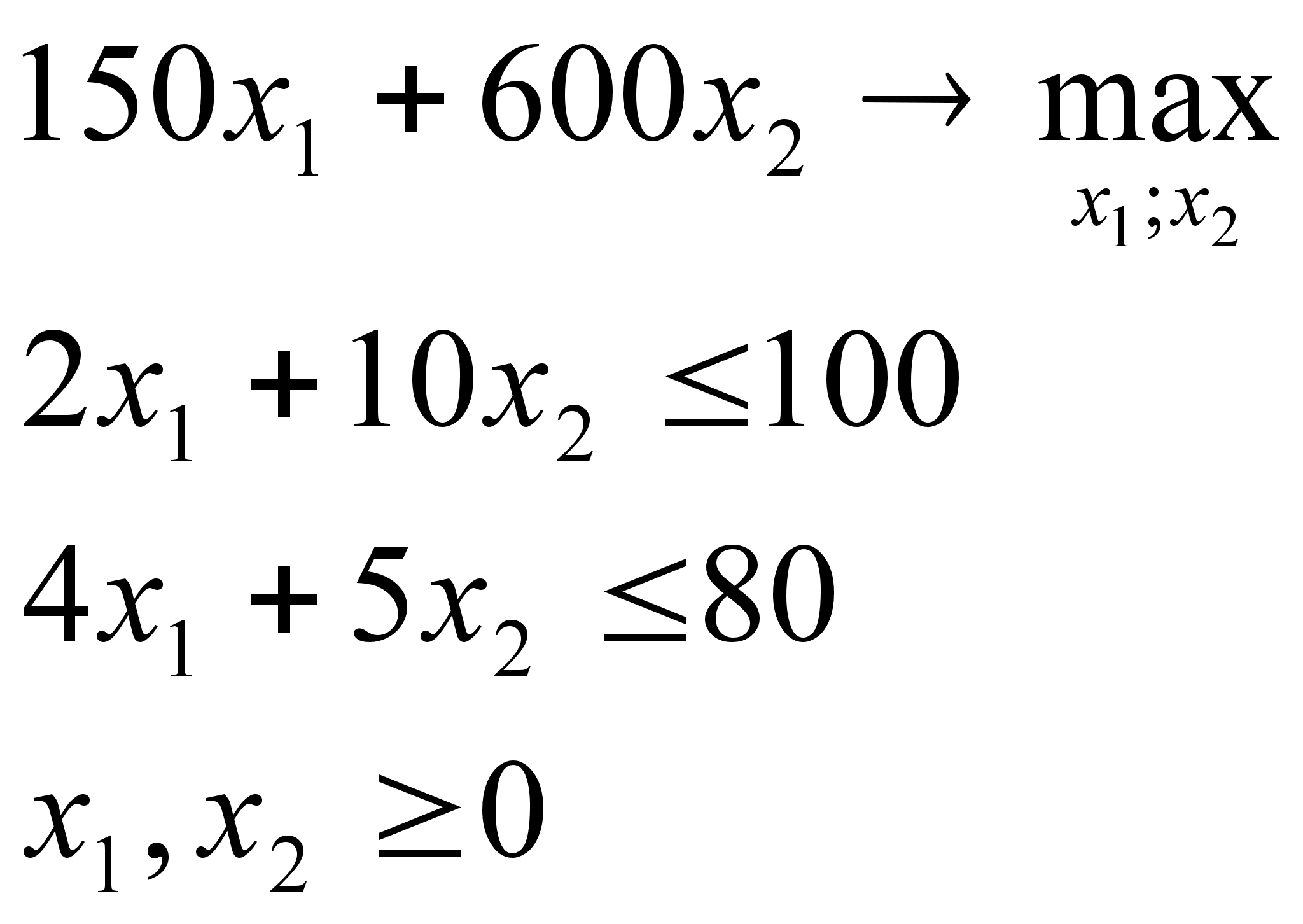
0 комментариев