Навигация
Минимизация функций нескольких переменных. Метод спуска
Министерство путей сообщения РФ
Дальневосточный государственный университет
путей сообщения
Кафедра «Прикладная математика» Курсовая работа
по численным методам
«Минимизация функций нескольких переменных.
Метод спуска.»
Выполнили: Косолапов А.Г. Терехов А.А.
Проверил: Смагин С.И.
Хабаровск 2003
Содержание:
I. Методы спуска (Общая схема) _________________________ 3
II. Метод покоординатного спуска._____________________ 4
III. Метод градиентного спуска.________________________________ 7
IV. Метод наискорейшего спуска.______________________________ 9
V. Описание программы._____________________________________10
VI. Общая блок схема.________________________________________ 11 VII. Руководство для пользования.______________________________12 VIII. Приложение А (Листинг программы)__________________________13IX. Приложение B
(Исследование функции U=A*x1^3+B*x2^2-C*x1-D*x2 (изменение шага))_____ 25
Методы спуска
Все методы спуска решения задачи безусловной минимизации различаются либо выбором направления спуска, либо способом движения вдоль направления спуска. Это позволяет написать общую схему методов спуска.
Решается задача минимизации функции j(x) на всём пространстве En. Методы спуска состоят в следующей процедуре построения последовательности {xk}. В качестве начального приближения выбирается любая точка x0ÎEn. Последовательные приближения x1, x2, … строятся по следующей схеме:
1) в точке xk выбирают направление спуска - Sk;
2) находят (k+1)-е приближение по формуле xk+1=xk-hkSk.
Направление Sk выбирают таким образом, чтобы обеспечить неравенство f(xk+1)<f(xk) по крайней мере для малых значений величины hk. На вопрос, какому из способов выбора направления спуска следует отдать предпочтение при решении конкретной задачи, однозначного ответа нет.
Число hk определяет расстояние от точки xkдо точки хk+1. Это число называется длиной шага или просто шагом. Основная задача при выборе величины hk - это обеспечить выполнение неравенства j(xk+1)<j(xk).
Величина шага сильно влияет на эффективность метода. Большей эффективностью обладает вариант метода, когда шаг по каждой переменной определяется направляющими косинусами градиента(в градиентных методах).
xk+1=xk-hk cos![]()
где - cos![]() =
=![]()
В этом случаи величина рабочего шага не зависит от величины модуля градиента, и ею легче управлять изменением h . В районе оптимума может возникать значительное «рыскание», поэтому используют различные алгоритмы коррекции h.
Наибольшее распространение получили следующие алгоритмы:
1. ![]() (без коррекции);
(без коррекции);
2. ![]() если
если ![]() ;
; ![]() если
если ![]()
3. ![]() , если
, если ![]() ;
; ![]() , если
, если![]() ;
; ![]() ,если
,если ![]() ,
,
где ![]() –угол между градиентами на предыдущем и текущем шаге;
–угол между градиентами на предыдущем и текущем шаге;
![]() и
и![]() – заданные пороговые значения выбираются субъективно
– заданные пороговые значения выбираются субъективно
(например, ![]() ).
).
Вдали от оптимума направление градиента меняется мало, поэтому шаг можно увеличить (второе выражение), вблизи от оптимума направление резко меняется (угол между градиентами R(x) большой), поэтому h сокращается (третье выражение).
Метод покоординатного спуска.
Пусть нужно найти наименьшее значение целевой функции
u=f(M)=f(x1, x2, . . . ,xn). Здесь через М обозначена точка n-мерного пространства с координатами x1, x2, . . . ,xn: M=(x1, x2, . . . ,xn). Выберем какую-нибудь начальную точку М0=(x10, x20, . . . ,xn0) и рассмотрим функцию f при фиксированных значениях всех переменных, кроме первой: f(x1, x20,x30, . . . ,xn0 ). Тогда она превратится в функцию одной переменной x1 . Изменяя эту переменную, будем двигаться от начальной точки x1=x10 в сторону убывания функции, пока не дойдем до ее минимума при x1=x11, после которого она начинает возрастать. Точку с координатами ( x11, x20,x30, . . . ,xn0) обозначим через М1, при
этом f(M0) >= f(M1).
Фиксируем теперь переменные: x1=x11, x3= x30, . . . ,xn=xn0и рассмотрим функцию f как функцию одной переменной x2: f(x11, x22, x30. . . ,xn0). Изменяя x2 , будем опять двигаться от начального значения x2=x20 в сторону убывания функции, пока не дойдем до минимума при x2=x21 .Точку с координатами
{x11, x21, x30 . . . xn0} обозначим через М2, при этом f(M1) >=f(M2).
Проведем такую же минимизацию целевой функции по переменным
x3, x4, . . . ,xn. Дойдя до переменной xn, снова вернемся к x1 и продолжим процесс. Эта процедура вполне оправдывает название метода. С ее помощью мы построим последовательность точек М0,М1,М2, . . . , которой соответствует монотонная последовательность значений функции
f(M0) >= f (M1)>= f(M2) >= Обрывая ее на некотором шаге k можно приближенно принять значение функции f(Mk) за ее наименьшее значение в рассматриваемой области.
Проведем такую же минимизацию целевой функции по переменным x3, x4, . . . ,xn. Дойдя до переменной xn, снова вернемся к x1 и продолжим процесс. Эта процедура вполне оправдывает название метода. С ее помощью мы построим последовательность точек М0,М1,М2, . . . , которой соответствует монотонная последовательность значений функции
f(M0)>= f(M1)>= f(M2) >= ... Обрывая ее на некотором шаге k можно приближенно принять значение функции f(Mk) за ее наименьшее значение в рассматриваемой области. Отметим , что данный метод сводит задачу поиска наименьшего значения функции нескольких переменных к многократному решению одномерных задач оптимизации. Если целевая функция f(x1, x2, ... ,xn) задана явной формулой и является дифференцируемой, то мы можем вычислить ее частные производные и использовать их для определения направления убывания функции по каждой переменной и поиска соответствующих одномерных минимумов. В противном случае, когда явной формулы для целевой функции нет, одномерные задачи следует решать с помощью одномерных методов
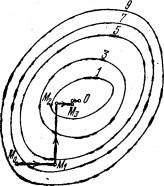
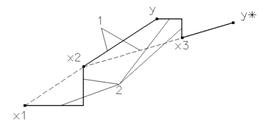
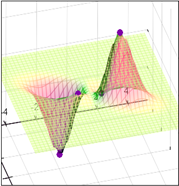
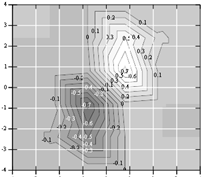
На рис.изображены линии уровня некоторой функции двух переменных u= f (х, у). Вдоль этих линий функция сохраняет постоянные значения, равные 1, 3, 5, 7, 9. Показана траектория поиска ее наименьшего значения, которое достигается в точке О, с помощью метода покоординатного спуска. При этом нужно ясно понимать, что рисунок служит только для иллюстрации метода.
Пусть требуется решить задачу (2):
f(x) ![]() min, х ÎRn. (2)
min, х ÎRn. (2)
В двумерном пространстве R2. Решение задачи (2) методом покоординатного спуска, иначе называемого методом Гаусса - Зейделя, производят по следующей общей схеме.
Выбирают произвольно начальную точку х(0) из области определения функции f(х). Приближения х(k) определяются соотношениями
(3): x(k+1)=x(k)+t(k)S(k) (k=0,1,2, ...),
где вектор направления спуска s(k)- это единичный вектор, совпадающий с каким-либо координатным направлением (например, если S(k)параллелен х1, то S(k)= {1,0,0,...,0}, если он параллелен x2, то S(k)={0, 1, 0, . . . ,0} и т.д.) ; величина t(k) является решением задачи одномерной минимизации:
f(x(k)+ts(k)) ![]() min, t ÎR1, (k=0,1,2, ...),
min, t ÎR1, (k=0,1,2, ...),
и может определяться, в частности, методом сканирования.
Детальная реализация общей схемы в двумерном случае R2дает траекторий приближения к точке х* методом покоординатного спуска, состоящую из звеньев ломаной, соединяющих точки х(k), x1~(k) x(k+1) (k=0, 1, 2,) . При k=0, исходя из начальной точки х(0)=(x1(0),x2(0)), находят точку х~(0)= (x1~(0),x2(0)), минимума функции одной переменной f(x1,x2(0)); при этом f(x~(0))<=f(x(0)).Затем находят точку минимума x(1) функции f (x1~(0),x2) по второй координате. Далее делают следующий шаг вычислений при k=1. Полагают, что исходной точкой расчета является х(1). Фиксируя вторую координату точки х(1), находят точку минимума х~(1)= (x1~(1),x2(1)), функции f(x1,x2(1)) одной переменной x(1); при этом f(x~(1))<=f(x(1))<=f(x(0)). Точку х(2) получают, минимизируя целевую функцию f(x1~(1),x2), вновь по коорданате х2, фиксируя координату x1~(1) ,точки x(1) , и т.д.
Условием прекращения вычислительной процедуры при достижении заданной точности e может служить неравенство
||x(k+1) - x(k) ||<e (4)
Блок-схема поиска минимума функции двух переменных методом покоординатного спуска.
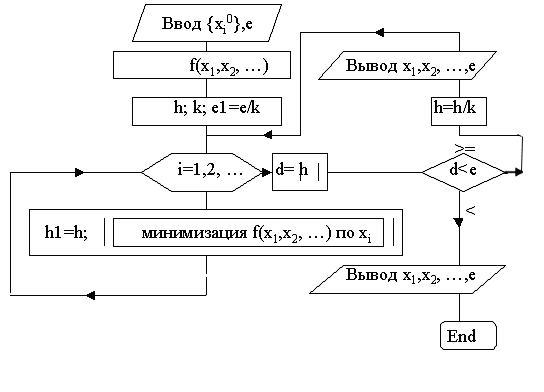
Метод градиентного спуска.
Рассмотрим функцию f, считая для определенности, что она зависит от трех переменных x,y,z. Вычислим ее частные производные дf/дх, дf/ду, дf/дz и образуем с их помощью вектор, который называют градиентом функции:
grad f(x, у, z) = дf (х, у,z) /дх*i+дf( x, у, z)/ду*j+дf(x, y,z)/дг*k.
Здесь i, j, k - единичные векторы, параллельные координатным осям. Частные производные характеризуют изменение функции f по каждой независимой переменной в отдельности. Образованный с их помощью вектор градиента дает общее представление о поведении функции в окрестности точки (х, у,z). Направление этого вектора является направлением наиболее быстрого возрастания функции в данной точке. Противоположное ему направление, которое часто называют антиградиентным, представляет собой направление наиболее быстрого убывания функции. Модуль градиента
______________________
|grad (х, у,z)| =Ö (дf/дх (х, у,z))2 +(дf/ду( x, у, z))2+(дf/дг(x, y,z))2.
определяет скорость возрастания и убывания функции в направлении градиента и антиградиента. Для всех остальных направлений скорость изменения функции в точке (х, у, z) меньше модуля градиента. При переходе от одной точки к другой как направление градиента, так и его модуль, вообще говоря, меняются. Понятие градиента естественным образом переносится на функции любого числа переменных.
Перейдем к описанию метода градиентного спуска. Основная его идея состоит в том, чтобы двигаться к минимуму в направлении наиболее быстрого убывания функции, которое определяется антиградиентом. Эта идея реализуется следующим образом.
Выберем каким-либо способом начальную точку, вычислим в ней градиент рассматриваемой функции и сделаем небольшой шаг в обратном, антиградиентном направлении. В результате мы придем в точку, в которой значение функции будет меньше первоначального. В новой точке повторим процедуру: снова вычислим градиент функции и сделаем шаг в обратном направлении. Продолжая этот процесс, мы будем двигаться в сторону убывания функции. Специальный выбор направления движения на каждом шаге позволяет надеяться на то, что в данном случае приближение к наименьшему значению функции будет более быстрым, чем в методе покоординатного спуска.
Метод градиентного спуска требует вычисления градиента целевой функции на каждом шаге. Если она задана аналитически, то это, как правило, не проблема: для частных производных, определяющих градиент, можно получить явные формулы. В противном случае частные производные в нужных точках приходится вычислять приближенно.
Для оценки частных производных используются разностные методы:
|
![]()
Похожие работы
... Метод преобразования целевой функции, метод штрафных функций, табличный симплекс – метод. Список используемой литературы 1. А.Г.Трифонов. Постановка задачи оптимизации и численные методы ее решения; 2. Б. Банди. Методы оптимизации. Вводный курс., 1988; 3. Мендикенов К.К. Лекции Приложение А using System; using System.Collections.Generic; using System.ComponentModel; using System. ...
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
... Гессе Н. Теорема 3. Пусть Н – симметричная положительно определенная матрица порядка n x n. Рассмотрим задачу минимизации f(x) = cTx + 1 xTHx при условии x О En. Предположим, что задача решена методом Дэвидона - Флетчера - Пауэлла при начальной точке y1 и начальной положительно определенной матрице D1. В частности, пусть lj, j = 1, …, n, – оптимальное решение задачи минимизации f(yj + ldj) при l ...
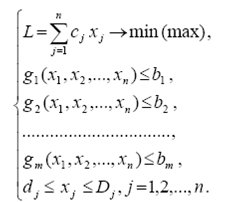


0 комментариев