Совокупность гармонических функций – это совокупность всех решений уравнения Лапласа

2. Совокупность гармонических функций – это совокупность всех решений уравнения Лапласа

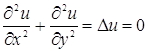, (1)

которое является одним из простейших дифференциальных уравнений с частными производными второго порядка.

Подобно тому, как в случае обыкновенных дифференциальных уравнений для выделения одного определенного решения задают дополнительные условия, так и для полного определения решения уравнения Лапласа требуются дополнительные условия. Для уравнения Лапласа они формулируются в виде так называемых краевых условий, т.е. заданных соотношений, которым должно удовлетворять искомое решение на границе области.

Простейшее из таких условий сводится к заданию значений искомой гармонической функции в каждой точке границы области. Таким образом, мы приходим к первой краевой задаче или задаче Дирихле:

Найти гармоническую в области D и непрерывную в  функцию u(z), которая на границе D принимает заданные непрерывные значения u().

К задаче Дирихле приводится еще, кроме вышеперечисленных, отыскание температуры теплового поля или потенциала электростатического поля в некоторой области при заданной температуре или потенциале на границе области. К ней сводятся и краевые задачи других типов.

б) Обобщенная задача Дирихле.

В приложениях условие непрерывности граничных значений , является слишком стеснительным и приходится рассматривать обобщенную задачу Дирихле [1]:

На границе  области D задана функция , непрерывная всюду, кроме конечного числа точек , где она имеет точки разрыва первого рода. Найти гармоническую и ограниченную в области D функцию u(z), принимающую значения u(z) =  во всех точках непрерывности этой функции.

Если заданная функция  непрерывна, то обобщенная задача Дирихле совпадет с обычной, ибо условие ограниченности функции u(z) следует из условия ее непрерывности в .

Теорема единственности решения обобщенной задачи Дирихле:

В данной области при заданной граничной функции  существует не более одного решения обобщенной задачи Дирихле.

Решение обобщенной задачи Дирихле можно свести к решению обычной задачи Дирихле.

Можно доказать, что:

1.                      для любой односвязной области D и любой кусочно-непрерывной с точками разрыва первого рода граничной функции  решение обобщенной задачи Дирихле существует.

2.                      решение обобщенной задачи Дирихле для единичного круга дается интегралом Пуассона

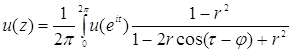 , , ) (2)

3.                      для произвольной области D, мы получим искомую формулу для решения обобщенной задачи Дирихле интегральной формулой Дж.Грина [12, 18]:

 , (3)

где  - производная в направлении внутренней нормали к С,

 ds - элемент длины , соответствующей ,

- элемент внутренней нормали к , - фиксированная произвольная точка области D, а функция ; , реализующая отображение D на единичный круг  и 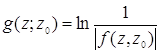 - функция Грина для области D, гармоническую всюду в D кроме точки , где имеет плюс.

Формула Грина (3) выражает решение задачи Дирихле для некоторой области D через логарифм конформного отображения D на единичный круг, т.е. сводит решение задачи Дирихле к задаче конформного отображения. И обратное верно.

Итак, задача конформного отображения области на единичный круг и задача Дирихле для той же области эквивалентны, они сводятся друг к другу с помощью простых операций дифференцирования и интегрирования.

в) Видоизмененная задача Дирихле.

Пусть S⁺ - связная область, ограниченная простыми замкнутыми непересекающимися гладкими контурами , из которых первый охватывает все остальные. Под L мы будем подразумевать совокупность этих контуров , (). Через  - мы обозначим совокупность конечных областей  заключенных, соответственно, внутри контуров  и бесконечной области , состоящей из точек расположенных вне . На контуры  мы наложим еще следующее условие: угол, составляемый касательной к  с постоянным направлением, удовлетворяет условию H; иными словами, мы будем считать, что L удовлетворяет условию Ляпунова [17,24].

Функция  удовлетворяет условию H на этом множестве, если для любых двух  переменной  на этом множестве

 , (4)

где A и  - положительные постоянные показатели Гельдера, А – коэффициент, а  - показатель условия Н и при =1 – условие Липшица, функции, удовлетворяющие условию Н называются непрерывными по Гельдеру и сильнее, чем обычное определение непрерывности.

г) Классическая задача Дирихле для многосвязных областей [24].

Найти (действительную) функцию u(x,y), гармоническую в , по граничному условию

u=f(t) на L, (5)

где f(t) – заданная на L (действительная) непрерывная функция; в случае бесконечной области от функции u(x,y) требуется еще, чтобы она оставалась ограниченной на бесконечности, т.е. и стремится к вполне определенному пределу, когда z уходит в бесконечность.

Напомним, что всякая функция u(z) гармоническая вне круга  в ряд.

, )

абсолютно и равномерно сходящийся вне круга любого радиуса  поэтому u→ при r→.

Для некоторых применений не меньший интерес представляет и следующая задача, которая называется "видоизмененной задачей Дирихле". Термин этот введен в статье Н.И.Мусхелишвили и Д.З.Авазошвили [17].

Видоизмененная задача Дирихле – задача Дирихле

для многосвязных областей.

Найти функцию u(x,y), гармоническую в S⁺, непрерывную в , по следующим условиям:

1. u(x,y)=Ф(z) является действительной частью функции Ф(z), голоморфной в S⁺;