Министерство общего и
профессионального образования РФ
Брянский Государственный
Технический Университет
кафедра
«Высшая математика»
Расчетно-графическая работа №1
Вариант №103
Студент группы 97ДПМ-1
Копачев Д.В.
Преподаватель
Салихов В.Х.
Брянск 1997
1. Описание изделия
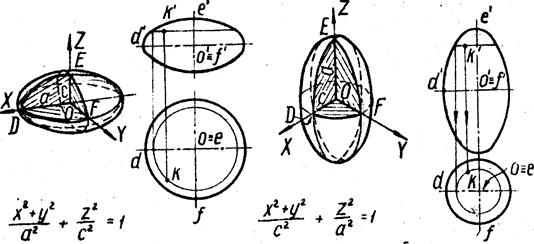
На рисунке 1 изображено в трех проекциях изделие - поверхность, состоящая из одного куска цилиндрической и двух кусков конической поверхностей (КоКоЦ).
Дополнительные сведения:
раствор конуса b = 300
радиус цилиндра R = 5 см
расстояние от оси конуса до оси цилиндра l =2 см
расстояние между осью цилиндра и вершиной каждого из конусов L = 6 см
Выбор системы координат
В качестве начала координат возьмем точку пересечения осей конусов. Ось абсцисс пустим вдоль оси первого конуса, ось ординат - вдоль оси второго конуса, ось аппликат - параллельно оси цилиндра, причем так, чтобы система координат была правой.
Расстояние d от вершин конусов до начала координат находим с помощью Теоремы Пифагора:2
![]() +
l
=
+
l
= ![]() +
2
=
7.7
(см)
+
2
=
7.7
(см)
таким образом ось цилиндра описывается следующим уравнением:
![]()
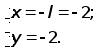
Вершина первого конуса имеет следующие координаты - (-7.7; 0; 0), вершина второго конуса - (0; -7.7; 0).
Аналитическое описание несущих поверхностей
Уравнение цилиндрической поверхности:
(х+2)2+(y+2)2 = R2 ( I )
Параметризация цилиндрической поверхности:
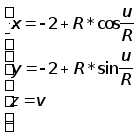 (II)
(II)
Определение положения шва на цилиндрической детали:
потребуем,
чтобы параметр
uО![]()
![]()
![]()
![]() .
При этих значениях
u
шов наиболее
удален от конусов
и описывается
двойным уравнением
x = y =
- l -
.
При этих значениях
u
шов наиболее
удален от конусов
и описывается
двойным уравнением
x = y =
- l -![]() .
.
Уравнение первой конической поверхности:
(x + 7.7)2 tg2b = y 2+ z2 (III)
Параметризация первой конической поверхности:
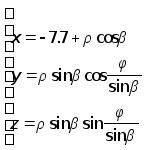 (IV)
(IV)
Определение положения шва на первой конической детали:
потребуем, чтобы jО[-psinb;psinb]
Тогда шов будет наиболее удален от второго конуса.
Уравнение второй конической поверхности:
(y+7.7)2 tg2b=x2+z2 (V)
Параметризация второй конической поверхности аналогично первой (IV):
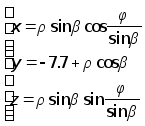 (VI)
(VI)
(Также можно обойтись и без нее за счет использования симметрии).
Описание линии пересечения цилиндра и первого конуса на выкройке цилиндра
Подставим параметризацию цилиндра (II) в уравнение первого конуса (III), получаем уравнение:
(-2+Rcos![]() +7.7)2tg2b=(-2+Rsin
+7.7)2tg2b=(-2+Rsin![]() )2+v2,
которое
в дальнейшем
преобразуется
к виду:
)2+v2,
которое
в дальнейшем
преобразуется
к виду:
v
= v(u) = ±![]() (VII)
(VII)
Знак «+» соответствует «верхней» половине линий отреза, Z і 0 , знак «-» - «нижней» половине этой линии. При некоторых значениях параметра u подкоренное выражение отрицательно, что соответствует отсутствию пересечения образующей цилиндра с первым конусом.
Описание линии пересечения цилиндра и второго конуса на выкройке цилиндра
Линию
пересечения
цилиндра с
первым конусом
следует строить
только при u![]() .
Отражая эту
линию симметрично
относительно
прямой u
=
.
Отражая эту
линию симметрично
относительно
прямой u
= ![]() ,
получаем линию
пересечения
цилиндра со
вторым конусом.
,
получаем линию
пересечения
цилиндра со
вторым конусом.
Описание линии пересечения цилиндра и первого конуса на выкройке конуса
Подставляя параметризацию первого конуса (IV) в уравнение цилиндра (I), получаем уравнение:
(-7.7+rcosb+2)2+
(rsinbcos![]() +2)2
= R2
+2)2
= R2
преобразуем:
(rcosb-5.7)2+
(rsinbcos![]() +2)2
= R2
+2)2
= R2
r2cos2b-2*5.7*rcosb+32.49+r2sin2bcos2![]() +4rsinbcos
+4rsinbcos![]() +4-R2
=
0
+4-R2
=
0
r2(cos2b+sin2bcos2![]() )+2r(-5.7cosb+2
sinbcos
)+2r(-5.7cosb+2
sinbcos![]() )+36.49-R2
= 0
)+36.49-R2
= 0
Отсюда
r=r(j)=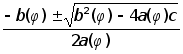 (IX)
(IX)
a(j)=1-
sin2bsin2![]() ;
;
b(j)=2(2sinbcos![]() -5.7cosb);
-5.7cosb);
c=36.49-R2 .
Линия пересечения симметрична относительно луча j=0; ветвь, соответствующая знаку «-» в формуле (IX), посторонняя.
Описание линии пересечения конусов на выкройке первого конуса
Подставляя параметризацию первого конуса (IX), в уравнение второго конуса(V), получаем уравнение:
(rsinbcos![]() +7.7)2tg2b=(-7.7+rcosb)2+r2sin2bsin2
+7.7)2tg2b=(-7.7+rcosb)2+r2sin2bsin2![]() квадратное
уравнение
относительно
переменной
r.
квадратное
уравнение
относительно
переменной
r.
После упрощения получим:
r2(sin2bcos2![]() tg2b-
cos2b-sin2bsin2
tg2b-
cos2b-sin2bsin2![]() )+r(2d(sinbcos
)+r(2d(sinbcos![]() tg2b+cosb))+d2
(tg2b-1)=0
tg2b+cosb))+d2
(tg2b-1)=0
r=![]() , (X)
, (X)
где а =
sin2bcos2![]() tg2b-
cos2b-
sin2bsin2
tg2b-
cos2b-
sin2bsin2![]() ;
;
b
= d(sinbcos![]() tg2b+cosb);
tg2b+cosb);
c = d2(tg2b-1).
Выкройка второго конуса
Она идентична выкройке первого конуса.
Расчет выкройки цилиндрической детали
Подставляем в формулу (VII) конкретные числовые данные и рассчитываем несколько точек (u, v). Результаты отчета заносим в таблицу 1.
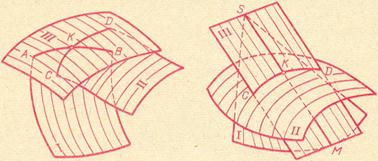
Строим
выкройку
цилиндрической
детали, учитывая,
что линию пересечения
цилиндра с
первым конусом
следует строить
симметрично
относительно
прямой uЈ![]() ;
отражая
эту линию пересечения
относительно
прямой u=
;
отражая
эту линию пересечения
относительно
прямой u=![]() ,
получаем
линию пересечения
цилиндра со
вторым конусом.
Полувысоту
цилиндра примем
равной 8 см.
,
получаем
линию пересечения
цилиндра со
вторым конусом.
Полувысоту
цилиндра примем
равной 8 см.
Расчет выкройки конических деталей
Произведем расчет по формулам (j; r) по формулам (IX, X). Результаты расчетов заносим в таблицы 2 и 3.
Возьмем
сектор ![]() радиуса r0=26см.,
и, учитывая
симметричность
относительно
луча j=0,
построим выкройку
конической
детали.
радиуса r0=26см.,
и, учитывая
симметричность
относительно
луча j=0,
построим выкройку
конической
детали.
Изготовление выкроек деталей, сборка изделия
Изготовим выкройки деталей с припусками на соединение их в изделие, учитывая предыдущее описание. Вырежем и ск
Похожие работы
... поверхности, которые в пересечении с данными поверхностями дают простые для построения линии (например, прямые или окружности). В общем случае вспомогательные секущие плоскости применяют и для построения линии пересечения кривой поверхности гранной. Изложенный общий способ построения линии пересечения одной поверхности другою не исключает применения другого способа, если хотя бы одна из этих ...
... цилиндра, которые соединяем плавной линией. 3. Построение изометрии взаимного пересечения поверхностей фигур Изометрическая проекция – аксонометрическая проекция, при которой длины единичных отрезков на всех трех осях одинаковы По изображениям на комплексном чертеже легко реконструировать объект, решать позиционные и метрические задачи. Для усиления наглядности изображения применяют также ...
... . Прямая линия на чертеже может быть задана проекциями двух ее точек или парой своих проекций. 2.4 Какое положение может занимать прямая относительно плоскостей проекций? машиностроительный чертеж техническая форма Прямая, не параллельная и не перпендикулярная ни к одной из плоскостей проекций, называется прямой общего положения. Прямые, параллельные какой-либо плоскости проекций, называются ...
... » , 1984 г. Æ В.О.Гордон, М.А.Семенцев-Огневский « Курс начертательной геометрии » - Москва, «Наука» , 1977 г. Æ Н.С.Дружинин, Н.Т.Чувиков « Черчение » - Москва, «Высшая школа»,1982г. Æ « Инженерная и компьютерная графика » - под редакцией Э.Т.Романычевой – Москва, «Высшая школа», 1996 г. Æ Э.Д.Мерзон, И.Э.Мерзон « Задачник по машиностроительному черчению » Москва, «Высшая
0 комментариев