Навигация
Вычисление площадей и объёмов с помощью двойных интегралов
22378
знаков
0
таблиц
20
изображений
4. Вычисление площадей и объёмов с помощью двойных интегралов.
а) Объём.
Как мы знаем, объем V тела, ограниченного поверхностью 
, где 
- неотрицательная функция, плоскостью 
и цилиндрической поверхностью, направляющей для которой служит граница области D, а образующие параллельны оси Oz, равен двойному интегралу от функции 
по области D :
Пример 1. Вычислить объем тела, ограниченного поверхностями x=0, у=0, х+у+z=1, z=0 (рис. 17).
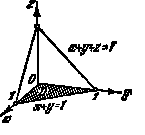
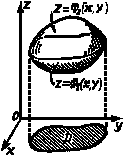
Рис.17 Рис.18
Решение. 
D - заштрихованная на рис. 17 треугольная область в плоскости Оху, ограниченная прямыми x=0, у=0, x+y=1. Расставляя пределы в двойном интеграле, вычислим объем: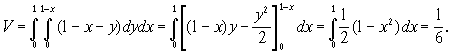 
Итак, 
куб. единиц.
Замечание 1. Если тело, объем которого ищется, ограничено сверху поверхностью 
а снизу—поверхностью 
, причем проекцией обеих поверхностей на плоскость Оху является область D, то объем V этого тела равен разности объемов двух “цилиндрических” тел; первое из этих цилиндрических тел имеет нижним основанием область D, а верхним - поверхность 
второе тело имеет нижним основанием также область D, а верхним - поверхность 
(рис.18).
Поэтому объём V равен разности двух двойных интегралов :
или
(1)
Легко, далее, доказать, что формула (1) верна не только в том случае, когда 
и 
неотрицательны, но и тогда, когда и - любые непрерывные функции, удовлетворяющие соотношению
Замечание 2. Если в области D функция 
меняет знак, то разбиваем область на две части: 1) область D1 где 
2) область D2 ,где 
. Предположим, что области D1 и D2 таковы, что двойные интегралы по этим областям существуют. Тогда интеграл по области D1 будет положителен и будет равен объему тела, лежащего выше плоскости Оху. Интеграл по D2 будет отрицателен и по абсолютной величине равен объему тела, лежащего ниже плоскости Оху, Следовательно, интеграл по D будет выражать разность соответствующих объемов.
б) Вычисление площади плоской области.
Если мы составим интегральную сумму для функции 
по области D, то эта сумма будет равна площади S,
при любом способе разбиения. Переходя к пределу в правой части равенства, получим
Если область D правильная , то площадь выразится двукратным интегралом
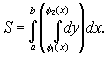
Похожие работы
... формулы Ньютона — Лейбница. Тем самым окончательно оформился общий метод. Предстояло еще научиться находить первообразные многих функций, дать логические основы нового исчисления и т. п. Но главное уже было сделано: дифференциальное и интегральное исчисление создано. Символ ∫ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова summa). Само слово ...
... выражения типа дивергенции по п- мерной области и интеграл по ограничивающей ее сверхповерхности S с уравнением L(x,y,z,…)=0. Если придерживаться прежних обозначений, то формула имеет вид (3) Впрочем, Остроградский не применял геометрических образов и терминов, которыми пользуемся мы: геометрия многомерных пространств в то время еще не существовала. В “Мемуаре об исчислении вариаций кратных ...
... Спорщики возьмут в руки перья и, сказав: “Начнем вычислять” - примутся за расчеты. Как уже отмечалось, Лейбниц одновременно с Ньютоном и независимо от него открыл основные принципы дифференциального и интегрального исчислений. Теория приобрела силу после того, как Лейбницем и Ньютоном было доказано, что дифференцирование и интегрирование - взаимно обратные операции. Об этом свойстве хороню знал и ...
... все содержание посылок, поскольку оно необходимо для вывода, имеет нечувственный характер. (аксиомы, постулаты). VI. Интуитивизм, индивидуалистический эмпиризм и априоризм критической философии в их отношении к теории элементарных методов знания. Три ответа на вопрос о происхождении общих суждений: 1) Путем прямых методов (прямой индукции) = интуитивизм. 2) Общих суждений нет Только иллюзия. ( ...
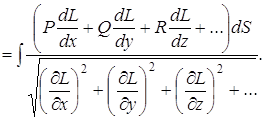
0 комментариев