МОСКОВСКАЯ АКАДЕМИЯ ЭКОНОМИКИ И ПРАВА
РЯЗАНСКИЙ ФИЛИАЛ
КОНТРОЛЬНАЯ РАБОТА
По курсу: «ПРИКЛАДНАЯ МАТЕМАТИКА»
Выполнил: ст-т гр. ЭБ - 241
Лебедев Н. В.
Проверил: профессор
Г. И. Королев
Рязань 2003 г.
Задание 1. Решите, используя формулу полной вероятности, формулу гипотез и формулу Бернулли.
1. Число грузовых автомобилей, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу проезжающих легковых автомобилей как 3:2. Вероятность того, что будет заправляться грузовой автомобиль, равна 0.1. Для легковой автомашины эта вероятность равна 0.2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это легковой автомобиль.
Решение.
Определим событие, вероятность которого надо посчитать. А - к бензоколонке подъехал автомобиль.
Тогда гипотезы:
Н1- к бензоколонке подъехала грузовая машина.
Н2 - к бензоколонке подъехал легковой автомобиль
Р(Н1) = 3/(2+3) = 0.6;
Р(Н2) = 2/(2+3) = 0.4
По условию
Р(А/Н1)=0.1
Р(А/Н2)=0.2
Тогда вероятность события А вычисляется по формуле:
P(A)=Р(A|Н1)*Р(Н1)+Р(A|Н2)*Р(Н2)= 0.6 ![]() 0.1 + 0.4
0.1 + 0.4
![]() 0.2 = 0.06 + 0.08 = 0.14
0.2 = 0.06 + 0.08 = 0.14
P(H2|A)=[ Р(A|Н2)*Р(Н2) ]/P(A) = 0.2 ![]() 0.4/ 0.14 ~ 0.57
0.4/ 0.14 ~ 0.57
2. Вероятность своевременной оплаты счетов шестью потребителями равна 0.8. Найти вероятность того, что к установленному сроку счета не оплатят не более трех потребителей.
Решение.
«Оплатят не более трех потребителей», это значит, что возможны следующие варианты событий:
счета оплатят 0 – потребителей,
1 - потребитель,
2 - потребителя,
3 – потребителя.
По формуле Бернулли найдем вероятность каждого из этих событий.
P_n(k) = C_n(k) ![]() pk
pk![]() (1-p)(n-k), где C_n(k) =
(1-p)(n-k), где C_n(k) = ![]()
n = 6, p = 0.8
1. C_6(0) = ![]() =
= ![]() = 1
= 1
P_6(0) = C_6(0) ![]() 0.80
0.80![]() (1-0.8)(6-0) = 1
(1-0.8)(6-0) = 1 ![]() 1
1![]() 0.26 = 0.000064
0.26 = 0.000064
2. C_6(1) = ![]() =
= ![]() = 6
= 6
P_6(1) = C_6(1) ![]() 0.81
0.81![]() (1-0.8)(6-1) = 6
(1-0.8)(6-1) = 6 ![]() 0.8
0.8 ![]() 0.25 = 0.001536
0.25 = 0.001536
3. C_6(2) = ![]() =
= ![]() =
= ![]() = 15
= 15
P_6(2) = C_6(2) ![]() 0.82
0.82![]() (1-0.8)(6-2) = 15
(1-0.8)(6-2) = 15 ![]() 0.64
0.64 ![]() 0.24 = 0.01536
0.24 = 0.01536
4. C_6(3) = ![]() =
= ![]() =
= ![]() = 20
= 20
P_6(3) = C_6(3) ![]() 0.83
0.83![]() (1-0.8)(6-3) = 20
(1-0.8)(6-3) = 20 ![]() 0.512
0.512 ![]() 0.23 = 0.08192
0.23 = 0.08192
P = P_6(0) + P_6(1) + P_6(2) + P_6(3) = 0.000064 + 0.001536 + 0.01536 + 0.08192 = = 0. 09888 ![]() 0.099 - вероятность того, что к установленному сроку счета не оплатят не более трех потребителей.
0.099 - вероятность того, что к установленному сроку счета не оплатят не более трех потребителей.
Задание 2. Найти среднее квадратическое отклонение вариационного ряда.
X1 800 1000 1200 1400 1600 1800 2000
![]()
n1 1 8 23 39 21 6 2
Среднее квадратическое отклонение случайной величины X вычисляется по формуле Fx = ![]() , где
, где ![]()
![]() – дисперсия случайной величины X.
– дисперсия случайной величины X.
![]() =
= 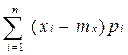
![]() - математическое ожидание случайной величины X.
- математическое ожидание случайной величины X.
![]() 800
800 ![]() 1 + 1000
1 + 1000 ![]() 8 + 1200
8 + 1200 ![]() 23 + 1400
23 + 1400 ![]() 39 + 1600
39 + 1600 ![]() 21 + 1800
21 + 1800 ![]() 6 + 2000
6 + 2000 ![]()
![]() 2 = 139400
2 = 139400
![]() = (800 - 139400)
= (800 - 139400) ![]() 1 + (1000 - 139400)
1 + (1000 - 139400) ![]() 8 + (1200 - 139400)
8 + (1200 - 139400) ![]() 23 + (1400 - -139400)
23 + (1400 - -139400) ![]() 39 + (1600 - 139400)
39 + (1600 - 139400) ![]() 21 + (1800 - 139400)
21 + (1800 - 139400) ![]() 6 + (2000 - 139400)
6 + (2000 - 139400) ![]() 2 =
2 =
= 19209960000 + 153236480000 + 439282520000 + 742716000000 + 398765640000 + + 113602560000 + 37757520000 = 1904570680000
Fx = ![]()
![]() 1380062
1380062
Задание 3. Решить задачу линейного программирования симплексным методом.
Для производства двух видов изделий используются три вида сырья, запасы которого ограничены. Величины запасов приведены в матрице С. Нормы расхода сырья каждого вида на каждое из двух изделий приведены в матрице А , где строки соответствуют виду сырья, а столбцы – виду изделия. Прибыль от реализации изделий указана в матрице P.
Составить план производства изделий так, чтобы предприятие получило максимальную прибыль от их реализации.

 5 9 7710
5 9 7710
А = 9 7 C = 8910 P = ( 10 22 )
3 10 7800
Найдем производственную программу, максимизирующую прибыль L=10х1+22х2.
Затраты ресурсов 1-го вида на производственную программу 5х1+9х2≤7710.
Затраты ресурсов 2-го вида на производственную программу 9х1+7х2 ≤8910.
Затраты ресурсов 3-го вида на производственную программу 3х1+10х2 ≤7800.
Имеем
![]() 5х1+9х2 ≤ 7710
5х1+9х2 ≤ 7710
9х1+7х2 ≤ 8910
3х1+10х2 ≤ 7800
где по смыслу задачи х1≥0, х2≥0.
![]() Получена задача на нахождение условного экстремума. Для ее решения систему неравенств при помощи дополнительных неизвестных х3, х4, х5 заменим системой линейных алгебраических уравнений
Получена задача на нахождение условного экстремума. Для ее решения систему неравенств при помощи дополнительных неизвестных х3, х4, х5 заменим системой линейных алгебраических уравнений
5х1+9х2+х3 = 7710
9х1+7х2+х4 = 8910
3х1+10х2+х5= 7800
где дополнительные переменные имеют смысл остатков соответствующих ресурсов, а именно
х3 – остаток сырья 1-го вида,
х4 – остаток сырья 2-го вида,
х5 – остаток сырья 3-го вида.
Среди всех решений системы уравнений, удовлетворяющих условию неотрицательности
х1≥0, х2≥0, х3≥0, х4≥0, х5≥0, надо найти то решение, при котором функция L=10х1+22х2 будет иметь наибольшее значение.
Ранг матрицы системы уравнений равен 3.
 5 9 1 0 0
5 9 1 0 0
А = 9 7 0 1 0
3 10 0 0 1
![]() Следовательно, три переменные (базисные) можно выразить через две (свободные), т. е.
Следовательно, три переменные (базисные) можно выразить через две (свободные), т. е.
х3 = 7710 - 5х1 - 9х2
х4 = 8910 - 9х1- 7х2
х5= 7800 - 3х1 - 10х2
Функция L = 10х1+22х2 или L - 10х1 - 22х2 = 0 уже выражена через эти же свободные переменные. Получаем следующую таблицу.
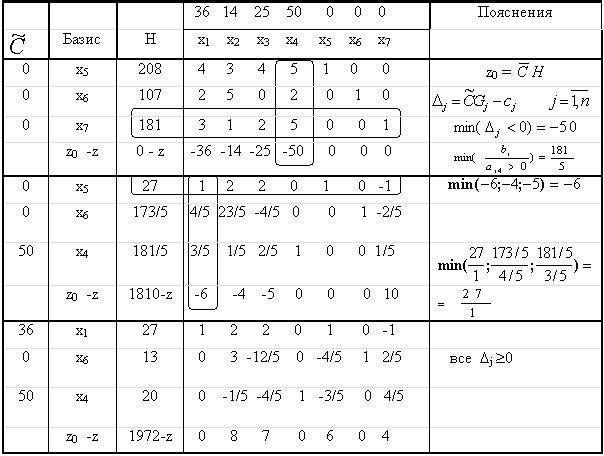
Таблица 1.
| Базисные переменные | Свободные члены | х1 | х2 | х3 | х4 | х5 | |
| х3 | 7710 | 5 | 9 | 1 | 0 | 0 | |
| х4 | 8910 | 9 | 7 | 0 | 1 | 0 | |
| х5 | 7800 | 3 | 10 | 0 | 0 | 1 | |
| L | 0 | -10 | -22 | 0 | 0 | 0 |
Находим в индексной строке отрицательные оценки. Выбираем разрешающий элемент.
В результате получаем следующую таблицу.
Таблица 2.
| Базисные переменные | Свободные члены | х1 | х2 | х3 | х4 | х5 | |
| х3 | 7710 |
| 9 | 1 | 0 | 0 | |
| х4 |
990 | 1 | 7/9 | 0 | 1/9 | 0 | |
| х5 | 7800 | 3 | 10 | 0 | 0 | 1 | |
| L | 0 | -10 | -22 | 0 | 0 | 0 |
Таблица 3.
| Базисные переменные | Свободные члены | х1 | х2 | х3 | х4 | х5 | |
| х3 |
2760 | 0 |
46/9 | 1 | -5/9 | 0 | |
| х1 | 990 | 1 | 7/9 | 0 | 1/9 | 0 | |
| х5 | 4830 | 0 | 69/9 | 0 | -1/3 | 1 | |
| L | 9900 | 0 | -128/9 | 0 | 10/9 | 0 |
Таблица 4.
| Базисные переменные | Свободные члены | х1 | х2 | х3 | х4 | х5 | |
| х2 | 540 | 0 | 1 | 9/46 |
-5/46 | 0 | |
| х1 | 570 | 1 | 0 | -7/46 | 9/46 | 0 | |
| х5 |
690 | 0 | 0 | -3/2 | 1/2 | 1 | |
| L | 17580 | 0 | 0 | 128/46 | -10/23 | 0 |
Таблица 5.
| Базисные переменные | Свободные члены | х1 | х2 | х3 | х4 | х5 | |
| х2 | 690 | 0 | 1 | -3/23 | 0 | 10/46 | |
| х1 | 300 | 1 | 0 | 10/23 | 0 | -81/46 | |
| х4 | 1380 | 0 | 0 | -3 | 1 | 2 | |
| L | 18780 | 0 | 0 | 34/23 | 0 | 20/23 |
Поскольку в индексной строке нет отрицательных оценок, то это значит, что мы получили оптимальную производственная программу:
х1 = 300, х2 = 690, х3 = 0, х4 = 1380, х5 = 0
Остатки ресурсов:
Первого вида – х3=0;
Второго вида – х4=1380;
Третьего вида – х5=0
Максимальная прибыль Lmax=18780.
Похожие работы
... пособие по прикладной химии «Задачи по теоретическим основам химической технологии», составленное по материалам представленной работы. 3. Методика решения задач по теоретическим основам химической технологии Одна из главных задач химической науки и промышленности - получение необходимых человеку веществ (продуктов, материалов). Поэтому большинство учебных химических задач снизано с ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
... . Кроме прочего, подобный факультатив может, по-видимому, частично решить две другие очевидные проблемы военного образования: - во-первых, он в состоянии взять на себя функции задачно-методического "мостика" между математикой и специальными дисциплинами (в инженерных вузах подобный мостик достаточно эффективно реализуется общепрофессиональными дисциплинами); - во-вторых - это потенциально главная ...
... какая-либо из имеющихся. ж) Придумайте взвешивающую формулу (ее придется объяснить при защите курсовой работы!) и найдите по ней худшую и лучшую операции. Произвести математико-статистический анализ за T лет Xt, Kt, Lt (t = 1, …, T) о выпуске продукции (в стоимостном виде), ОПФ и числе занятых исследуемого производственного экономического объекта:а) найти прогноз выпуска, фондов и занятых ...







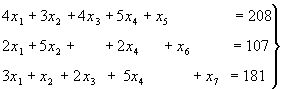
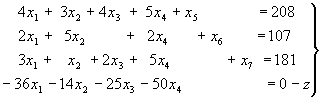
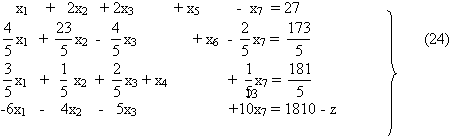
0 комментариев