Пусть имеется n+1 переменная x1, x2, ..., xn, y, которые связаны между собой так, что каждому набору числовых значений переменных x1, x2, ..., xnсоответствует единственное значение переменной y. Тогда говорят, что задана функция f от n переменных. Число y, поставленное в соответствие набору x1, x2, ..., xn называется значением функции f в точке (x1, x2, ..., xn), что записывается в виде формулы y = f(x1,x2,..., xn) или y =y(x1,x2,..., xn).
Переменные x1, x2, ..., xn являются аргументами этой функции, а переменная y функцией от n переменных.
Далее будем говорить лишь о функции двух переменных. Для функций большего числа переменных все факты, о которых будет идти речь, или аналогичны или сохраняются без всякого изменения. Аргументы функции двух переменных будем обозначать как правило x и y, а значение функции z.
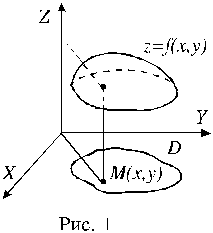
Множество D называется областью определения функции.
Поскольку любую пару чисел x,y можно рассматривать как пару координат точки M на плоскости, вместо z=f(x,y) можно писать z=f(M).При этом аргументами функции будут координаты x,y точки M.
Числа
x,y
можно рассматривать
как координаты
вектора ![]() ,
исходящего
из начала координат
и с концом в
точке M(x,y).
Тогда функция
двух переменных
будет функцией
вектора,
что записывается
в виде формулы
z = f(
,
исходящего
из начала координат
и с концом в
точке M(x,y).
Тогда функция
двух переменных
будет функцией
вектора,
что записывается
в виде формулы
z = f(![]() ),
причем аргументами
функции являются
координаты
вектора
),
причем аргументами
функции являются
координаты
вектора ![]() .
.
График функции двух переменных есть множество точек (x,y,f(x,y)), где (x,y)D. График представляет собой некоторую поверхность. Пример такой
поверхности приводится на рисунке 1.
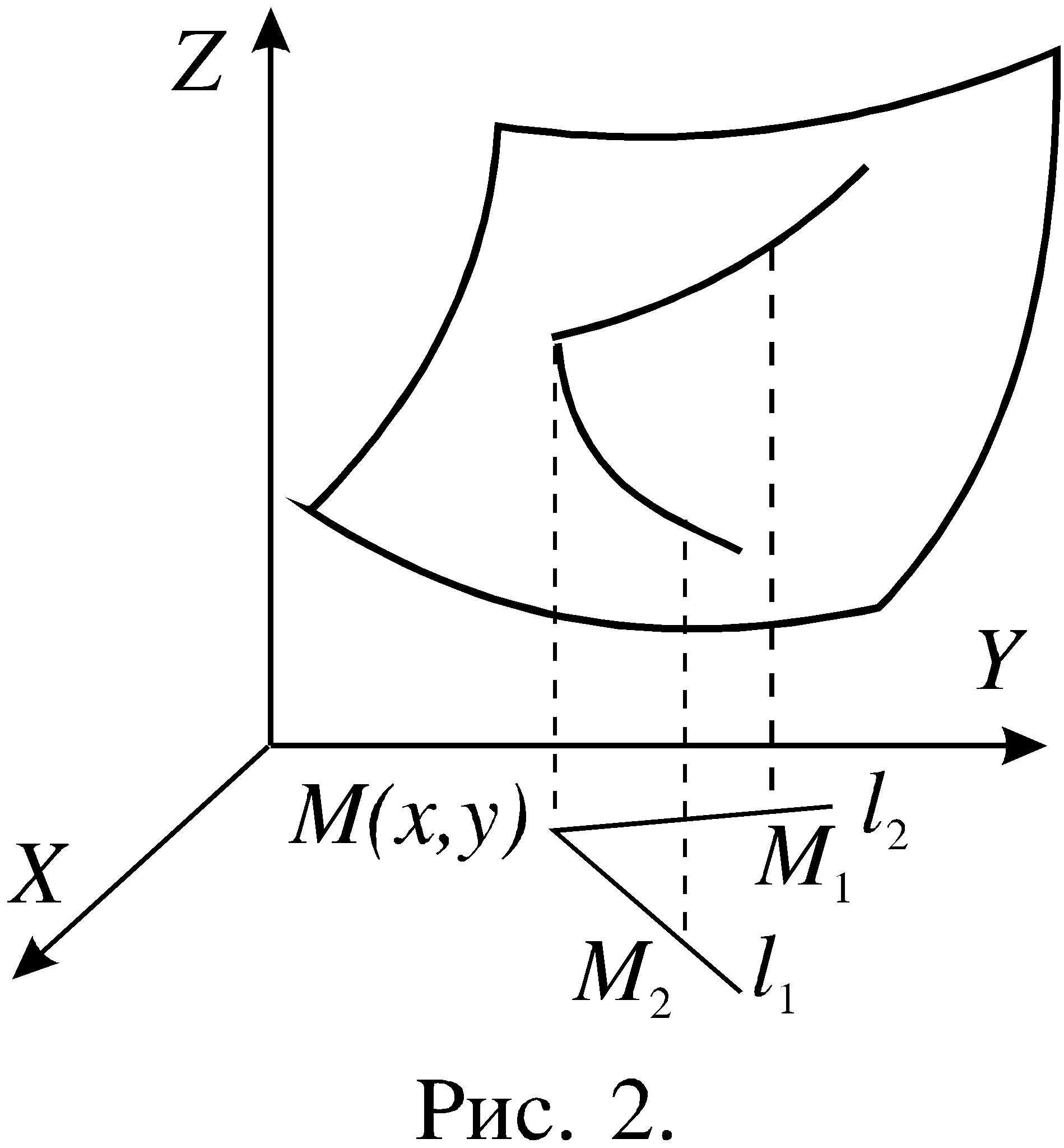
Одним из подходов к исследованию функций двух переменных является изучение поведения функции в точке, то есть определение направлений, в которых функция убывает или возрастает, и определение скорости возрастания или убывания.
Можно использовать другой подход. Пусть имеется функция z = f(x,y) c графиком, представляющим собой некоторую поверхность.
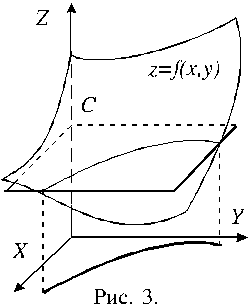
В микроэкономике, в предположении что потребитель приобретает лишь два вида товаров: A и B, вводится понятие общей полезности TU, как функции двух аргументов: Q1 и Q2 – количеств потребленных товаров A и B, соответственно:
TU = TU(Q1,Q2). (1)
Очевидно, что все линии уровня функции TU(Q1,Q2) составляют семейство кривых безразличия (Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 125).
Пусть в плоскости XOY заданы две точки: M0(x0,y0) и M1(x1,y1). Расстояние между этими точками рассчитывается по формуле
![]() . (2)
. (2)
Пусть некоторое положительное число. -окрестностью V точки M0(x0,y0) называется множество всех точек, координаты x,y которых удовлетворяют неравенствам
![]() .
.
Очевидно, что -окрестность точки M0(x0,y0) представляет собой круг радиуса с выколотым центром.
Точка M0(x0,y0) называется точкой минимума функции z = f(x,y), если существует такое положительное число , что из условия M(x,y) V (x0,y0) следует f(x,y) > f(x0,y0).
Точка M0(x0,y0) называется точкой максимума функции z = f(x,y), если существует такое положительное число , что из условия M(x,y) V (x0,y0) следует: f(x,y) 0 найдется такое число > 0, что для всех точек M(x,y) из -окрестности точки M0(x0,y0) выполняется неравенство
|f(x,y) - A| 0 (это точки, лежащие внутри первого и третьего координатных углов), и есть точки, где z(x,y) 0, то минимум, а если A
Похожие работы
... М. В. Неоклассическая модель чистой монополии. М.: ИМЭМО, АН СССР, 1990. 3. Лейбенстайн X. Аллокативная эффективность в сравнении с "Х-эффективностью" // Теория фирмы. С. 477—506. 4. Маленво Э. Лекции... Гл. III. § 9. С. 80—85. 5. Робинсон Дж. Экономическая теория... Гл. 3—5. С. 88—130. 6. Стиглер Дж. Совершенная конкуренция: исторический ракурс // Теория фирмы. С. 299—328. 7. Самуэльсон П. ...
... , и что он может сделать для этого человека. Детоводительство, коим является педагогика, в большей мере, чем любое другое служение, зависит от того, кого мы собрались вести. [3] Значение духовно-нравственного воспитания Духовная жизнь русского человека, тайна его рождения и смерти, взлетов и падений, выбора жизненного пути незримо, но неразрывно соединены с разворачивающейся усилием отнюдь не ...
... преобладает над рациональной), а определение других сторон содержания (тематики и проблематики в первую очередь) факультативным и вспомогательным. 1.2. Принципы школьного анализа лирического произведения Вместе с тем изучение лирических произведений—один из сложнейших вопросов методики. Восприятие лирики дается учащимся труднее, чем усвоение эпоса и драмы, т. к. поэтические образы отличаются ...
... гнезда", "Войны и мира", "Вишневого сада". Важно и то, что главный герой романа как бы открывает целую галерею "лишних людей" в русской литературе: Печорин, Рудин, Обломов. Анализируя роман "Евгений Онегин", Белинский указал, что в начале XIX века образованное дворянство было тем сословием, "в котором почти исключительно выразился прогресс русского общества", и что в "Онегине" Пушкин "решился ...
0 комментариев