Министерство образования Российской Федерации
Башкирский государственный педагогический университет
Кафедра математического анализа Дипломная квалификационная работаАвтор: Гарипов Ильгиз.
Тема: Свойства усредненной функции с сильной осцилляцией.
К защите допущен ____________
Заведующий кафедрой к.ф. м. н. доцент Сафаров Т.Г.
Руководитель д.физ-мат. наук. профессор Султанаев Я.Т.
Уфа 2001
Содержание
Стр.
Введение 3 § 1 Свойства функции§ 2 Свойства функции ![]() и ее производных. 5
и ее производных. 5
2.1 ![]() 5
5
2.2 ![]() 6
6
2.3 ![]() где a>0 7
где a>0 7
2.4 ![]() 9
9
3.1 ![]() 11
11
3.2
![]() 11
11
3.3 ![]() 12
12
3.4 ![]() 13
13
4.1 ![]() 14
14
4.2
![]() 15
15
4.3 ![]() 15
15
4.4 ![]() 16
16
Заключение 17
Литература 18
Введение
Пусть ![]() произвольная функция,
определенная на
произвольная функция,
определенная на ![]() , и
, и ![]() при
при ![]()
Введем в рассмотрение функцию ![]() с помощью следующего равенства:
с помощью следующего равенства:
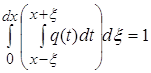 (1)
(1)
Назовем эту функцию усреднением функции ![]()
Это название оправдано так как из (1) и теоремы о среднем для интегралов можем заключить
![]()
![]()
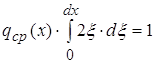
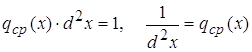
§ 2 Свойства функции
1. Если ![]() , при
, при ![]() , то
, то ![]() при
при ![]()
Доказательство:
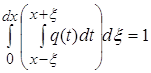 ,
, ![]() ,
, ![]()
![]() " N >0,
" N >0, ![]() :
: ![]()
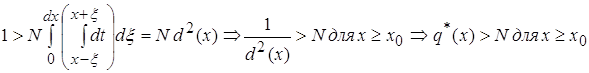
2. 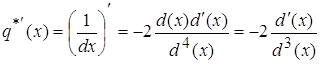 (2)
(2)
3. 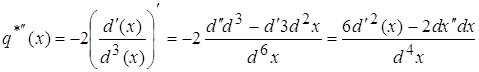 (3)
(3)
Дифференцируя формулу (1) по dx получаем
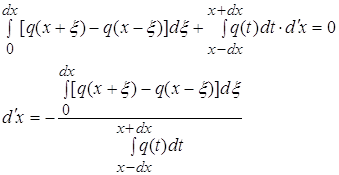 (4)
(4)
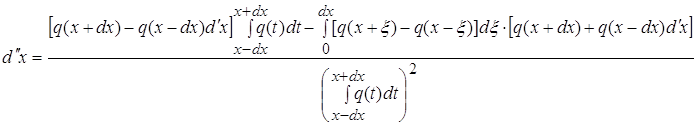 (5)
(5)
§ 2 Свойства функции ![]() и ее производных.
и ее производных.
2.1 ![]()
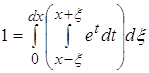
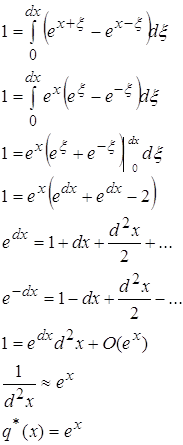
2.2 ![]()
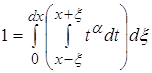
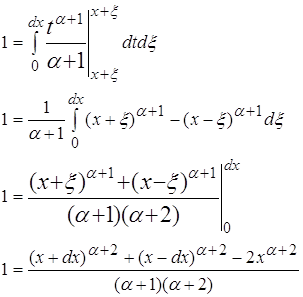
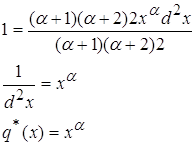
2.3 ![]() где a>0;
где a>0;
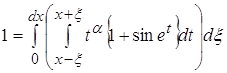
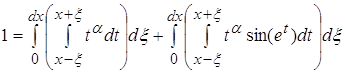
Разделим интеграл на два интеграла и вычислим их отдельно.
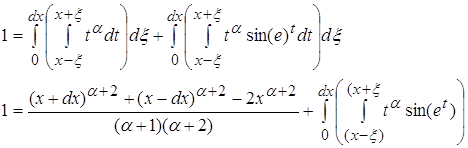
Второй интеграл не оказывает влияния на первый, так как при ![]() функция стремится к 0.
функция стремится к 0.
Доказательство:
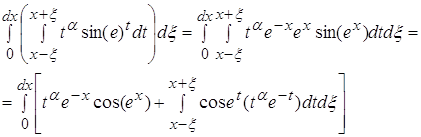
Рассматривая второй интеграл, мы получаем:
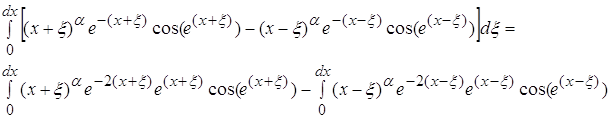
Рассматривая первый интеграл, получаем:
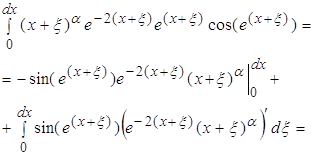
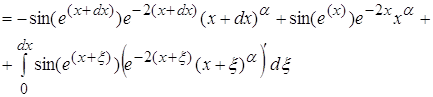
Последние два слагаемых полученных при интегрировании содержат в произведении ![]() , то есть при возрастании x эти слагаемые будут очень быстро уменьшатся и весь интеграл при
, то есть при возрастании x эти слагаемые будут очень быстро уменьшатся и весь интеграл при ![]() становится очень малым по сравнению с первой частью. Поэтому можно считать что при
становится очень малым по сравнению с первой частью. Поэтому можно считать что при ![]()
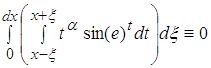
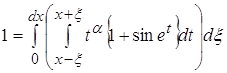
![]()
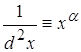
2.4. ![]()
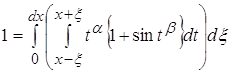
Наложить на![]() ограничение, такое чтобы
ограничение, такое чтобы ![]() присутствие
присутствие ![]() не влияло на поведение функции.
не влияло на поведение функции.
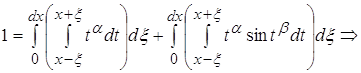
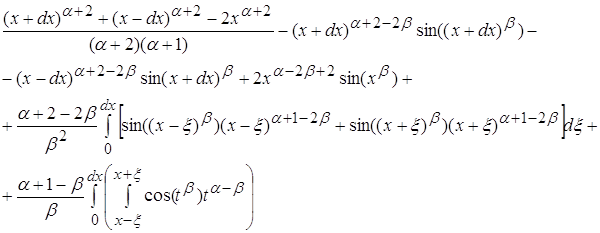
Рассматривая полученное выражение можно заметить что
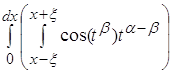
становится пренебрежительно малым по отношению к остальной части
как только ![]() . Ограничение №1
. Ограничение №1
В тоже время
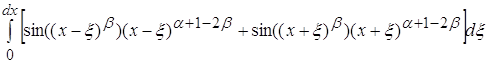
Становится бесконечно малым как только ![]() . Ограничение №2
. Ограничение №2
![]()
должен быть очень малым при ![]() то есть
то есть
![]()
так как ![]() ограниченная функция, к 0 должен стремится
ограниченная функция, к 0 должен стремится ![]() .
.
![]()
![]()
![]()
![]() Ограничение №3
Ограничение №3
![]()
Следовательно, ![]() ограничение на
ограничение на ![]() удовлетворяющее поставленной задаче, при котором присутствие
удовлетворяющее поставленной задаче, при котором присутствие ![]() не влияет на поведение функции
не влияет на поведение функции ![]() .
.
§ 3 Рассмотрим поведение функции ![]() для случаев:
для случаев:
3.1) ![]()
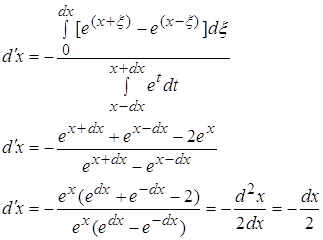
![]()
![]()
3.2) ![]()
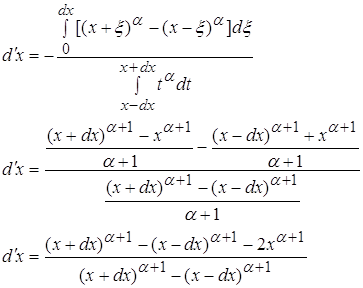
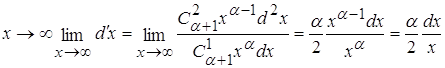
![]()
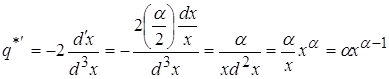
3.3) ![]()
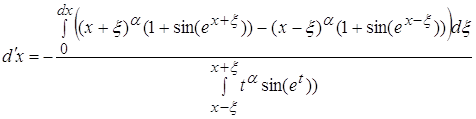
Вычислим отдельно интегральное выражение, стоящее в числителе:
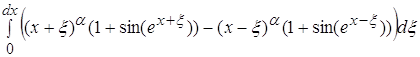 =
=
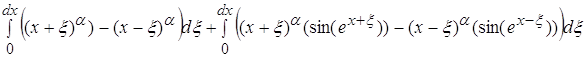 =
=
![]()
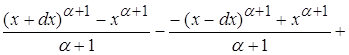
![]()
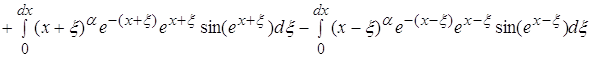
![]()
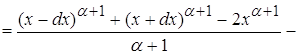
![]()
рассматривая пределы при ![]() видим что на поведение функции оказывает влияние только главный член
видим что на поведение функции оказывает влияние только главный член ![]()
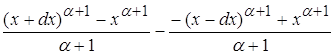
Поведение данной функции при ![]() эквивалентно поведению функции
эквивалентно поведению функции
![]() (*)
(*)
Вычислим интеграл в знаменателе:
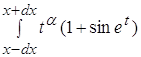 =
=
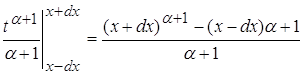
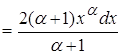
![]() (**)
(**)
Учитывая (*)и (**) получаем
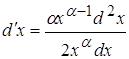
![]()
Следовательно, по формуле (2) получаем ![]()
3.4 ![]()
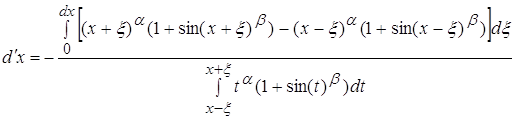
Отдельно вычислим числитель и знаменатель:
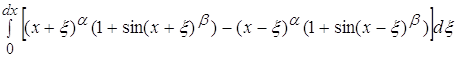
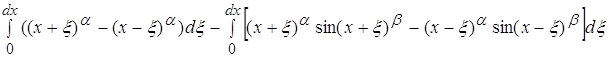
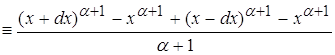
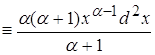
Вычислим знаменатель:
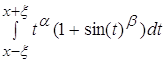
Разделив интеграл на 2 интеграла, мы получаем:
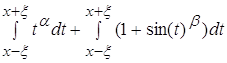
По пункту 2.4 можем вывести что второй интеграл не влияет на поведение функции при ![]()
Следовательно, знаменатель:
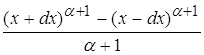
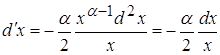
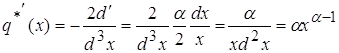
§4. Рассмотрим поведение второй производной ![]()
Для облегчения вычислений введем обозначения:
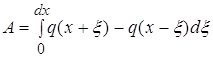
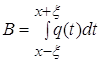
![]()
![]()
При этом формула для ![]() примет вид
примет вид 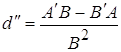 (6)
(6)
4.1 ![]()
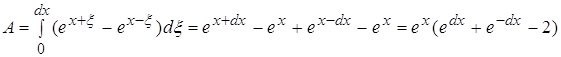
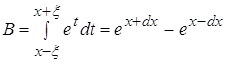
![]()
![]()
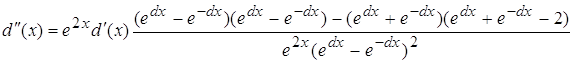
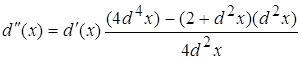
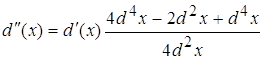
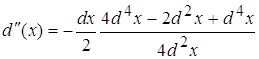
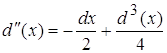
Виду того, что d(x) очень мал то 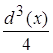 будет несравним с d(x) т.е.
будет несравним с d(x) т.е.
![]()
4.2 ![]()
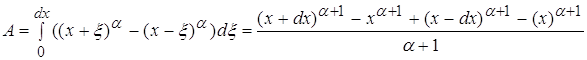
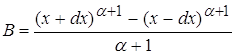
![]()
![]()
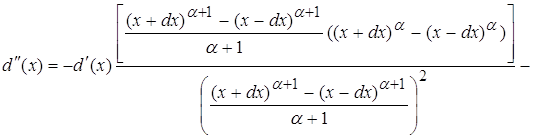
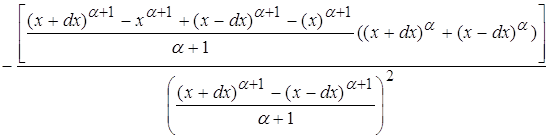
используя равенства, полученные в пункте 2.2 и 3.2, преобразуя данное равенство, приходим к выражению:
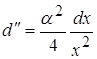
(Все выкладки приводить не буду в виду их громоздкости и сложности для восприятия. Добавлю только что все выкладки, примененные в данном пункте полностью повторяют ограничения и эквивалентные выражения, использованные в пунктах 2.2 и 3.2).
Отсюда следует что ![]()
4.3 ![]()
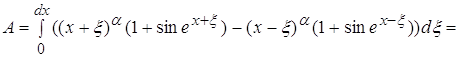
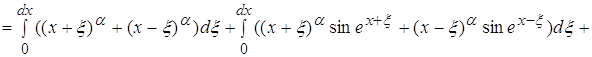
Используя данные, полученные в п.3.3 получаем что
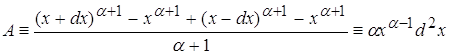
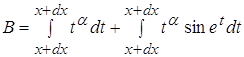
Возвращаясь к п. 3.3 находим:
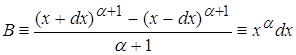
![]()
![]()
Вычисляя ![]() по формуле 6, получаем:
по формуле 6, получаем:
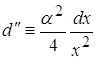
и ![]()
4.4 ![]()
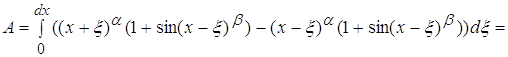
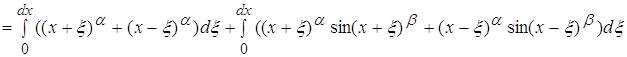
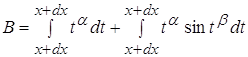
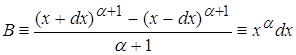
![]()
![]()
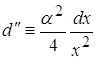
и ![]()
Заключение
В результате проведенного исследования поведения усредненной функции в случае осциллирующих коэфициентов, получены данные приведенные в следующей таблице:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Похожие работы
... мере, синергетическим стилем мышления может быть некой платформой для открытого творческого диалога между учеными, мыслителями, деятелями искусства, имеющими различные творческие установки и взгляды на мир. 2. Некоторые парадоксальные следствия синергетики Множество новых парадоксальных идей, образов и представлений возникает в синергетике. Кроме того, с точки зрения синергетики может быть ...
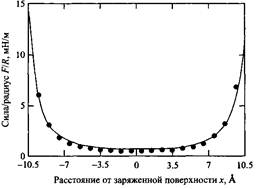
... цепей ПЭО. Накапливаясь в растворе, ПЭО создает осмотическое давление, действующее на молекулы белка. Это очень интересный механизм, в том смысле, что вводимый полимер влияет на взаимодействие между коллоидными частицами, не находясь между ними! Диапазон сил притяжения деплеции по порядку величины совпадает с радиусом инерции полимерной молекулы. Для идеального полимера радиус инерции равен г1/2, ...
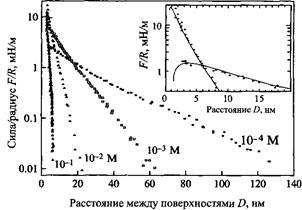
... найдена зависимость U(r) при 0.3мкм<r<1.8мкм. Она достаточно хорошо совпала с известным лондоновским потенциалом U(r)~K0(r/l ), где K0 - функция Макдональда, l - глубина проникновения магнитного поля в сверхпроводник. Наилучшее соответствие достигается при выборе l =(39.1± 0.7)нм, что неплохо согласуется с табличным значением l =(45± 1)нм при T=4.5K. К числу не совсем понятных особенностей ...
... покоя нейтрино, обнаружению осцилляций нейтрино. Если окажется, что масса нейтрино отлична от нуля, то масса вещества во Вселенной должна в основном определяться массой нейтрино. Ядерные реакции Развитие ядерной физики в большой степени определяется исследованиями в такой важной ее области, как ядерные реакции. Однако после того, как Резерфорд впервые наблюдал ядерную реакцию, до появления ...

0 комментариев