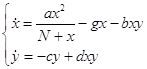
Задание:
1. Ввести новые переменные, максимально уменьшив число параметров системы.
2. Найти неподвижные точки системы и исследовать их характеристики в зависимости от параметров системы.
3. Исследовать поведение предельных циклов. Доказать их существование/несуществование.
4. Построить фазовые портреты системы при всех возможных параметрах системы.
5. Дать биологическую интерпретацию полученным результатам.
1. Вводим новые переменные x à Ax, y à By, t à Tt и переписываем систему:
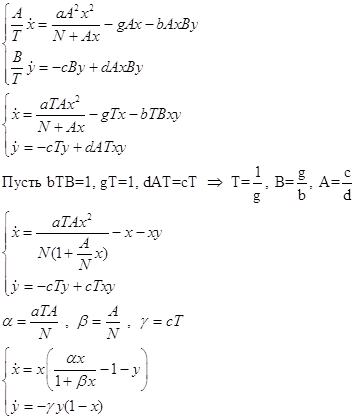
2. Нахождение неподвижных точек преобразованной системы
2.1 x=0,y=0 ==> O(0,0)
2.2 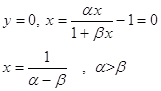
P![]()
2.3 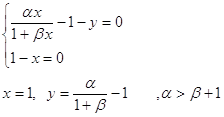
Q![]()
3. Характеристики неподвижных точек
Запишем Якобиан нашей системы
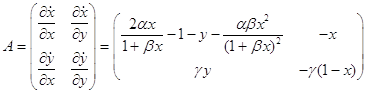
3.1 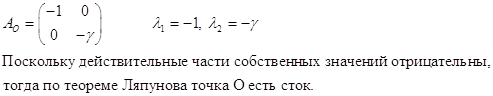
3.2 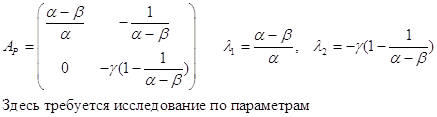
3.3 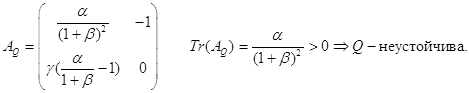
Проведем дополнительное исследование, обозначив на параметрическом портрете возможные области значений ![]() .
.
а) точка О – сток, как было показано выше;
б) точка Р![]() :
:
![]()
Область 1: ![]()
Область 2: ![]()
Точка Р – исток (неуст. узел)
Область 3: ![]()
Точка Р – седло
в) точка Q![]() :
:
Область 1: 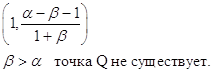
Область 2: ![]()
Область 3: ![]()
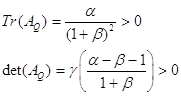
Точка Q – исток ( неустойчивый узел)
Кроме того, при поиске собственных значений Якобиана возникает уравнение
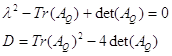
Решение уравнения D<0 производилось графически , поскольку аналитическое решение в этом случае представляется затруднительным. Для этого использовался математический пакет Maple 6. При фиксированном значении ![]() были рассмотрены точки (
были рассмотрены точки (![]() )области 3, для которых проверялось неравенство D<0. Таким образом, как видно из рисунка, в 3-ей области появляется подобласть 3’. Неравенство D<0 выполняется в области 3 – 3’ , где вещественные части собственных значений будут положительны. В этой области точка Q превращается в неустойчивый фокус.
)области 3, для которых проверялось неравенство D<0. Таким образом, как видно из рисунка, в 3-ей области появляется подобласть 3’. Неравенство D<0 выполняется в области 3 – 3’ , где вещественные части собственных значений будут положительны. В этой области точка Q превращается в неустойчивый фокус.
Запишем результаты исследования характеристик точек в таблицу:
| \Область Точка | 1 | 2 | 3 | 3 – 3’ |
| O | сток | сток | сток | сток |
| P | не сущ. | исток | седло | седло |
| Q | не сущ. | не сущ. | исток | неуст. фокус |
4.1 Параметрические области системы
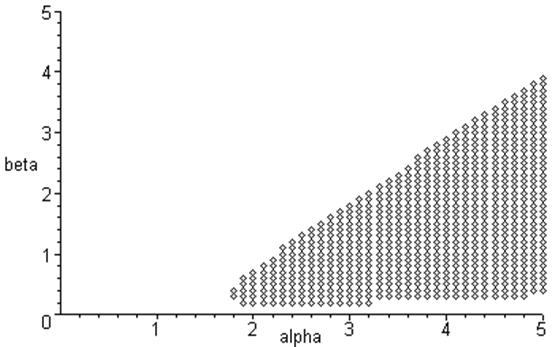
4.2 Область 1: ![]()
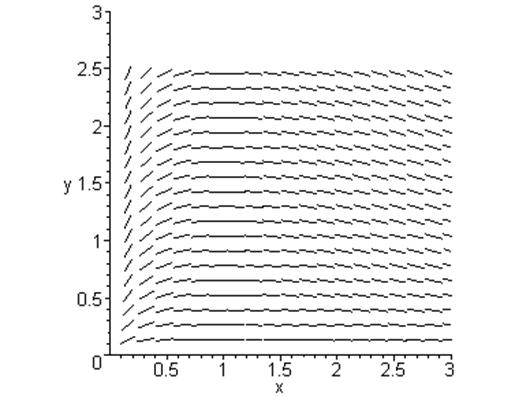
4.3 Область 2: ![]()
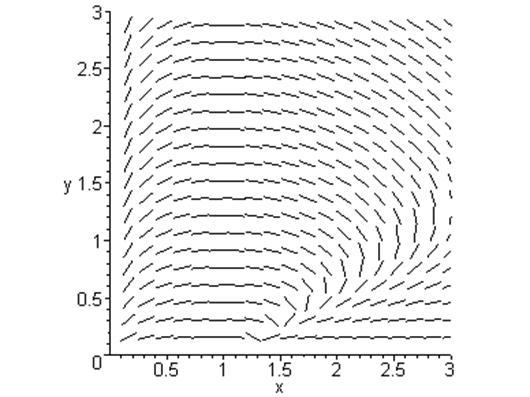
4.3 Область 3’ : ![]()
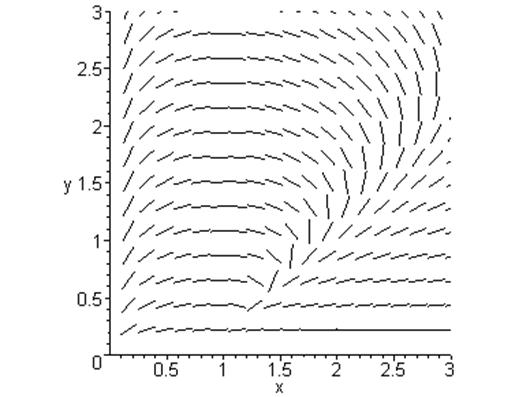
4.5 Область 3 – 3’ : ![]()
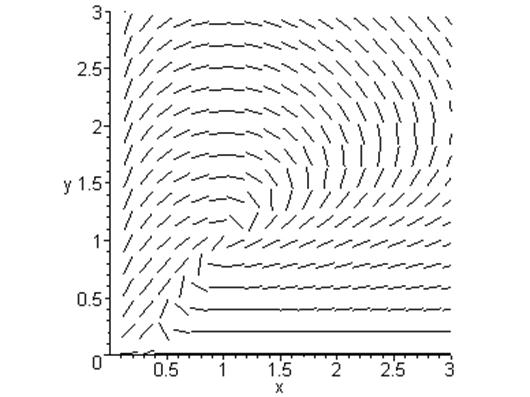
5. Биологическая интерпретация модели.
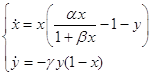
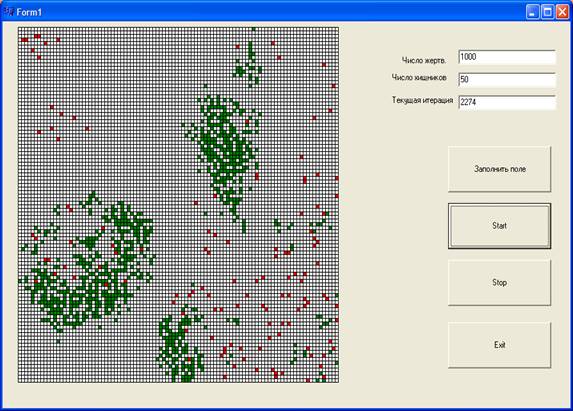
Данная система представляет собой модель взаимного влияния в природе двух животных видов – хищников и жертв. Как видно из рисунков, в этой системе оба вида вымирают. Предельных циклов в системе нет. X – жертвы, Y – хищники. Динамику взаимодействия двух видов описывают три функции: g(x) – функция динамики численности жертв, p(x) – трофическая функция жертв (характеризует число жертв убитых одним хищником), q(x) – трофическая функция хищников (характеризует влияние числа жертв, убиваемых одним хищником, на изменение численности популяции хищников).
![]()
Похожие работы
... В результате открылись колоссальные возможности для изучения различных типов динамики метаболической системы. Регуляторные системы и ритмические явления Однако в настоящее время кажется очевидным, что при рассмотрении резких переключений из одного состояния в другое, которые имеют место в клетках, нужно пользоваться терминами, описывающими эпигенетические регуляторные системы. Здесь имеются ...
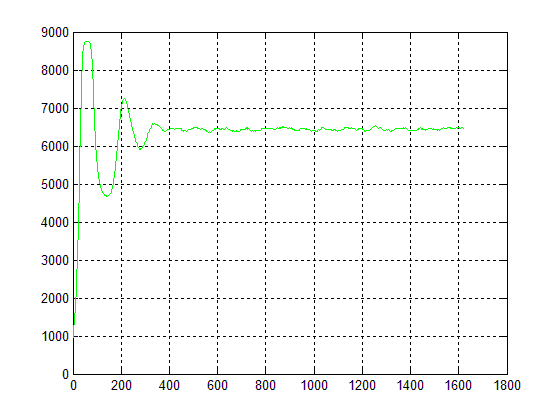
... При запуске с другим набором параметров все хищники в системе погибли и были получены следующие результаты График численности хищников от времени и их полное вымирание График численности хищников и жертв На вымирание хищников, система среагировала резким ростом численности жертв и началом стабилизации к некоторому равновесному значению. 4. Вымирание обоих видов При запуск
... типа MESH. 13.6. Графика пакета plots 13.6.1. Общая характеристика пакета plots Пакет plots содержит почти полсотни графических функции, существенно расширяющих возможности графики системы Maple V. В реализации R4 этот пакет содержит следующие функции: ——————————— animate Создает мультипликацию 2D графиков функций. animated Создает мультипликацию 3D графиков функции. changecoords ...
... . 1.4.3 Метод Рунге-Кутта Этим методам посвящено много работ, и они хорошо изложены в много-численных учебниках (см., например, [2,3]). 2. Модели осциллирующих процессов в живой природе 2.1 Модель Лотки 2.1.1 Осциллирующие химические реакции В некоторых химических реакциях концентрации реагентов осциллируют в следующем смысле. Соединение каких-то начальных веществ приводит к их ...


0 комментариев