Идентификация параметров осциллирующих процессов в живой природе, моделируемых дифференциальными уравнениями

Санкт-Петербургский Государственный Университет

Реферат

Идентификация параметров осциллирующих процессов в живой природе, моделируемых дифференциальными уравнениями

Выполнила студентка 312гр.

Варламова А.А.

Проверил Токин И.Б

Санкт-Петербург

2007

Оглавление

1.    Идентификация параметров в системах описываемых ОДУ

1.1 Градиентные уравнения

1.2 Уравнения в вариациях

1.3 Функционалы метода наименьших квадратов

1.4 Численное решение градиентных уравнений

1.4.1 Полиномиальные системы

1.4.2 Метод рядов Тейлора

1.4.3 Метод Рунге-Кутта

2. Модели осциллирующих процессов в живой природе

2.1 Модель Лотки

2.1.1 Осциллирующие химические реакции

2.1.2 Осцилляция популяций в системе “хищник-жертва”

2.2 Другие модели

3. Идентификация параметров модели Лотки

3.1 Дифференциальные уравнения

3.2 Постановки задачи идентификации и функционалы МНК

3.3 Как ускорить вычисления

3.4 Численный эксперимент

4. О других методах идентификации

Литература

1.         Идентификация параметров в системах, описываемых ОДУ

1.1      Градиентные уравнения

Градиентные уравнения возникают в связи с задачей нахождения экстремумов функций многих аргументов. Важно, что эти аргументы сами могут зависеть от решений каких-то уравнений - численных, дифференциальных и иных. Мы будем использовать их для минимизации функций аргументов, за-висящих от решений обыкновенных дифференциальных уравнений.

Рассмотрим вещественнозначную функцию  аргумента ,  и пусть  и . Тогда величина

 (1)

то есть производная функции  по направлению  характеризует скорость изменения  при изменении  в направлении вектора .

Из формулы (1) получаем:

 (2)

где  - градиент функции , а это дает:

(3)

(4)

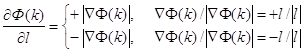 (5)

Таким образом, вектор  является направлением наискорейшего рос-та функции  в точке , а вектор  - это направление наискорейшего ее убывания в этой точке.

Градиентной кривой функции  называют кривую , , касательное направление к которой в каждой точке  противоположно направлению вектора градиента , то есть сов-падает с направлением наискорейшего убывания .

Это означает, что удовлетворяет дифференциальному уравнению:

(6)

или в координатной форме:

 (7)

К уравнениям (6) или (7) добавляем начальные условия:

(8)

или в координатной форме:

 (9)

Решение задачи Коши (6),(8) (или (7),(9)) определяет градиентную кривую проходящую через точку . Будем рассматривать это решение как век-тор-функцию  аргументов  и .

Зададимся теперь целью найти точку  локального минимума неотрицательной функции , если она существует и достаточно близка к . Если за начальное приближение для  взять , то движение вдоль градиентной кривой, проходящей через  (то есть движение вдоль траектории решения ) можно считать идеальным путем к точке .

Если решение задачи (6),(8) существует при , то при любом та-ком  получаем, что:

 при  (11)

 при  (12)

и мы вправе ожидать, что

(13)

Метод градиентных уравнений нахождения локального минимума функции  заключается в численном интегрировании задачи Коши (6),(8) вдоль оси  до достижения точки , достаточно близкой к .

Похожие работы

Устройства генерирования и канализации субмиллиметровых волн

Скачать

117222

0

10

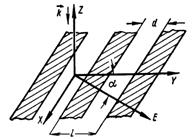
... , то необходимость в дополнительной линии передачи вообще отпадает при передаче энергии на сотни километров, поскольку вся излучаемая энергия может быть перехвачена приемным устройством с апертурой приемлемых размеров. В диапазоне субмиллиметровых волн отношение допустимых размеров апертур к длине волны заметно уменьшается, тем не менее в ряде случаев подобные квазиоптические линии передачи могут ...