Навигация
Разность одинаковых чётных степеней на сумму их оснований делится без остатка
15661
знак
0
таблиц
0
изображений
2. Разность одинаковых чётных степеней на сумму их оснований делится без остатка .
Пусть P(x) = x2k , тогда P(a) = a2k .
Разность одинаковых чётных степеней x2k - a2k равна P(x) – P(a) .
P(a) = a2k = (-a)2k = P(-a) , т.е. x2k - a2k = P(x) – P(-a).
По следствию 5
P(x) - P(-a) = (x –(- a))Q(x)=
= (x + a)Q(x)
а это значит , что
x2k – a2k = (x + a)Q(x) или
(x2k – a2k)/(x + a) = Q(x) ,
т.е. разность одинаковых чётных степеней на сумму их оснований делится без остатка , что и требовалось доказать .
Итак ,
(x2k – a2k)/(x + a) = x2k-1 – ax2k-2 + … +a2k-2x + a2k-1.
3. Разность одинаковых нечётных натуральных степеней на сумму их оснований не делится .
Пусть P(x) = x2k+1 - a2k+1 – разность одинаковых нечётных степеней .
По теореме Безу при делении x2k+1 - a2k+1 на x + a = x – (-a) остаток равен
R = P(-a) = (-a)2k+1 – a2k+1 = -2a2k+1
Т. к. остаток при делении не равен 0 , то разность одинаковых нечётных натуральных степеней на сумму их оснований не делится , что и требовалось доказать .
4. Сумма одинаковых нечётных натуральных степеней на сумму их оснований делится без остатка .
Пусть P(x) = x2л+1 , P(-a) = (-a)2л+1 = -а2л+1 ,
тогда P(x) – P(-a) = x2k+1 + a2k+1 – сумма одинаковых нечётных натуральных степеней .
По следствию 5
P(x) - P(-a) = x2k+1 + a2k+1= (x –(- a))Q(x)=
= (x + a)Q(x),
а это значит , что
(x2k+1 + a2k+1)/(x + a) = Q(x) ,
т.е. сумма одинаковых нечётных натуральных степеней на сумму их оснований делится без остатка , что и требовалось доказать .
Итак ,
(x2k+1 + a2k+1)/(x + a) = x2k - ax2k-1 + … - a2k-1x + a2k.
5. Сумма одинаковых чётных натуральных степеней на сумму их оснований не делится .
Пусть P(x) = x2k + a2k – сумма одинаковых чётных степеней .
По теореме Безу при делении x2k + a2k на x + a = x – (-a) остаток равен
R = P(-a) = (-a)2k + a2k = 2a2k.
Т. к. остаток при делении не равен 0 , то сумма одинаковых чётных натуральных степеней на сумму
их оснований не делится, что и требовалось доказать.
Остановимся на рассмотрении некоторых случаев применения теоремы Безу к решению практических задач .
Пример 1.
Найти остаток от деления многочлена
x3 – 3x2 + 6x – 5
на двучлен x – 2 .
По теореме Безу
R = P3 (2) = 23 – 3*22 + 6*2 – 5 = 3 .
Ответ: R = 3 .
Пример 2.
Найти остаток от деления многочлена
32x4 – 64x3 + 8x2 + 36x + 4
на двучлен 2x – 1 .
Согласно следствию 1 из теоремы Безу
R=P4(1/2)=32*1/24–64*1/23 + 8*1/22+36*1/2+4=
= 2 – 8 + 2 + 18 + 4 =18 .
Ответ: R = 18 .
Пример 3.
При каком значении a многочлен
x4 + ax3 + 3x2 – 4x – 4
делится без остатка на двучлен x – 2 ?
По теореме Безу
R = P4 (2) = 16 + 8a + 12 – 8 – 4 = 8a +16.
Но по условию R = 0 , значит
8a + 16 = 0 ,
отсюда
a = -2 .
Ответ: a = -2 .
Пример 4.
При каких значениях a и b многочлен
ax3 + bx2 – 73x + 102
делится на трёхчлен
x2 – 5x + 6 без остатка ?
Разложим делитель на множители :
x2 – 5x + 6 = (x – 2)(x – 3) .
Поскольку двучлены x – 2 и x – 3 взаимно просты , то данный многочлен делится на x – 2 и на x – 3 , а это значит , что
по теореме Безу
R1 = P3 (2) = 8a + 4b – 146 + 102 =
= 8a + 4b – 44 = 0
R2 = P3 (3) = 27a+9b – 219 + 102 =
= 27a +9b -117 =0
Решим систему уравнений :
8a + 4b – 44 = 0
27a + 9b – 117 = 0
2a + b = 11
3a + b = 13
Отсюда получаем :
a = 2 , b = 7 .
Ответ: a = 2 , b = 7 .
Пример 5.
При каких значениях a и b многочлен
x4 + ax3 – 9x2 + 11x + b
делится без остатка на трёхчлен
x2 – 2x + 1 ?
Представим делитель так :
x2 – 2x + 1 = (x – 1)2
Данный многочлен делится на x – 1 без остатка ,
если по теореме Безу
R1 = P4 (1) = 1 + a – 9 + 11 + b = a + b + 3 = 0.
Найдём частное от деления этого многочлена на x – 1 :
_ x4 + ax3–9x2 + 11x–a –3 x – 1
x4 – x3 x3+(a+1)x2+(a–8)x+(a+3)
_(a + 1)x3 – 9x2
(a + 1)x3 – (a + 1)x2
_(a – 8)x2 + 11x
(a – 8)x2 – (a –8)x
_(a + 3)x – a – 3
(a + 3)x – a – 3
0
Частное
x3+(a+1)x2+(a–8)x+(a+3)
делится на (x – 1) без остатка , откуда
R2 = P3 (1) = 1 + (a + 1)*1 +(a – 8)*1 + a+3 =
=3a – 3 = 0 .
a + b + 3 = 0
3a – 3 = 0
a + b =-3
a = 1
Из системы : a = 1 , b = -4
Ответ: a = 1 , b = -4 .
Пример 6.
Разложить на множители многочлен P(x) = x4 + 4x2 – 5 .
Среди делителей свободного члена число 1 является корнем данного многочлена P(x) , а это значит , что по следствию 2 из теоремы Безу P(x) делится на (x – 1) без остатка :
_x4 + 4x2 – 5 x – 1
x4 – x3 x3 + x2 + 5x + 5
_x3 + 4x2 – 5
x3 – x2
_5x2 – 5
5x2 – 5x
_5x – 5
5x – 5
0
P(x)/(x – 1) = x3 + x2 + 5x + 5 , значит
P(x) = (x – 1)(x3 + x2 + 5x + 5).
Среди делителей свободного члена многочлена x3 + x2 + 5x + 5 x = -1 является его корнем , а это значит , что по следствию 2 из теоремы Безу x3 + x2 + 5x + 5 делится на (x + 1) без остатка :
_x3 + x2 +5x + 5 x + 1
x3 + x2 x2 +5
_5x + 5
5x + 5
0
(x3 + x2 +5x + 5)/(x + 1) = x2 +5 ,
значит
x3 + x2 +5x + 5 = (x +1)(x2 +5).
Отсюда
P(x) = (x – 1)(x +1)(x2 +5) .
По следствию 7 (x2 + 5) на множители не раскладывается , т.к. действительных корней не имеет , поэтому P(x) далее на множители не раскладывается .
Ответ : x4 + 4x2 – 5 = (x – 1)(x +1)(x2 +5) .
Пример 7.
Разложить на множители многочлен P(x) = x4 + 324 .
P(x) корней не имеет , т.к. x4 не может быть равен -324 , значит , по следствию 7 P(x) на множители не раскладывается .
Ответ : многочлен на множители не раскладывается .
Пример 8.
Какую кратность имеет корень 2 для многочлена
P(x) = x5 - 5x4 + 7x3 – 2x2 + 4x – 8 .
Определение: Если многочлен P(x) делится без остатка на (x – a)k , но не делится на (x – a)k+1 , то говорят , что число a является корнем кратности k для P(x).
_x5 - 5x4 + 7x3 – 2x2 + 4x – 8 x – 2
x5 - 2x4
x4 – 3x3 + x2 + 4
_-3x4 + 7x3 – 2x2 + 4x – 8
-3x4 + 6x3
_x3 – 2x2 + 4x – 8
x3 – 2x2
_4x – 8
4x – 8
0
_x4 – 3x3 + x2 + 4 x – 2
x4 – 2x3 x3 – x2 – x – 2
_-x3 + x2 + 4
-x3 +2x2
_-x2 + 4
-x2 + 2x
_-2x + 4
-2x + 4
0
_ x3 – x2 – x – 2 x – 2
x3 – 2x2 x2 + x + 1
_x2 – x – 2
x2 – 2x
_x – 2
x – 2
0
x2 + x + 1 на x – 2 не делится , т.к. R=22 + 2 + 1=
=7.
Значит , P(x)/(x – 2)3 = x2 + x + 1 , т.е. корень 2 имеет кратность 3 для многочлена P(x) .
Ответ: корень 2 имеет кратность 3 для многочлена P(x) .
Пример 9.
Составить кубический многочлен , имеющий корень 4 кратности 2 и корень -2 .
По следствию 3 , если многочлен P(x) имеет корень 4 кратности 2 и корень –2 , то он делится без остатка на (x – 4)2(x + 2) , значит
P(x)/(x – 4)2(x + 2) = Q(x) ,
т.е. P(x) = (x – 4)2(x + 2)Q(x) =
= (x2 – 8x +16)(x + 2)Q(x) =
= (x3 – 8x2 + 16x +2x2 – 16x + 32)Q(x) =
= (x3 – 6x2 + 32)Q(x).
(x3 – 6x2 + 32) - кубический многочлен , но по условию P(x) – также кубический многочлен, следовательно , Q(x) – некоторое действительное число .
Пусть Q(x) = 1 , тогда P(x) = x3 – 6x2 + 32 .
Ответ: x3 – 6x2 + 32 .
Пример 10.
Определите a и b так , чтобы -2 было корнем многочлена P(x) = x5 + ax2 + bx + 1, имеющим по крайней мере кратность два .
Если -2 – корень многочлена P(x) кратности два , то по следствию 3 P(x) делится на (x + 2)2 без остатка (R = 0)
(x + 2)2 = x2 + 4x + 4
_x5 + ax2 + bx + 1 x2 + 4x + 4
x5 + 4x4 + 4x3 x3 – 4x2 + 12x – (a + 32)
_-4x4–4x3–ax2+bx+1
-4x4 – 16x3 – 16x2
_12x3 + (16 – a)x2 + bx + 1
12x3 +48x2 + 48x
_-(a + 32)x2 + (b – 48)x + 1
-(a + 32)x2 – 4(a + 32)x – 4(a + 32)
(4a +b – 48 + 128)x + 4a + 129
R = (4a +b – 48 + 128)x + 4a + 129 =
= (4a +b + 80)x + 4a + 129
Но R = 0 , значит
(4a +b + 80)x + 4a + 129 = 0 при любых x .
Это возможно при условии , что
4a +b + 80 = 0 ,
4a + 129 = 0
Решим систему двух уравнений :
4a +b + 80 = 0 a = -32,25
4a + 129 = 0 b = 49
Ответ: a = -32,25 , b = 49 .
Из рассмотренных примеров видно , что теорема Безу находит применение при решении задач , связанных с делимостью многочленов (нахождение остатка при делении многочленов , определение кратности многочленов и т.д. ) , с разложением многочленов на множители , с определением кратности корней и многих других .
Теорема Безу находит применение при рассмотрении одной из важнейших задач математики – решении уравнений .
Литература. 1. Бородин А.И., Бугай А.С.Биографический словарь деятелей в области математики.
2. Математическая энциклопедия.
3. Яремчук Ф.П., Рудченко П.А.
Алгебра и элементарные функции.
4. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварц- бурд С.И.
Алгебра и математический анализ.
5. Курош А.Г.
Курс высшей алгебры.
Похожие работы
... (x-a) равен f(a), а по условию a является корнем f(x), а это значит, что f(a)=0, что и требовалось доказать. Из данного следствия теоремы Безу видно, что задача решения уравнения f(x)=0 равносильна задаче выделения делителей многочлена f, имеющих первую степень (линейных делителей). Следствие 3: Если многочлен f(x) имеет попарно различные корни a1, a2 ,… ,an ,то он делится на произведение ...
... которого на один ниже степени многочлена Также данный метод называют понижением степени. Благодаря данному способу можно найти оставшиеся корни многочлена. 2.4. Примеры использования теоремы. Пример. Найти остаток от деления многочлена на . Решение. На основании теоремы Безу подставляем вместо x число -5. Получаем r(x)= В результате мы получили остаток r(x) равный 180. Пример. С ...
... тьюринговых машин. Проблема заключается в следующем как по любому заданному шрифту установить к какому классу относится машина, зашифрованная им: к классу самоприменимых или несамоприменимых. Теорема 2. Проблема распознавания самоприменимости алгоритмически неразрешима. 3). Проблема эквивалентности слов для ассоциативных исчислений. Рассмотрим некоторый алфавит и множество слов в этом алфавите. ...
... f(x) непрерывна в замкнутом круге Е, то она ограничена. Лемма №6. Действительная функция комплексного переменного f(x) непрерывная в замкнутом круге Е достигает своего минимума и максимума. Доказательство основной теоремы. Лемма №1.Надо доказать, что |f(x0+x)-f(x0)|<e. Докажем Лемму №1 сначала для многочлена без свободного члена и при x0=0 ЕслиA=max(|a0 |,|a1|,…,|a n-1|) и (1) то ...
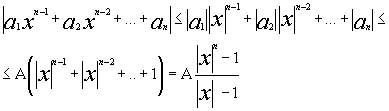
0 комментариев