Одно дифференциальное уравнение с несколькими неизвестными. «…те, в которых имеются флюксии больше чем двух величин»

3.   Одно дифференциальное уравнение с несколькими неизвестными. «…те, в которых имеются флюксии больше чем двух величин»

Ньютон рассматривает и решение каждого из случаев.

Решение первого случая.

«Прими единственную имеющуюся в уравнению флюэнту за соотнесенную величину и, преобразовав уравнение в соответствии с этим допущением (т. е. установив отношение флюксии второй величины к флюксии первой и значение этого отношения, выраженного через простые члены(Т. е. разложенного в степенной ряд)), помножь значение отношения флюксий на соотнесенную величину. Затем раздели каждый член этого выражения на показатель степени, в которую возведена в нем соотнесенная величина; то что ты таким образом получишь, и будет равно другой текущей величине.»

В современных терминах это выглядит так: нужно уравнение f(x, y) = 0 привести к виду y’= j (x) и проинтегрировать. Процедура же интегрирования сводится к разложению j в степенной ряд и последующему почленному интегрированию ряда.

Решение второго случая.

«До сих пор речь шла об уравнениях, которые заключают одну флюэнту. Когда же в уравнении появляются обе, то уравнение прежде всего следует привести к уже указанному виду, полагая с одной стороны отношение флюксий, а с другой  равную ему сумму простых членов.

Кроме того, если какой-либо член преобразованного таким образом уравнения представляет дробь с флюэнтой в знаменателе, то он должен быть освобожден от подобного знаменателя при помощи вышеприведенной замены текущей величины.

Таким образом, если дано уравнение

или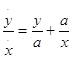

то в силу наличия члена ^a/_x я беру произвольное b и вместо x пишу b + x или b - x или x- b. Если написать b + x, то получается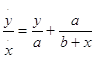

Обращая затем при помощи деления член a/(b + x) в бесконечный ряд, я вывел бы, что 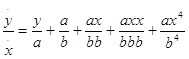 и т.д.

Правило: Подготовив таким образом (если это нужно) уравнение, расположи члены по степеням флюэнт, сперва ставя те, которые не содержат отнесенной величины, затем те, которые содержат ее в наименьшей степени, и т. д. Таким же образом распредели по отдельным родам члены согласно степеням соотнесенной величины и члены, которые образуют первый род (именно, которые не содержат отнесенной величины), запиши в виде горизонтального ряда слева направо, а остальные выпиши в левом столбце так, чтобы они образовывали нисходящий ряд, как это показано в нижеприведенной таблице.

Приготовив таким образом ряды, помножь первый или низший член первого рода на соотнесенную величину и раздели произведение на показатель его степени и то, что при этом получится, введи в результат (Предлагается проинтегрировать ряд по степеням независимой переменной).Затем подставь это значение вместо отнесенной величины в те члены уравнения, которые расположены в левом столбце; второй член результата ты получишь из следующего низшего члена по тому же способу, каким добыт первый член результата. Повторяя эти действия, ты можешь продолжить результат сколь угодно»

По существу, здесь предлагается конечный алгоритм следующих действий:

1.   В уравнение подставляется разложение решения в ряд по степеням независимого аргумента с неопределенными коэффициентами.

2.   Коэффициенты при одинаковых степенях приравниваются.

3.   Получившаяся (бесконечная) система алгебраических уравнений получается треугольной, поэтому можно выписать ее решение в явном виде).

Это станет еще ясней из рассмотрения нескольких примеров.

Пример 3.

Пусть дано уравнение

= 1  3x + y + xx + y.

Члены его 1  3x + xx, не содержащие отнесенной величины y, расположены, как видишь, в первой строке, а остальные члены y и xy  в левом столбце.

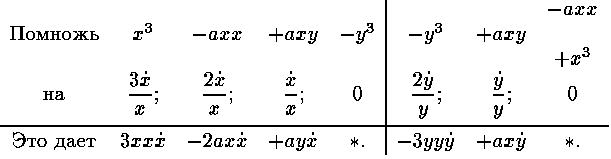
Пример 4.

Точно так же, если требуется определить соотношение между x и y из уравнения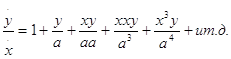

в котором ряд предполагается продолжающимся до бесконечности, то наверху я пишу 1, остальные члены выписываю в левом столбце и затем произвожу действие, как это видно из представленной таблицы.

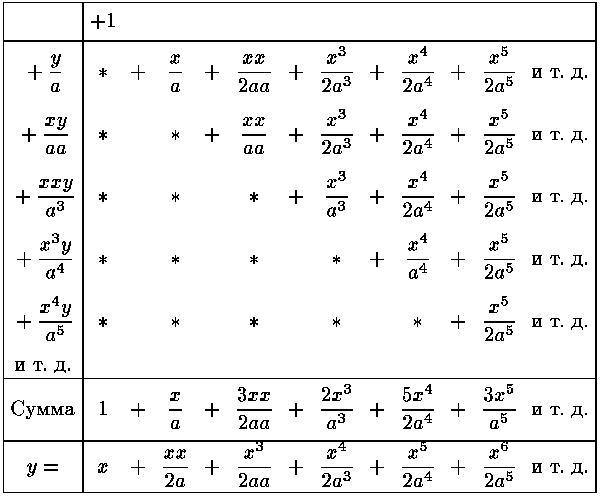
Предполагая, что мне предложено было найти выражение для y лишь до шестой степени x, я в силу этого опускаю при действии все члены, которые, как я предвижу, не будут использованы; это отмечается знаком "и т. д.", который я ставлю вместо отсеченных частей рядов»

Приведенные выше сведения были частично взяты из перевода работы "Метод флюксий и бесконечных рядов с приложением его к геометрии кривых", которая была написана Ньютоном в 1664-71 гг. и издана уже после его смерти.

Метод флюксий применяется здесь к большому числу геометрических вопросов (задачи на касательные, кривизну, экстремумы, квадратуры, спрямления и др.); здесь же выражается в элементарных функциях ряд интегралов от функций, содержащих квадратный корень из квадратичного трёхчлена. Большое внимание уделено в "Методе флюксий" интегрированию обыкновенных дифференциальных уравнений, причём основную роль играет представление решения в виде бесконечного степенного ряда.

Во введении к "Рассуждению о квадратуре кривых" (основной текст 1665-66, введение и окончательный вариант 1670, опубликован 1704) и в "Началах" он намечает программу построения метода флюксий на основе учения о пределе, о "последних отношениях исчезающих величин" или "первых отношениях зарождающихся величин", не давая, впрочем, формального определения предела и рассматривая его как первоначальное.

В сочинении "Анализ при помощи уравнений с бесконечным числом членов" (1669, опубликовано 1711) Ньютон вычислил производную и интеграл любой степенной функции. Различные рациональные, дробно-рациональные, иррациональные и некоторые трансцендентные функции (логарифмическую, показательную, синус, косинус, арксинус) Ньютон выражал с помощью бесконечных степенных рядов.

  Заключение

Таким образом, разработанная сначала Ньютоном, затем Лейбницем теория флюксий дала начало дифференциальному и интегральному исчислениям в том виде, в котором мы их знаем сегодня.

  Литература:

1.   Вавилов С. И., Исаак Ньютон, М., 1961;

2.   Философия и история математики. Колмогоров А. Н., Математика, в книге: Большая Советская энциклопедия, 2 изд., т. 26, М., 1954;

3.   Математика, её содержание, методы и значение, т. 1-3, М., 1956;

4.   Юшкевич А. П., История математики в средние века, М., 1961;

5.   Степанов В. В., Курс дифференциальных уравнений, 8 изд., М., 1959;

6.   Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 2 изд., М., 1965;

7.   Исаак Ньютон. Математические работы, ОНТИ, М.-Л., 1937