Навигация
Уравнения математической физики
Определение.
Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции. Если неизвестная функция зависит от одной переменной, то это обыкновенное дифференциальное уравнение, иначе - уравнение в частных производных.
Определение.
Наивысший порядок производных неизвестной функции, входящих в уравнение, называется порядком уравнения.
Определение.
Дифференциальное уравнение называется линейным, если производные и сама неизвестная функция входят в уравнение линейным образом.
µ§ (1)
Пусть выбран любо鵧, где µ§, и его норма:
µ§- дифференциальный оператор.
µ§ - запись линейного диф. уравнения с помощью диф. оператора. (2)
Определение.
Открытое, связное множество µ§ называется областью.
По умолчанию будем считать область ограниченной.
Через µ§или µ§ будем обозначать границу области.
Определение.
µ§ - (n-1)-мерное многообразие S в µ§ принадлежит классу µ§ (µ§), если
для µ§ и µ§ такие, что:
µ§, где µ§
µ§ однозначно проектируется на плоскость µ§, при этом:
D - проекция данного множества на плоскость µ§, µ§ - k раз непрерывно дифференцируема в D по всем переменным.
Можно разбить поверхность на части, в каждой части можно одну координату выразить через другие непрерывно дифференцируемой функцией.
µ§ - множество k раз непрерывно дифференцируемых функций в Q.
µ§ - множество k раз непрерывно дифференцируемых функций в µ§.
µ§, аналогично µ§.
µ§ - множество финитных k раз непрерывно дифференцируемых функций.
Аналогично: µ§.
§ 2. Классификация линейных уравнений в частных производных второго порядка.
µ§.
µ§ - матрица квадратичной формы.
µ§ - n вещественных собственных значений матрицы A
µ§ - количество положительных собственных значений.
µ§ - количество отрицательных собственных значений.
µ§ - количество нулевых собственных значений с учетом кратности.
1.Если µ§= n или µ§= n, то это эллиптическое уравнение.
Ex: Уравнение Пуассона
µ§.
2.Если µ§ = n - 1, µ§ = 1, или µ§ = 1, µ§ = n - 1, то уравнение гиперболическое.
Ex: µ§ - волновое уравнение.
Для уравнения Лапласа:
µ§
Для волнового уравнения:
µ§
3.Если µ§, а µ§, то ультрагиперболическое уравнение.
Ex: µ§.
4.Если µ§, то параболическое уравнение.
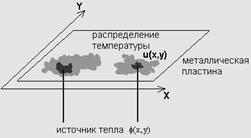
Ex: µ§, и - уравнение теплопроводности.
µ§
Определение.
Каноническим видом линейного дифференциального уравнения в частных производных называется такой вид, когда матрица A является диагональной.
Приведение к каноническому виду.
1) y=y(x), то:
µ§
Уравнение (1) в новой системе координат:
µ§ (1')
Матрица Якоби:
µ§.
В результате:
µ§ |
Ex:
µ§
гиперболическое уравнение.
µ§ - канонический вид волнового уравнения.
Замечание: тип уравнения может быть различный в различных точках.
§ 3.Постановка начальных и краевых задач для уравнений в частных производных.
Задача Коши для волнового уравнения:
µ§ µ§
Уравнение теплопроводности
µ§ µ§
Уравнение Пуассона
µ§
Определение.
Если малые изменения правой части уравнения приводят к большим изменениям в решении, то задача считается некорректной.
µ§ (6)
µ§ (7.1)
µ§ (7.2)
µ§ (7.3)
(6)(7.1) - первая краевая задача, задача Дирихле.
(6)(7.2) - вторая краевая задача, задача Неймана.
(6)(7.3) - третья краевая задача.
Волновое уравнение.
µ§ (8)
µ§ (9)
µ§ (10)
µ§ (11.1)
µ§ (11.2)
µ§ (11.3)
(8) (9) (10) (11.1) - смешанные
(11.2) задачи
(11.3) (краевые задачи)
µ§ - единичный вектор внешней нормали к поверхности.
На µ§ задаются начальные условия.
На боковой поверхности - краевые задачи.
Параболическое уравнение.
µ§ (12)
µ§ (13)
µ§ (14.1)
µ§ (14.2)
µ§ (14.3)
(12) (13) (14.1) - первая, вторая и третья смешанные задачи
(14.2) для уравнения
(14.3) теплопроводности.
(14.1) - на границе задана температура;
(14.2) - задан тепловой поток;
(14.3) - задан теплообмен с окружающей средой.
§ 4. Решение смешанных задач для волнового уравнения методом Фурье (разделением переменных).
Первая смешанная задача.
µ§ (1)
µ§ (2)
µ§ (3)
µ§ (4)
µ§ (5)
µ§ (6)
Собственные значения (5) - (6) вещественны, имеют конечную кратность.
µ§
µ§ - изолир. µ§.
µ§ - ортонормированный базис в µ§.
В симметричной матрице собственные вектора, соответствующие разным собственным значениям, попарно ортогональны.
Пусть функции µ§ - разложены по базису µ§
µ§
тогда и u(t,x) можно разложить по базису µ§ : µ§
Почленно дифференцируем ряд 2 раза:
µ§
µ§ (7)
Путём разложения решения в ряды по собственным функциям задачи алгебраизуем задачу, получаем счётное число обыкновенных дифференциальных уравнений.
µ§ (8)
µ§ (9)
(7) (8) (9) - задача.
Решим однородное уравнение для (7):
µ§
- общее решение однородного уравнения (7)
µ§
µ§ (10)
µ§
В результате: µ§ - частное решение неоднородного уравнения (7).
µ§ - общее решение уравнения (7).
Подставим (8) и (9) в решение:
µ§
т.е. µ§.
| µ§ |
Замечание: не обоснована сходимость рядов.
§ 5.Решение смешанных задач уравнения теплопроводности методом Фурье (разделения переменных).
µ§ (1)
µ§ (2)
µ§ (3)
µ§ (4)
µ§ (5)
µ§ - собственные векторы и собственные значения.
µ§
µ§ (6)
µ§
µ§ - общее решение однородного уравнения (6)
µ§ - частное решение неоднородного уравнения (6)
µ§
µ§ - общее решение уравнения (6).
µ§
| µ§ |
Рассмотрим функцию:
µ§
µ§ - бесконечно дифференцируема при µ§.
Если µ§ из µ§, то:
µ§
µ§, и при µ§ функция склеивается как бесконечно гладкая.
µ§-финитная :µ§
µ§ - замыкание множества, где µ§ отлична от 0.
µ§.
Введём µ§ - функция n переменных.
Свойства µ§ :
1) µ§- бесконечно дифференцируемая, финитная:
µ§.
2) µ§ - замкнутый шар радиуса h с центром в O.
µ§.
3)µ§
Доказательство.
µ§, С находится из условия µ§.
4) µ§.
Обозначим: µ§
µ§
Интеграл по x бесконечно дифференцируем.
Если µ§, то: µ§
Носитель функции принадлежит области интегрирования, и: µ§.
Если µ§, то µ§ : µ§.
Свойства функции µ§:
µ§
µ§
µ§
µ§
µ§ - срезающая функция.
Пространство µ§.
Определение.
Пусть µ§. Назовём множество функций µ§, пространством µ§, если:
- µ§ - измеримы в Q;
- µ§ в смысле Лебега.
Вводится µ§. Выполняются все аксиомы скалярного произведения.
Утверждение (без доказательства).
µ§ - полное пространство.
Вводится µ§.
Свойства пространства µ§.
Теорема 1.
Множество финитных бесконечно дифференцируемых функций всюду плотно в пространстве µ§ :
µ§.
Доказательство.
Множество ступенчатых функций плотно в µ§.
Множество линейных комбинаций характеристических функций всюду плотно в µ§.
Доказать: любую характеристическую функцию измеримого множества можно сколь угодно точно аппроксимировать финитными функциями.
Любое измеримое множество сколь угодно точно может быть аппроксимировано открытыми областями.
Доказать: характеристическую функцию µ§ можно сколь угодно точно аппроксимировать финитными бесконечно гладкими функциями.
µ§
Рассмотрим µ§ - финитная, бесконечно дифференцируема в µ§.
µ§
Значит, µ§.
µ§
Аппроксимация получена.
Теорема 2.
Множество непрерывных функций всюду плотно в пространстве µ§.
Определение 2.
Пусть µ§ и считается продолженной нулем вне Q µ§. Скажем:
f - непрерывна в среднеквадратичном, если µ§:
µ§.
Теорема 3.
Любая функция из µ§ непрерывна в среднеквадратичном.
Доказательство.
Пусть µ§. Пусть µ§
µ§
Оценим:
µ§
При сдвиге supp сдвигается в пределах шара радиуса 2a.
µ § µ§
Теорема доказана.
Определение 3.
µ§
µ§ - бесконечно дифференцируема, финитна.
Свойства:
µ§
µ§ - осреднение функции f.
Теорема 4.
µ§
Любая функция из µ§ сколь угодно точно аппроксимируема своими осреднениями - бесконечно дифференцируемыми, финитными в µ§.
Доказательство.
µ§
От Q к µ§, от µ§ к µ§
µ§
При µ§.
Возьмем любые две функции:
µ§
Определение.
µ§- множество функций, принадлежащих µ§ на любом компакте внутри области.
µ§
Определение 1.
Пусть µ§
µ§ - обобщённая производная функции f, если µ§ выполняется:
µ§ (1)
Теорема 1.
Обобщённая производная определяется единственным образом.
Доказательство.
Предположим противное: µ§ - обобщённые производные функции f.
µ§ (2)
µ§ (3)
(2),(3) - тождество для µ§
µ§ - что и требовалось доказать.
Теорема 2.
Обобщённые производные не зависят от порядка дифференцирования.
Доказательство - из интегрального тождества (1).
Примеры обобщённых производных.
Ex 1.
µ§
По определению:
µ§
Пусть µ§ и µ§
µ§
| µ§ |
Ex 2.
µ§
Покажем, что обобщённой производной не существует.
Пусть µ§, то:
µ§
где µ§
1) пусть µ§ носитель в µ§, то :
µ§
2) пусть µ§ : µ§, значит:
µ§
Вывод: µ§.
µ§
Вывод: µ§, не имеет обобщённой производной.
Теорема 3.
Пусть µ§ имеет обобщённую производную µ§, то:
1. µ§ (4)
µ§
если µ§.
2. Если к тому же µ§
µ§ (6)
µ§ (7)
Доказательство.
µ§
Выберем h так, чтобы µ§
µ§
Подсказка: если функция финитна, то её носитель - внутри области.
Если функцию умножить на срезающую, то ничего не изменится.
Теорема 4.
µ§
Утверждение.
Пусть µ§, то µ§
µ§
Пусть µ§ - открытый компакт, то µ§ для µ§
µ§
µ§
Теорема 5.
Пусть µ§. µ§ имеет обобщённые производные µ§ и µ§, то
существует обобщённая производная µ§.
Пространство Соболева.
Определение.
µ§, такая, что µ§ называется пространством Соболева порядка k.
µ§
Обозначения: µ§, µ§ или µ§.
Введём µ§.
Утверждение.
µ§ - гильбертово(унитарное, сепарабельное).
Теорема 1.
µ§ - полное пространство.
Доказательство.
µ§ - фундаментальная в µ§ µ§
µ§.
µ§ - мультииндекс
µ§ - может быть равен 0.
µ§
µ§ в µ§.
µ§ в µ§.
Интегральное тождество для µ§:
µ§
Из сильной сходимости следует слабая:
µ§
µ§
Вывод: пространство полное.
Свойства пространств Соболева.
1.µ§ для µ§.
2.Если µ§, то µ§.
3.Если µ§, то µ§.
4.Если µ§, то
µ§
если µ§, то µ§.
5.µ§ - невырожденное, k раз непрерывно дифференцируемое преобразование, отображающее µ§ в µ§.
µ§ и пусть µ§.
Пусть µ§.
Пусть µ§, то µ§.
Утверждение.
Невырожденная, гладкая замена переменных сохраняет принадлежность функции пространству Соболева.
6.Обозначим µ§ - куб со стороной 2a с центром в начале координат.
Множество бесконечно дифференцируемых функций замыкания куба является всюду плотным в µ§.
µ§.
Доказательство.
Раздвинем область, возьмём µ§ и будем её аппроксимировать последовательностью бесконечно гладких функций.
µ§ (определена в растянутом кубе)
µ§
Оценим: µ§
µ§
Выберем µ§ и рассмотрим µ§
µ§
Разбиение единицы.
Теорема.
Пусть µ§ - ограниченная область, пусть µ§ - покрытие замыкания Q, µ§ - может равняться бесконечности.
µ§ - открытые, тогда: существует конечный набо𠵧 - финитные, бесконечно дифференцируемые в µ§, неотрицательные функции, такие, что:
µ§
Используется для локализации свойства: U имеет свойство на µ§, расширяем D на µ§ путём домножения на µ§.
Доказательство.
Возьмём µ§. Для µ§ - y покрывается множеством µ§.
Для каждой выбранной y построим:
µ§
µ§ покрывается µ§. Из бесконечного покрытия выберем конечное подпокрытие:
µ§.
Обозначим: µ§. Обозначим: µ§.
Определим: µ§:
µ§
Получили: µ§.
Если µ§, то µ§, µ§, и µ§.
Знаменатель в 0 не обращается.
Построена
µ§ выполняется свойство 3.
µ§ - выполняются свойства 1 и 2.
Теорема о разбиении единицы доказана.
Теорема о продолжении функции.
Частный случай - продолжение из прямоугольников.
µ§
Продолжение функции из µ§ в µ§.
Лемма 1.
µ§ µ§ - продолжение функции f:
µ§ и µ§
1.Определить функцию.
2.Проверить условие сливания: совпадание значений функции и её производных по µ§ до k-го порядка.
Доказательство.
Определим µ§ (2)
Коэффициенты µ§ из условия:
µ§
µ§ (3)
µ§
Значит, функция непрерывна.
Теперь - доказательство совпадения производных.
µ§
Выполняется одно уравнение из (3), и:
µ§.
Значит: µ§.
Неравенство (1) очевидно через определение нормы в µ§.
Замечание: из доказательства и свойства (6) пространств Соболева следует: можно перейти к µ§ - пространству Соболева с выполнением этой теоремы, и (1) тоже справедливо.
Замечание: в силу того, что множество бесконечно дифференцируемых функций в замыкании куба всюду плотно в пространстве µ§ в этом кубе и в силу того, что протсранство Соболева инвариантно относительно невырожденной гладкой замены переменных.
Лемма 2.
µ§
µ§ (4)
Теорема о продолжении функции.
Пустьµ§ - ограниченная область, граница µ§. Пусть µ§ (µ§- область), тогда:
µ§ - продолжение f, такая, что:
1)µ§
2)µ§
3)µ§ (5)
Замечание.
Лемма 1 - рассмотрены кубики, в теореме: из Q на µ§ и все свойства, как в лемме 1.
Доказательство.
В окрестности каждой точки границы: µ§ нарисуем ша𠵧.
Пусть в O(z) граница задаётся уравнением µ§.
Введём новые переменные:
µ§ - невырожденное преобразование координат.
Преобразование: µ§ - внутри пространства Соболева.
Во что перейдёт множество: µ§
Вырезали куб µ§.
Результат преобразования
Прообраз куба µ§ - криволинейный кубик.
Покроем границу кубиками Vi и выберем конечное подпокрытие.
(Tju)(y) = u(x(y)) (xОVj) - переход от x к y,
переход от y к x : µ§
µ§
Введём : µ§ µ§ если µ§
µ§
µ§ на носителях µ§ обратятся в 1.
µ§
Свойства оператора продолжения:
Похожие работы
... . Являются ли функции ?(x)=cos3x и ?(x)=sin2x на отрезке [pic]. Решить задачу Штурма-Лиувилля y''+?y=0, y(0)=у'(2)=0. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ Билет № 4 3) Какая система функций называется ортогональной в интервале? Приведите примеры. Как решается задача Коши для уравнения теплопроводности с ...
... была построена теория вложения функциональных пространств, которые в настоящее время носят название пространств Соболева. А.Н. Тихоновым была построена теория некорректных задач. Выдающийся вклад в современную теорию дифференциальных уравнений внесли российские математики Н.Н. Боголюбов, А.Н. Колмогоров, И.Г. Петровский, Л.С. Понтрягин, С.Л. Соболев, А.Н. Тихонов и другие. Влияние на развитие ...
... менять саму их постановку, вводя в нее дополнительную априорную информацию о строении решения. 2. Классификация уравнений гиперболического типа в контексте классификации уравнений математической физики Уравнения математической физики, дифференциальные уравнения с частными производными, а также некоторые родственные уравнения иных типов (интегральные, интегро-дифференциальные ...
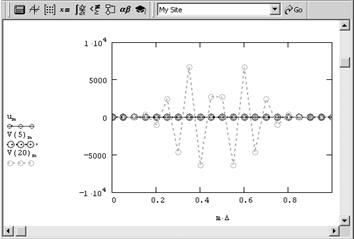
... коэффициенты an (x1), bn (x1), an (x2), bn (x2) при помощи гармонического анализа, можно определить коэффициент температуропроводности стержня а2. Глава 3. МОДЕЛИРОВАНИЕ С ПОМОЩЬЮ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. §3.1. Дифракция излучения на сферической частице. Перейдем теперь к рассмотрению задачи о дифракции электромагнитных волн на сферической частице. Как известно, в ...
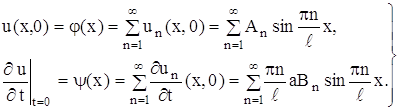
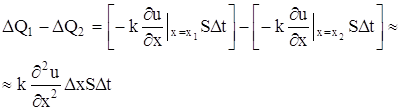
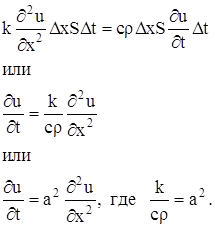
0 комментариев