Основные тригонометрические тождества
![]()
![]()
![]()
![]()
![]()
![]()
Формулы суммы и разности
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Формулы двойного аргумента
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Формулы произведений
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| – a | 90° – a | 90° + a | 180° – a | 180° + a | 270° – a | 270° + a | 360° – a | 360° + a | |
|
|
|
|
|
|
|
|
|
| |
| sin | -sin a | cos a | cos a | sin a | –sin a | –cos a | –cos a | -sin a | sin a |
| cos | cos a | sin a | –sin a | –cos a | –cos a | –sin a | sin a | cos a | cos a |
| tg | -tg a | ctg a | –ctg a | –tg a | tg a | ctg a | –ctg a | –tg a | tg a |
| ctg | -ctg a | tg a | –tg a | –ctg a | ctg a | tg a | -tg a | -ctg a | ctg a |
Формулы понижения степени
![]()
![]()
![]()
![]()
Решения тригонометрических уравнений
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
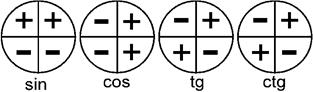
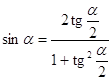
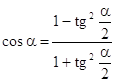
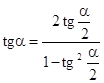
Формулы сокращенного умножения
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
| 0 | 30 | 45 | 60 | 90 | 180 | 270 | 360 |
|
|
| 0 |
|
|
| 1 | 0 | -1 | 0 |
|
|
| 1 |
|
|
|
| -1 | 0 | 1 |
|
|
| 0 |
| 1 |
| – | 0 | – | 0 | При D=0: |
|
| – |
| 1 |
| 0 | – | 0 | – |
|
Похожие работы
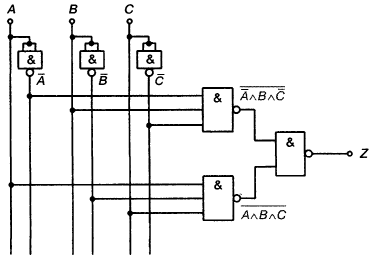
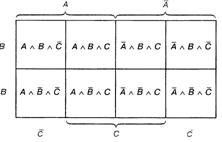
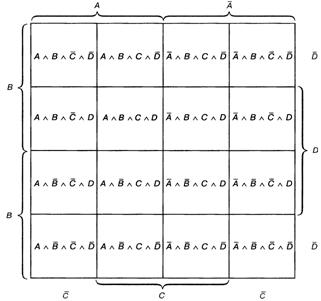
... стовпця відповідає повна кон’юнкція. Якщо в таблиці істинності змінна приймає значення 0, у відповідній повній кон’юнкції вона інвертується. Нормальна кон’юнктивна форма (нормальна форма І) - форма запису рівнянь алгебри логіки, в якій повні диз’юнкції пов’язані між собою логічним множенням. Повна диз’юнкція-операція логічного додавання, в якій беруть участь всі наявні вхідні змінні або їх ...
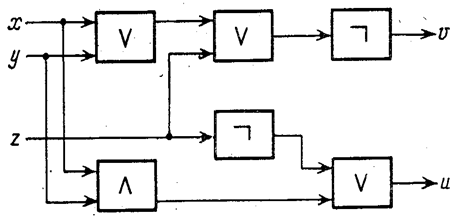
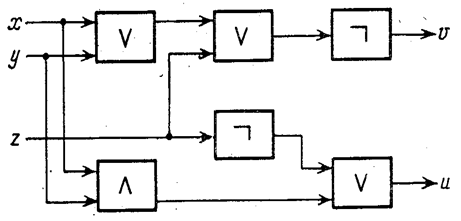
... добавляется бинарная операция деления и (если необходимо) унарная операция взятия обратной величины. Разумеется. при необходимости могут быть введены и другие операции. Особое место в машинной информатике занимает булева алгебра, вводимая на множестве величин типа булевых. Ее основу составляют две бинарные операции: конъюнкция («и»), дизъюнкция («или») и одна унарная операция: отрицание («не»). ...
... бинарная операция деления и (если необходимо) унарная операция взятия обратной величины. Разумеется. при необходимости могут быть введены и другие операции. Особое место в машинной информатике занимает булева алгебра, вводимая на множестве величин типа булевых. Ее основу составляют две бинарные операции: конъюнкция («и»), дизъюнкция («или») и одна унарная операция: отрицание («не»). Конъюнкция ...
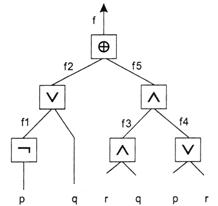
... ответ на этот вопрос положителен. Штрих Шеффера является отрицанием конъюнкции, стрелка Пирса – отрицание дизъюнкции, сумма Жегалкина – отрицание эквивалентности. М. Жегалкин (1869–1947) – российский математик и логик, один из основоположников современной математической логики. Чарльз Пирс (1839–1914) – американский логик, математик и естествоиспытатель. Основоположник семиотики, родоначальник ...
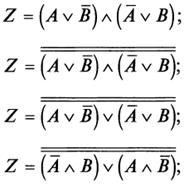

0 комментариев