Навигация
Итоги трансформации
2.2.3 Итоги трансформации
Истекшее с начала 90-х годов время характеризовалось в Венгрии системной трансформацией, охватывающей политические, экономические и внешние отношения.
В политической области сформировалась парламентская республика с ведущей ролью премьер-министра, которым становится лидер победившей на выборах партии, и относительно номинальной ролью президента. В стране отработан и оправдал себя политический механизм смены власти и даже смены системы парламентским путем.
Несмотря на различие политической ориентации сменявших друг друга правительств, в их деятельности наблюдалась определенная преемственность в основных направлениях трансформации - создании правового государства, переходе к рыночной экономике, основанной на частной собственности, переориентации внешнеполитических и внешнеэкономических связей на Запад, под лозунгом "назад в Европу". По всем этим направлениям за минувшие годы был достигнут значительный прогресс.
Политическая стабильность, предсказуемость политики, длительный опыт предшествовавших трансформации экономических реформ сделали Венгрию с самого начала наиболее привлекательной страной для Запада, который охотно вкладывал свои капиталы в эту страну. На протяжении многих лет объем иностранных капиталовложений в венгерскую экономику превышал объем вложений в экономику других стран региона, вместе взятых. Только в последние годы Венгрию стали обгонять в этом отношении Чехия и Польша. Однако по иностранным инвестициям на душу населения (около 2300 долл.) Венгрия по-прежнему лидирует.
В экономической области за эти годы в Венгрии достигнуты большие успехи в создании рыночной экономики. Благодаря длительному периоду предтрансформационных реформ Венгрия смогла быстрее, чем другие страны региона осуществлять системные преобразования.
Так, в 1990 г. был принят закон об установлении цен, который ограничил до необходимого минимума сферу государственного воздействия на цены. В 1991 г. был принят еще ряд важнейших рыночных законов: о недобросовестном поведении на рынке, направленный против монополизма продавца-производителя (закон о конкуренции), об эмиссионном банке, о финансовых институтах, о банкротстве. В эти же годы были приняты законы о приватизации: в 1990 г. Закон о Государственном имущественном агентстве (ГИА) и управлении относящегося к нему имущества, Закон о малой, "предварительной приватизации"; в 1992 г. - ряд дополнительных законов о приватизации, укрепивших ее централизованный характер, и закон о принудительном акционировании. (Единый закон о приватизации, разработка и принятие которого планировались на 1991 г., был принят только в 1995 г.)
Итак, в эти годы было создано правовое поле и институциональная система, в рамках и на основе которых происходило становление рыночного хозяйства. Это был очень важный этап, определивший правила игры в ходе рассматриваемого процесса. Многие венгерские экономисты в начале 90-х годов подчеркивали, что, несмотря на большую продвинутость Венгрии к рынку по сравнению с другими странами региона, она находится лишь в начале пути, что переход к рыночному хозяйству не может быть осуществлен путем "большого скачка", что это процесс, для которого должны быть подготовлены экономические и институциональные предпосылки. В тот момент такой вывод настойчиво подчеркивался и представителями западного мира, напуганными разрушительными последствиями чрезмерно радикальных мер в ряде стран Восточной Европы и России, грозящими, как им тогда казалось, социальными катаклизмами. Так, Ж. Аттали, тогдашний президент ЕБРР, в марте 1992 г. заявил: "Надо заставить понять восточноевропейские страны, что реформы не могут быть осуществлены с одного дня на другой. Сначала надо создать необходимую институциональную систему, что и делалось в Венгрии с 1968г."В те же годы была проведена либерализация импорта (к 1990 г. около 90%), цен (было либерализовано 92%), заработной платы (в 1992 г. было отменено государственное регулирование заработной платы). Характерно, что либерализация цен не вызвала в Венгрии столь разрушительной инфляции, как в других странах региона. Пик инфляции был достигнут в 1991 г., когда темпы роста розничных цен составляли 35%, затем они последовательно снижались, за исключением всплеска в 1995 г., и составили в 1998 г. 14,3%, в 1999 г. - 10, в 2000 г. - 9,8, в 2001 г. - 9,2%.
К 2000 г., по существу, была завершена приватизация. Она началась еще до смены системы, а пик процесса пришелся на 1995-1997 гг. Ее отличительной чертой была преимущественная платность. В середине 1994 г. степень приватизации составила около 50%, при этом доля национальной частной собственности достигла 25-30%, иностранной 15-20%. В этом же году процесс замедлился, поскольку на руках у государства оставались в основном предприятия ключевых отраслей венгерской экономики, приватизация которых была непосильной для отечественных предпринимателей (энергетика, металлургия, тяжелая химия, монополии в области транспорта), и крупные банки. Дальнейшее проведение приватизации требовало серьезных политических решений. Они были приняты пришедшим к власти летом 1994 г. социал-либеральным правительством во главе с социалистами. Был взят курс на ускоренную приватизацию при активном участии иностранного капитала, но с сохранением льгот для отечественного менеджмента и работников[10].
Участие иностранных инвесторов, как правило, транснациональных компаний, обеспечивало вложение дополнительных средств в приватизируемые предприятия и банки. Законом о приватизации, принятом в мае 1995 г., определялись цели, условия и механизм приватизации. Начался процесс приватизации энергетического сектора, телекоммуникационного концерна, важнейших коммерческих банков. Доходы от приватизации были важным источником пополнения государственной казны. Только за один рекордный в истории приватизации 1995 г. государство получило около 4,5 млрд долл., которые пошли на сокращение внешнего долга. В 1997 г. в основном была завершена массированная приватизация, доля частной собственности в экономике превысила 75%. При этом в Венгрии, даже по европейским масштабам, чрезвычайно велика доля иностранного капитала: она составляет более половины в промышленности, около четверти в энергетическом комплексе и более 60% в банковском секторе. Сократилась доля государства в перераспределении доходов: в 1990 г. она составляла 60% ВВП, в 1995 г. - 51, в 1999 г. - 44-45% и столько же в 2000 г. Это соотношение не намного превышает уровень Западной Европы, где оно составляет около 40%2.
После принятия Венгрией нового валютного кодекса МВФ причислил 1 января 1996 г, венгерский форинт к разряду конвертируемых валют.
В 1996-1997 гг. были приняты новые законы в сфере банковской деятельности, рынка ценных бумаг, финансов, учитывающие
изменения в экономике и подготовку к вступлению в ЕС, гармонизирующие ее правовые нормы с нормами европейских стран. Наряду с рынком товаров в Венгрии образовался рынок капитала.
Если в начале 90-х годов происходил трансформационный спад в экономике, обусловленный как переходом к рыночной экономике, так и потерей традиционных восточных рынков в связи с развалом СЭВ и Советского Союза и резкой переориентацией на Запад, то с конца 1995 г. начался период стабилизации.
Спад экономики к 1994 г. закончился, а с середины 1996 г. начался относительно устойчивый рост общественного производства: в 1997 г. темпы роста ВВП составили уже 4,6%, в 1998 г. -4,9, в 1999 г. - 4,1, в 2000 г. - 5,2, в 2001 г. 3,8%, что в условиях ухудшения конъюнктуры в Западной Европе было не мало. В 1996-1997 гг. начала снижаться внешняя задолженность. Венгрия расплатилась с МВФ и перестала брать у него новые кредиты. Норма инфляции упала в 1999 г. до уровня 10%, в 2000 г. она составила 9,8%, в 2001 г. - 9,2%.
После резкого падения жизненного уровня в 1990-1992 гг. и снижения его в 1995 г. наметился рост реальной заработной платы, составивший 4,9% в 1997 г., 3,5% в - 1998 г., 2,5% - в 1999 г. и 1,5% - в 2000 г. (средняя заработная плата превышает 250 долл. в месяц на одного занятого). В 2001 г. повысились темпы роста реальных заработков несмотря на резкое снижение темпов экономического роста - более чем в 4 раза. Это объясняется спецификой предвыборного года. (В апреле 2002 г. в Венгрии прошли новые выборы в парламент страны.) По официальному курсу средний заработок составляет в Венгрии 10% от среднего уровня стран ЕС, а ВВП на душу населения - 20%, по покупательной же способности это соотношение равно 30 и 50%. Улучшилась структура производства и экспорта, более половины объема последнего составляет продукция машиностроения. Благодаря прямым иностранным инвестициям в производство (в 2000 г. около 23 млрд евро) повысилась конкурентоспособность венгерской продукции.
В результате стабилизации улучшились экономические показатели Венгрии. В начале 2002 г. статистическое ведомство Ев-росоюза - Евростат - опубликовало данные о странах претендентах на вступление в ЕС, согласно которым по показателю объема ВВП на душу населения Венгрия находилась на пятом месте среди них. Его уровень равен 51% среднего уровня стран ЕС (Кипр - 86%, Словения - 69, Чехия - 59, Мальта - 56, замыкают ряд Болгария - 28%, Турция - 26 и Румыния -23%).
В 90-е годы развитие страны происходило на фоне политической и экономической ориентации на Запад, что оказывало влияние на характер происходящих процессов. Если в начале 90-х годов продолжалось начатое еще до смены политической системы создание институциональных основ рыночного хозяйства, то вторая половина минувшего десятилетия характеризуется интенсивным продвижением в этом направлении. Если в первой половине десятилетия ощущалось шоковое влияние обвала традиционных рынков и переориентации на более требовательные западные рынки, то во второй половине Венгрии в большей мере, чем другим странам региона удалось адаптироваться к новым условиям. В этот период начались практические шаги по вхождению в европейские интеграционные структуры. Оба процесса ~ переход к рыночной экономике и переориентация экономических связей на Запад, включая будущее вступление в ЕС, - имеют свою социальную и экономическую цену, но они так тесно переплетены друг с другом, что трудно отделить цену перехода к рынку от цены переориентации связей и количественно определить последнюю.
| год | Добавленная стоимость с/х, % от ВВП | Уровень рождаемости, рождений на 1000 чел. | Уровень смертности, смертей на 1000 чел. | Экспорт товаров и услуг, млн.долл.США | Прямые иностранные инвестиции, млн.долл.США | ВВП, млн.долл.США | ВВП на душу населения, долл.США на чел. |
| 1978 | 28,00 | 28,60 | 6,30 | 18974,50 | 0,00 | 190786,00 | 151,00 |
| 1979 | 31,00 | 24,30 | 6,50 | 25800,50 | 0,00 | 206780,00 | 160,00 |
| 1980 | 30,00 | 21,50 | 6,70 | 31524,40 | 0,00 | 221370,00 | 168,00 |
| 1981 | 32,00 | 21,30 | 6,70 | 37985,50 | 0,00 | 236149,00 | 175,00 |
| 1982 | 33,00 | 21,00 | 6,70 | 45588,80 | 542,70 | 254452,00 | 189,00 |
| 1983 | 33,00 | 20,00 | 6,60 | 50966,60 | 802,60 | 279174,00 | 206,00 |
| 1984 | 32,00 | 20,50 | 6,60 | 59495,40 | 1587,60 | 317990,00 | 235,00 |
| 1985 | 28,00 | 20,40 | 6,60 | 50037,40 | 2093,70 | 348785,00 | 261,00 |
| 1986 | 27,00 | 20,60 | 6,60 | 48684,40 | 2366,30 | 380502,00 | 279,00 |
| 1987 | 27,00 | 20,90 | 0,70 | 55554,00 | 2920,30 | 424509,00 | 305,00 |
| 1988 | 26,00 | 22,00 | 6,70 | 61884,80 | 4030,80 | 467271,00 | 332,00 |
| 1989 | 25,00 | 22,10 | 6,70 | 67961,90 | 4282,00 | 484938,00 | 341,00 |
| 1990 | 27,00 | 22,10 | 6,70 | 76460,40 | 4400,60 | 503673,00 | 349,00 |
| 1991 | 24,00 | 21,80 | 6,80 | 91889,20 | 5509,90 | 545529,00 | 376,00 |
| 1992 | 22,00 | 21,50 | 6,90 | 105227,40 | 14078,90 | 614333,00 | 424,00 |
| 1993 | 20,00 | 20,60 | 7,00 | 115003,70 | 34723,90 | 688641,00 | 476,00 |
| 1994 | 20,00 | 19,20 | 7,10 | 148593,20 | 42639,20 | 767536,00 | 532,00 |
| 1995 | 21,00 | 18,30 | 7,30 | 167960,20 | 45241,40 | 839461,00 | 581,00 |
| 1996 | 20,00 | 17,70 | 7,30 | 179481,00 | 50707,20 | 912784,00 | 630,00 |
| 1997 | 19,00 | 17,20 | 7,20 | 228329,40 | 55827,10 | 987831,00 | 679,00 |
| 1998 | 19,00 | 16,60 | 7,10 | 232868,00 | 55213,80 | 1044864,00 | 725,00 |
| 1999 | 18,00 | 16,20 | 7,00 | 252089,60 | 48906,30 | 1112750,00 | 769,00 |
| 2000 | 16,00 | 14,50 | 7,00 | 245668,40 | 46581,40 | 1204922,00 | 824,00 |
КНР
| год | Конечное потребление домашних хозяйств на душу населения, долл.США на чел. | Уровень безграмотности населения, % от общего числа | Импорт товаров и услуг, млн.долл.США | Международный туризм, прибытие на 1000 чел. | Продолжительность жизни, год | Средний возраст населения, год | Чистый уровень миграции, 1 на 1000 чел. |
| 1978 | 77,00 | 37,30 | 20309,44 | 3318,00 | 63,20 | 20,60 | -0,19 |
| 1979 | 82,00 | 35,90 | 28590,82 | 3476,00 | 64,70 | 21,40 | -0,60 |
| 1980 | 89,00 | 34,50 | 32606,12 | 3500,00 | 65,30 | 22,10 | -0,10 |
| 1981 | 96,00 | 33,10 | 36454,63 | 3767,00 | 65,60 | 22,30 | -0,90 |
| 1982 | 102,00 | 31,70 | 37625,53 | 3924,00 | 65,90 | 22,50 | -0,70 |
| 1983 | 110,00 | 30,40 | 46324,42 | 3791,00 | 66,10 | 22,80 | -0,60 |
| 1984 | 124,00 | 29,20 | 59790,97 | 5141,00 | 66,30 | 23,40 | -0,50 |
| 1985 | 140,00 | 37922,00 | 70719,37 | 7133,00 | 66,60 | 23,80 | -0,04 |
| 1986 | 146,00 | 26,90 | 60524,60 | 9000,00 | 66,80 | 24,30 | -0,50 |
| 1987 | 154,00 | 25,80 | 55657,91 | 10760,00 | 66,80 | 24,70 | -0,60 |
| 1988 | 165,00 | 24,80 | 66924,91 | 12361,00 | 66,90 | 24,90 | -0,70 |
| 1989 | 165,00 | 23,90 | 72127,72 | 9361,00 | 67,00 | 25,10 | -0,90 |
| 1990 | 171,00 | 23,00 | 62474,25 | 10484,00 | 67,10 | 25,30 | -0,10 |
| 1991 | 185,00 | 22,20 | 76086,77 | 12464,00 | 6730,00 | 25,60 | -0,12 |
| 1992 | 209,00 | 21,40 | 96909,33 | 16512,00 | 67,40 | 25,80 | -0,12 |
| 1993 | 226,00 | 20,60 | 125236,60 | 18982,00 | 67,70 | 26,30 | -0,15 |
| 1994 | 241,00 | 19,90 | 137595,40 | 19147,00 | 68,10 | 27,40 | -0,17 |
| 1995 | 263,00 | 19,20 | 151869,59 | 20034,00 | 68,20 | 27,60 | -0,22 |
| 1996 | 287,00 | 18,50 | 161132,28 | 22765,00 | 68,50 | 27,90 | -0,24 |
| 1997 | 298,00 | 17,80 | 181148,39 | 23770,00 | 68,90 | 28,30 | -0,27 |
| 1998 | 315,00 | 17,20 | 183654,89 | 25073,00 | 69,50 | 28,80 | -0,29 |
| 1999 | 333,00 | 16,50 | 218980,25 | 27047,00 | 69,70 | 29,60 | -0,31 |
| 2000 | 346,00 | 15,80 | 229579,32 | 19142,00 | 71,00 | 30,00 | -0,25 |
| год | Официальная помощь развитию, млн.долл.США | Личные транспортные средства, шт. на 1000 чел. | Население, тыс.чел. | Плотность населения, чел. на кв.км. | Внешний долг, млн.долл.США | Общее потребление электроэнергии на душу населения, кВт/ч | Уровень безработицы, % от общей раб. силы |
| 1978 | 9,00 | 0,20 | 976926,00 | 104,70 | 3958,60 | 0,33 | 5,3 |
| 1979 | 17,00 | 0,20 | 990387,00 | 106,20 | 4259,10 | 0,33 | 5,1 |
| 1980 | 66,00 | 0,30 | 1003916,00 | 107,60 | 6138,90 | 0,32 | 4,9 |
| 1981 | 477,00 | 0,40 | 1017548,00 | 109,10 | 7316,40 | 0,31 | 3,8 |
| 1982 | 524,00 | 0,60 | 1031251,00 | 110,60 | 10547,90 | 0,32 | 3,2 |
| 1983 | 670,00 | 0,70 | 1045305,00 | 112,10 | 12127,10 | 0,33 | 2,3 |
| 1984 | 798,00 | 0,80 | 1060036,00 | 113,60 | 15247,40 | 0,36 | 1,9 |
| 1985 | 940,00 | 0,80 | 1075631,00 | 115,30 | 21070,40 | 0,38 | 1,8 |
| 1986 | 1097,00 | 0,90 | 1092280,00 | 117,10 | 29933,80 | 0,40 | 2 |
| 1987 | 1382,00 | 1,00 | 1109821,00 | 119,00 | 44598,50 | 0,41 | 2 |
| 1988 | 1924,00 | 1,20 | 1127648,00 | 120,90 | 53558,00 | 0,43 | 2 |
| 1989 | 2077,00 | 1,30 | 1144914,00 | 122,70 | 56704,80 | 0,43 | 2,6 |
| 1990 | 2084,00 | 1,40 | 1161010,00 | 124,50 | 69790,40 | 0,42 | 2,5 |
| 1991 | 1985,00 | 1,60 | 1175705,00 | 126,00 | 76047,10 | 0,43 | 2,3 |
| 1992 | 3046,00 | 1,90 | 1189170,00 | 127,50 | 91404,10 | 0,44 | 2,3 |
| 1993 | 3257,00 | 2,30 | 1201689,00 | 128,80 | 108440,80 | 0,46 | 2,6 |
| 1994 | 3228,00 | 2,60 | 1213726,00 | 130,10 | 126776,60 | 0,65 | 2,8 |
| 1995 | 3531,00 | 2,90 | 1225618,00 | 131,40 | 149029,30 | 0,66 | 2,9 |
| 1996 | 2646,00 | 3,20 | 1237438,00 | 132,70 | 162567,20 | 0,68 | 3 |
| 1997 | 2053,00 | 3,40 | 1249071,00 | 133,90 | 185131,60 | 0,64 | 3 |
| 1998 | 2448,00 | 3,60 | 1260450,00 | 135,10 | 195104,20 | 0,64 | 3,1 |
| 1999 | 2385,00 | 3,90 | 1271460,00 | 136,30 | 194629,10 | 0,61 | 3,1 |
| 2000 | 1735,00 | 4,20 | 1282022,00 | 137,40 | 193781,40 | 0,60 | 3,1 |
Венгрия
| год | Добавленная стоимость с/х, % от ВВП | Уровень рождаемости, рождений на 1000 чел. | Уровень смертности, смертей на 1000 чел. | Экспорт товаров и услуг, млн.долл.США | Прямые иностранные инвестиции, млн.долл.США | ВВП, млн.долл.США | ВВП на душу населения, долл.США на чел. |
| 1968 | 17,00 | 13,10 | 9,80 | 2764,30 | 0,00 | 26420.00 | 2574.00 |
| 1969 | 17,00 | 13,40 | 10,10 | 3259,10 | 0,00 | 28039.00 | 2721.00 |
| 1970 | 17,00 | 14,40 | 10,90 | 4878,60 | 0,00 | 28458,00 | 2753,00 |
| 1971 | 17,00 | 14,40 | 11,20 | 5260,00 | 0,00 | 29429,00 | 2839,00 |
| 1972 | 17,00 | 14,50 | 11,40 | 6504,20 | 0,00 | 32416,00 | 3119,00 |
| 1973 | 17,00 | 14,70 | 11,50 | 7619,60 | 0,00 | 35099,00 | 3363,00 |
| 1974 | 17,00 | 15,40 | 11,70 | 7895,20 | 0,00 | 36636,00 | 3499,00 |
| 1975 | 18,00 | 15,70 | 11,80 | 8254,50 | 0,00 | 37720,00 | 3581,00 |
| 1976 | 18,00 | 15,80 | 12,00 | 8923,70 | 0,00 | 39144,00 | 3697,00 |
| 1977 | 18,00 | 15,80 | 12,40 | 10317,60 | 0,00 | 42094,00 | 3957,00 |
| 1978 | 19,00 | 16,00 | 12,60 | 10524,00 | 0,00 | 41921,00 | 3928,00 |
| 1979 | 19,00 | 16,20 | 12,70 | 11909,00 | 0,00 | 45108,00 | 4216,00 |
| 1980 | 19,00 | 16,30 | 12,80 | 11978,50 | 0,00 | 44958,00 | 4199,00 |
| 1981 | 19,00 | 16,10 | 12,90 | 12619,20 | 0,00 | 46247,00 | 4320,00 |
| 1982 | 20,00 | 14,80 | 13,20 | 13066,00 | 0,00 | 47561,00 | 4449,00 |
| 1983 | 19,00 | 14,10 | 13,60 | 13937,30 | 0,00 | 47905,00 | 4492,00 |
| 1984 | 19,00 | 13,00 | 13,60 | 14862,00 | 0,00 | 49178,00 | 4627,00 |
| 1985 | 18,00 | 12,60 | 13,70 | 15636,10 | 0,00 | 49054,00 | 4637,00 |
| 1986 | 18,00 | 12,40 | 13,70 | 15288,10 | 0,00 | 49807,00 | 4731,00 |
| 1987 | 17,00 | 12,30 | 13,70 | 16014,10 | 0,00 | 51824,00 | 4945,00 |
| 1988 | 17,00 | 12,10 | 13,70 | 17047,30 | 0,00 | 51791,00 | 4959,00 |
| 1989 | 16,00 | 12,10 | 13,80 | 17253,60 | 0,00 | 52172,00 | 5018,00 |
| 1990 | 15,00 | 12,00 | 13,80 | 16331,70 | 0,00 | 50348,00 | 4857,00 |
| 1991 | 9,00 | 12,00 | 13,90 | 14065,40 | 1845,00 | 44360,00 | 4288,00 |
| 1992 | 8,00 | 12,00 | 14,00 | 14361,00 | 1866,50 | 43001,00 | 4165,00 |
| 1993 | 7,00 | 11,90 | 14,00 | 12904,90 | 2965,30 | 42753,00 | 4153,00 |
| 1994 | 7,00 | 11,80 | 14,10 | 14675,50 | 1443,90 | 44013,00 | 4289,00 |
| 1995 | 7,00 | 11,70 | 14,30 | 16643,70 | 5702,50 | 44669,00 | 4366,00 |
| 1996 | 7,00 | 11,50 | 14,30 | 18035,30 | 2869,90 | 45268,00 | 4441,00 |
| 1997 | 6,00 | 11,20 | 14,20 | 22798,40 | 2734,80 | 47338,00 | 4662,00 |
| 1998 | 6,00 | 10,10 | 14,20 | 26605,70 | 2570,80 | 49637,00 | 4908,00 |
| 1999 | 6,00 | 9,90 | 14,10 | 29616,40 | 2461,50 | 51707,00 | 5136,00 |
| 2000 | 6,00 | 8,80 | 13,50 | 3128,30 | 2253,50 | 54371,00 | 5425,00 |
| год | Конечное потребление домашних хозяйств на душу населения, долл.США на чел. | Уровень безграмотности населения, % от общего числа | Импорт товаров и услуг, млн.долл.США | Международный туризм, прибытие на 1000 чел. | Продолжительность жизни, год | Средний возраст населения, год | Чистый уровень миграции, 1 на 1000 чел. |
| 1968 | 0.00 | 2 | 6824,3 | 6257,00 | 68,20 | 33,40 | 0,90 |
| 1969 | 0.00 | 2 | 6986,1 | 6128,00 | 68,60 | 33,20 | 0,70 |
| 1970 | 2024,00 | 1,9 | 7064,53 | 6531,00 | 69,20 | 34,10 | 0,60 |
| 1971 | 2117,00 | 1,9 | 8710,79 | 6018,00 | 69,20 | 34,10 | 0,40 |
| 1972 | 2221,00 | 1,8 | 8289,33 | 6492,00 | 69,20 | 34,10 | 0,30 |
| 1973 | 2353,00 | 1,8 | 8564,52 | 7089,00 | 69,30 | 34,10 | 0,10 |
| 1974 | 2629,00 | 1,7 | 10381,18 | 7562,00 | 69,30 | 34,20 | 0,02 |
| 1975 | 2592,00 | 1,7 | 10947,29 | 7724,00 | 69,30 | 34,20 | -0,15 |
| 1976 | 2655,00 | 1,6 | 11279,96 | 7992,00 | 69,30 | 34,30 | -0,15 |
| 1977 | 2678,00 | 1,6 | 11623,06 | 8245,00 | 69,30 | 34,30 | -0,15 |
| 1978 | 2763,00 | 1,5 | 13373,98 | 8596,00 | 69,40 | 34,40 | -0,15 |
| 1979 | 2813,00 | 1,5 | 12784,83 | 8853,00 | 69,40 | 34,40 | -0,14 |
| 1980 | 2827,00 | 1,4 | 12648,72 | 9413,00 | 69,40 | 34,40 | -0,14 |
| 1981 | 2918,00 | 1,4 | 12852,98 | 10450,00 | 69,30 | 34,50 | -0,23 |
| 1982 | 3000,00 | 1,3 | 12367,82 | 6473,00 | 69,30 | 34,60 | -0,56 |
| 1983 | 3051,00 | 1,3 | 12473,02 | 6764,00 | 69,20 | 34,80 | -0,74 |
| 1984 | 3134,00 | 1,2 | 12608,39 | 8731,00 | 69,20 | 34,90 | -0,96 |
| 1985 | 3170,00 | 1,2 | 13595,40 | 9724,00 | 69,10 | 35,00 | -1,23 |
| 1986 | 3217,00 | 1,1 | 13957,82 | 10613,00 | 69,20 | 35,10 | -1,28 |
| 1987 | 3364,00 | 1,1 | 14364,59 | 11826,00 | 69,30 | 35,30 | -1,52 |
| 1988 | 3305,00 | 1 | 14431,48 | 10563,00 | 69,40 | 35,80 | -1,81 |
| 1989 | 3377,00 | 1 | 14695,59 | 14490,00 | 69,40 | 36,10 | -2,16 |
| 1990 | 3269,00 | 0,9 | 14070,12 | 20510,00 | 69,50 | 36,40 | -2,34 |
| 1991 | 3031,00 | 0,9 | 13212,37 | 21860,00 | 69,40 | 36,70 | -1,83 |
| 1992 | 3017,00 | 0,9 | 13245,00 | 20188,00 | 69,50 | 36,90 | -1,52 |
| 1993 | 3036,00 | 0,8 | 15926,37 | 22804,00 | 69,50 | 37,00 | -1,14 |
| 1994 | 3059,00 | 0,8 | 17334,97 | 21425,00 | 69,50 | 37,20 | -0,57 |
| 1995 | 2901,00 | 0,8 | 17211,39 | 20690,00 | 69,60 | 37,40 | -0,29 |
| 1996 | 2814,00 | 0,7 | 18279,36 | 20674,00 | 69,70 | 37,50 | -0,17 |
| 1997 | 2875,00 | 0,7 | 22779,92 | 17248,00 | 70,20 | 37,70 | -0,05 |
| 1998 | 3031,00 | 0,7 | 27968,96 | 15000,00 | 70,30 | 37,80 | 0,04 |
| 1999 | 3187,00 | 0,6 | 31416,41 | 12930,00 | 70,60 | 38,00 | 0,17 |
| 2000 | 3291,70 | 0,6 | 32159,26 | 12754,00 | 71,90 | 38,10 | 0,20 |
| год | Официальная помощь развитию, млн.долл.США | Личные транспортные средства, шт. на 1000 чел. | Население, тыс.чел. | Плотность населения, чел. на кв.км. | Внешний долг, млн.долл.США | Общее потребление электроэнергии на душу населения, кВт/ч | Уровень безработицы, % от общей раб. силы |
| 1968 | 12,00 | 17,00 | 10261,00 | 111,10 | 0,00 | 1,24 | 18,40 |
| 1969 | 17,00 | 19,00 | 10299,00 | 111,50 | 0,00 | 1,32 | 18,70 |
| 1970 | 24,00 | 25,00 | 10337,00 | 111,90 | 0,00 | 1,43 | 18,00 |
| 1971 | 21,00 | 39,00 | 10375,00 | 112,40 | 0,00 | 1,50 | 17,60 |
| 1972 | 35,00 | 47,00 | 10413,00 | 112,80 | 0,00 | 1,53 | 17,40 |
| 1973 | 48,00 | 52,00 | 10451,00 | 113,20 | 0,00 | 1,65 | 17,50 |
| 1974 | 52,00 | 59,00 | 10490,00 | 113,60 | 0,00 | 1,71 | 16,20 |
| 1975 | 59,00 | 63,00 | 10532,00 | 114,10 | 0,00 | 1,76 | 16,00 |
| 1976 | 60,00 | 74,00 | 10576,00 | 114,50 | 0,00 | 1,85 | 15,80 |
| 1977 | 54,00 | 79,00 | 10621,00 | 115,00 | 54,30 | 1,94 | 15,60 |
| 1978 | 57,00 | 81,00 | 10662,00 | 115,50 | 10405,60 | 2,11 | 15,10 |
| 1979 | 61,00 | 88,00 | 10693,00 | 115,80 | 11189,30 | 2,11 | 14,50 |
| 1980 | 62,00 | 94,60 | 10707,00 | 116,00 | 12321,50 | 2,30 | 14,20 |
| 1981 | 60,00 | 102,30 | 10705,00 | 115,90 | 12349,30 | 2,10 | 13,90 |
| 1982 | 63,00 | 115,60 | 10687,00 | 115,70 | 12867,10 | 2,10 | 13,30 |
| 1983 | 63,00 | 128,20 | 10656,00 | 115,40 | 13547,60 | 2,05 | 12,70 |
| 1984 | 64,00 | 135,90 | 10619,00 | 115,00 | 13872,70 | 2,14 | 12,50 |
| 1985 | 72,00 | 149,50 | 10579,00 | 114,60 | 17613,10 | 2,20 | 12,40 |
| 1986 | 68,00 | 152,10 | 10537,00 | 114,10 | 21338,40 | 2,12 | 12,30 |
| 1987 | 65,00 | 167,60 | 10492,00 | 113,60 | 24715,80 | 2,20 | 12,00 |
| 1988 | 63,00 | 174,50 | 10447,00 | 113,10 | 24747,10 | 2,16 | 11,70 |
| 1989 | 66,00 | 184,20 | 10404,00 | 112,70 | 25740,50 | 2,16 | 11,50 |
| 1990 | 67,00 | 187,50 | 10365,00 | 112,20 | 26756,30 | 2,02 | 11,10 |
| 1991 | 626,00 | 194,80 | 10331,00 | 111,90 | 28560,10 | 1,89 | 10,50 |
| 1992 | 223,00 | 199,40 | 10301,00 | 111,60 | 27799,50 | 1,66 | 9,80 |
| 1993 | 166,00 | 203,20 | 10274,00 | 111,30 | 30746,90 | 1,66 | 11,90 |
| 1994 | 201,00 | 212,20 | 10245,00 | 111,00 | 35682,90 | 1,67 | 10,70 |
| 1995 | 244,00 | 223,20 | 10214,00 | 110,60 | 39866,80 | 1,70 | 10,20 |
| 1996 | 204,00 | 238,80 | 10179,00 | 110,20 | 34336,20 | 1,74 | 9,90 |
| 1997 | 180,00 | 226,20 | 10140,00 | 109,80 | 30914,20 | 1,68 | 8,70 |
| 1998 | 240,00 | 233,80 | 10099,00 | 109,40 | 35727,20 | 1,71 | 7,80 |
| 1999 | 249,00 | 238,40 | 10056,00 | 108,90 | 36651,30 | 1,71 | 7,00 |
| 2000 | 252,00 | 245,60 | 10012,00 | 108,40 | 37125,10 | 1,72 | 6,40 |
Базовый анализ данных включает:
· изучение распределения частот значений переменной (изучение вариационных рядов)
· определение статистик, связанных с распределением частот (среднее арифметическое, мода, медиана, показатели вариации)
· определение показателей формы распределения
· проверку гипотез (гипотез о связях между переменными, гипотезы о различиях)
С распределением частот используют для анализа следующие статистики: среднее арифметическое, мода, медиана, размах межквартирный размах, стандартные отклонения, коэффициент вариации, асимметрия и эксцесс.
Среднеарифметическое используется, когда данные собраны с помощью интервальной или относительной шкалы. Среднее арифметическое определяется по формуле:
,
где Хij – значение i-й переменной по j-му объекту;
n – число объектов в выборке.
Мода – значение переменной, встречающееся чаще других. Мода является хорошим показателем центра распределения. В табл. 3.1 для показателя – доступ к санитарно техническим системам чаще всего встречается значения равное 74 и 78 %.
Медиана – это значение переменной в середине ряда данных, расположенных в порядке возрастания или убывания. В табл. 3.4 представлен показатель – доступ к санитарно техническим системам для выборки в 20 стран в порядке возрастания этого показателя.
Для данных измеряемых с помощью интервальных или относительных шкал определяют следующие показатели вариации:
- рамках вариации;
- межквартальный размах;
- дисперсию;
- стандартное отклонение;
- коэффициент вариации.
Разmах i=Xmaxi ‑ Xmini
Для показателя – городское население (процент от общего населения) Разmах=91-27=64%
Межквартальный размах – это разность между 75 и 25 процентилями.
Среднеквадратическое (стандартное) отклонение определяется по формуле:
.
Коэффициент вариации вычисляется по формуле:
.
Коэффициент вариации определяется для данных, измеряемых с помощью относительной шкалы.
Для базового анализа оценивают закон распределения данных с помощью асимметрии и эксцесса.
Асимметрия – это характеристика распределения, которая оценивает симметрию расположения значений данных относительно средней.
При симметричном распределении значения среднего арифметического, моды и медианы равны между собой, а частоты любых двух значений переменной, которые расположены на одном и том же расстоянии от центра распределения, одинаковы..
Эксцесс (kurtosis)- это показатель, показывающий островершинность или плосковершинность кривой вариационного ряда по сравнению с нормальным распределением.
Эксцесс случайной величины, имеющий нормальный закон распределения, равен нулю. Если эксцесс имеет положительный знак, то распределение более островершинной, при отрицательном знаке более плосковершинной.
Проверка гипотезы заключается в выполнении следующих этапов:
a) формулируется нулевая гипотеза Н0 и альтернативная гипотеза Н1;
b) выбирается статистический критерий проверки гипотезы;
c) выбирается уровень значимости a;
d) определяется объем выборки, собираются данные, вычисляется значение выборочной статистики;
e) определяется вероятность, которую примет статистика критерия (см. этап b) при выполнении нулевой гипотезы, а для альтернативной гипотезы определяется критическое значение статистики, которое делит интервал на область критерия и непринятия нулевой гипотезы;
f) сравнивается полученная вероятность по результатам выборки с заданным уровнем значимости, а для альтернативного варианта определяют, попадет ли выборочное значение в область критерия или отклонения нулевой гипотезы;
g) формулируется решение принять или отвергнуть нулевую гипотезу;
h) излагается статистическое решение с позиций экономического смысла.
Корреляционный анализ
Корреляционный анализ - один из методов статистического анализа взаимозависимости нескольких признаков.
В процессе статистического исследования связей между экономическими явлениями определяют следующие виды коэффициентов корреляции:
a) коэффициент парной корреляции;
b) корреляционное отношение;
c) множественный коэффициент корреляции;
d) частный коэффициент корреляции;
e) коэффициент ранговой корреляции;
f) коэффициент канонической корреляции.
Корреляция – стохастическая (случайная, вероятностная) связь двух или более случайных переменных или рядов данных явлений. При помощи корреляции можно выразить интенсивность и направленность связей между исследуемыми экономическими явлениями.
Самая простая форма корреляции это корреляция между двумя переменными (х и у).
Тесноту линейных связей двух случайных переменных х и у (у= а0+а1х) показывает коэффициент парной корреляции (линейный коэффициент корреляции).
В процессе статистического исследования связей между экономическими явлениями встречаются и такие, в которых корреляция имеет форму кривой, которая может быть гиперболой, параболой и т.д. Степень криволинейной стохастической связи между х и у измеряется корреляционным отношением.
В случае сложных связей между массовыми экономическими явлениями появляется несколько независимых переменных, существенно влияющих на зависимую. Общее влияние этих переменных измеряется с помощью показателей корреляции. Показателем тесноты линейной зависимости случайной переменной у от к случайных переменных х1, х2…хk являет множественный коэффициент корреляции.
Так же рассматривается теснота зависимости между двумя переменными при исключении влияния на эту зависимость остальных переменных. Показателем тесноты зависимости в данном случае является частный коэффициент корреляции.
В некоторых статистических исследованиях существует вероятность того, что некоторые переменные нельзя точно измерить, а даже если такие измерения и получены, есть вероятность того, что в некоторых случаях значения показателей недостоверны. В таких случаях можно проранжировать объекты по значениям показателей одного и второго, получив последовательность. Зависимость между двумя этими последовательностями оценивается коэффициентом ранговой корреляции Спирмана. Коэффициент ранговой корреляции является показателем измерения силы линейной зависимости между двумя наборами рангов.
Корреляционные связи между двумя группами случайных величин оцениваются коэффициентом канонической корреляции. Эта зависимость определяется при помощи новых аргументов канонических величин, вычисленных как линейные комбинации исходных признаков.
Коэффициент парной корреляцииКоэффициент парной корреляции является мерой линейной статистической зависимости между величинами и определяется для генеральной совокупности на основе выборки.
А. Генеральная совокупность с двумя признаками.
Для генеральной совокупности с двумя признаками определяются следующие пять параметров (два математических ожидания, две дисперсии, один коэффициент парной корреляции):
1. Математическое ожидание х: Mx=μx
2. Математическое ожидание у: My=μy
3. Дисперсия х: Dx=σ2x
4. Дисперсия у: Dy=σ2y
5. Коэффициент парной корреляции:
Квадрат коэффициента корреляции называют коэффициентом детерминации.
а) Проверка значимости параметров связи
Значимость коэффициента корреляции показывает зависимость или независимость признаков.
Если коэффициент незначим, то признаки x и y считаются независимыми.
Проверяется гипотеза Н0: r = 0. Для этого вычисляется tнабл.. и находится tтабл.. по таблице t– распределения Стьюдента
tтабл. находится для определенного значения a (a=10%, 5%, 2%, 1%) и n=n-2
Если çtнабл.ç>tтабл., то гипотеза H0 отвергается с вероятностью ошибки a.
Если çtнабл.ç≤tтабл, то гипотеза не отвергается
при n>100 или
б) Интервальная оценка параметров связи
Интервальные оценки обычно находят для значимых параметров связи.
Находим значение статистики Z по формуле
.
Находим точность интервальной оценки по формуле
(t¡ – находится по таблице t-распределения для заданного g)
Интервальная оценка для MZ имеет вид
.
С помощью обратной функции получаем интервальную оценку коэффициента корреляции r (используется таблица Фишера-Иейтса)
Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля (с тем же уровнем a).
Интервальные оценки для коэффициента регрессии получают по формулам:
;
,
где t имеет распределение Стьюдента с n=n-2 степенями свободы.
Примечание. Для значимого коэффициента корреляции некоторые авторы рекомендуют оценку r при небольших выборках
или
для
Регрессионный анализ
Регрессионный анализ используется после того, как с помощью корреляционного анализа выявлено наличие статистически значимых связей между переменными и оценена степень их тесноты.
Регрессионным анализом называется метод статистического анализа зависимости случайной величины у от переменных , рассматриваемых в регрессионном анализе как неслучайные величины, независимо от истинного закона распределения xj.
Предполагается, что случайная величина у имеет нормальный закон распределения с условным математическим ожиданием ỹ, являющимся функцией от аргументов xj и постоянной, не зависящей от аргументов дисперсий s2.
Наиболее часто встречаются следующие виды уравнений регрессии:
‑ линейное многомерное
‑ полином
‑ гипербола
‑ степенное
Полиномиальное, гиперболическое и степенное уравнения приводятся к линейному.
А. Простейшее линейное уравнение регрессии.
а) Оценка уравнения регрессии.
Предполагаем, что в «среднем» у есть линейная функция от х, т.е. уравнение регрессии имеет вид:
,
где ‑ условное математическое ожидание М(у/х);
‑ коэффициенты, которые необходимо оценить по результатам выборочных наблюдений.
Оценить ‑ это значит найти их оценки по выборке (оценки обозначают как в0 и в1). Говорят, что имеем оценку уравнения, т.е. в0 и в1 – найденны, например, методом наименьших квадратов.
Оценка уравнения регрессии записывается в виде:
| Параметры уравнения регрессии | Оценки параметров |
| b0 b1 s2 | в0 в1 s2 |
б) Определение интервальной оценки
где в0 – оценка b0, т.е. Мв0 =b0;
tg ‑ t распределение для уровня значимости a=1-g и числа степеней свободы
v=n-2
в) Проверка значимости b1 (значимости уравнения регрессии)
проверяется гипотеза о равенстве нулю b1 при альтернативной гипотезе
H0: b1=0
H1: b1¹0
Гипотеза H0: b1=0 отвергается с вероятностью ошибки a при выполнении неравенства | t1 |>tкр (a, g=n-2) и уравнение регрессии считается значимым
где ‑ несмещенная оценка среднего квадратического отклонения величины в1;
tкр (a, g=n-2) находится по таблице t-распределения при заданном a и g=n-2
г) Определение интервальной оценки для при заданном х=х0
tv находится по таблице t –распределения Стьюдента для уровня значимости a=1- g и числа степеней свободы v=n-2
Анализ рядов динамикиПоказатели, характеризующие различные объекты и процессы в мировой экономике постоянно меняются во времени, образуя ряды динамики. Такие числовые данные называют так же динамическими или временными рядами. В зависимости от регистрации данных ряды динамики являются дискретными или непрерывными.
Существует несколько классификаций циклов в теории циклов, которая исследует различного рода периодические колебания с различной продолжительностью периодов. Одна из классификаций классифицирует циклы следующим образом:
- длинные волны – период колебаний 40-60 лет;
- средние волны – период 15-20 лет;
- главные циклы – от 6 до 11 лет;
- второстепенные циклы – от 2 до 4 лет;
- сезонные циклы – 2, 3, 4 месяца
Цели анализа рядов динамики следующие:
a) Определить в каком направлении развивается явление: наблюдается ли тенденция возрастания или падения, или значения варьируются вокруг определенного уровня.
b) Выявить причины вариации явления и функцию, описывающую вариации во времени (выявление и измерение периодических колебаний в рядах динамики).
c) Определить какие факторы влияют на вариацию явления, и установить функциональную зависимость показателей, характеризующих явление, от факторов.
d) Осуществить прогнозирование развития явления в будущем.
При анализе рядов динамики встречаются следующие понятия:
- автоковариация;
- автокорреляция;
- тренд;
- тенденция среднего уровня;
- тенденция дисперсии;
- тенденция автокорреляции;
- случайный процесс.
Для использования в рядах динамики корреляционного анализа, регрессионного анализа, ряды динамики необходимо предварительно обработать.
Предварительная обработка рядов динамики заключается в выполнении следующих процедур:a) выявление случайной компоненты ряда динамики;
b) определение тенденции в рядах динамики;
c) выявление сезонной компоненты;
d) выявление основных гармоник;
e) проверка наличия автокорреляции в рядах динамики.
а) Выявление случайной компоненты ряда динамики.
Выявление случайной компоненты – элиминирование (исключение) тенденции из ряда динамики.
Ряд динамики Yt содержит тенденцию Y(t) и случайную компоненту εt
Yt= Y(t) + εt
Тенденция Y(t) представляет собой функцию времени.
Автокорреляцией называется связь между уровнями ряда динамики. Теснота связи оценивается коэффициентом автокорреляции.
,
где RL – коэффициент автокорреляции с лагом L;
Сx(L) = M[()(xi + L –)] ,
где Сx(L) – автокорреляция лага L;
M – значок математического ожидания;
L – временный сдвиг (так же называемый лагом), L = 1,…T
Cx(0) = M[()()] = σ2x
Для исключения тенденции используют различные методы – метод скользящей средней, метод конечных разностей. Ниже изложен метод конечных разностей. Он заключается в том, что последовательно находятся конечные разности. Остатки εtраспределены приблизительно нормально, имеют среднюю 0 и дисперсию σ2.
Основной проблемой является определение порядка разностей, при которых влияние тенденции исключено и разности следующего порядка определять не надо.
Для этого определяют и сравнивают дисперсии.
,
где yt - значение показателя в t-й период времени;
T - количество периодов времени;
Δkyt - конечная разность k–го порядка для t–го периода;
2kCk – биномиальный коэффициент, определяемый из таблиц.
Если определены разности, при которых влияние тенденций исключено, то
Vk≈ Vk+1 ≈ Vk+2 ≈…
В практике ограничиваются определением таких разностей, при которых дисперсии приблизительно равны между собой.
Если V0 ≈ V1 , то конечные разности первого порядка исключают тенденцию и, следовательно, остатки yt1 соответствуют требованиям корреляционного и регрессионного анализа.
b) Определение тенденции в рядах динамики.
Необходимо отметить, что тип функции должен быть адекватен характеру изменения рассматриваемого ряда динамики и должен иметь причинно-следственную обоснованность.
При определении тенденции часто принимают следующие функции:
| полиномы различных порядков | |
| или | ; |
| экспоненциальные функции | |
| или | |
| показательная функция |
Функция, которой соответствует минимальная среднеквадратическая ошибка, является наиболее подходящей.
После определения тренда вычитают значение тренда из соответствующих уровней первоначального ряда динамики и в дальнейшем анализе пользуются отклонениями от тренда.
Если данные не содержат какую-нибудь явную, ярко выраженную тенденцию, то следует начать определение тенденции с самого простого полинома – прямой линии.
c) Подход к выявлению и измерению периодических колебаний в рядах динамики.
В рядах динамики могут содержаться заметные периодические колебания вокруг общей тенденции, для выявления которых следует применить методику анализа, называемую гармоническим анализом.
Задачей гармонического анализа является определение основных гармоник, содержащих основные закономерности развития исследуемого явления. В наиболее продвинутых исследованиях гармонического анализа постулируется, что функцию х(t) можно записать в виде:
x(t) = g(t) + u(t),
где g(t) – периодическая функция;
u(t) – случайная функция времени с нулевым математическим
ожиданием и дисперсией σ2.
Функция g(t) имеет вид:
Найти данную функцию – это значит найти значения ak, bk, T0 (T – период функции, связанный с частотой w зависимостью ).
В частном случае функция g(t) может иметь вид:
Задача выявления периодичности, скрытой в рядах динамики, решается около двухсот лет. Кроме нахождения ak, bk, T, что не представляет серьезных трудностей, для исследователя важным является нахождение причинного механизма, который год за годом, а иногда десятилетия за десятилетием воспроизводит одну и ту же косинусоидальную волну.
Задача решается следующим образом: предполагается, что процесс x(t) хорошо описывается функцией
где A0 – математическое ожидание процесса x(t)
Ak, Bk, wk – неизвестные параметры.
Основным методом нахождения неизвестных параметров Ak, Bk, wk является метод наименьших квадратов, минимизирующий функцию.
Минимум функции достигается решением системы уравнений:
d) Выявление сезонной компоненты.
Выявление сезонной компоненты – это частный случай гармонического анализа, когда T = 12 месяцев.
Процесс описывается функцией вида:
.
Из практики выведено, что n не превышает четырех. Наиболее подходящая функция xk(t) та, у которой дисперсия
σ2 имеет наименьшее значение.
e) Выявление основных гармоник.
С помощью преобразования Фурье любой ряд динамики можно представить в виде суммы конечного числа гармоник. Исследователю не всегда нужны все гармоники, его могут интересовать только те, которые порождают основную часть дисперсии процесса. Задача решается следующим образом.
Функция записывается в виде:
,
где Rk = – амплитуда;
- фаза k-й гармоники.
.
f) Проверка наличия автокорреляции в рядах динамики.
Автокорреляция – это явление, наблюдаемое в рядах динамики, представляющее собой зависимость между последующими и предшествующими членами временного ряда.
Методика корреляционного анализа применяется, когда уровни каждого из взаимосвязанных рядов динамики являются статистически независимыми. Поэтому необходимо проверять наличие автокорреляции, и ее удалять.
В общем случае, когда найден тренд, значения тренда удалены из ряда динамики, предполагаю, что в рядах сформированных из отклонений от тренда, автокорреляции нет. Но нередко при проверке автокорреляция обнаруживается.
Существующие методы для проверки наличия автокорреляции:
- нециклический коэффициент автокорреляции;
- циклический коэффициент автокорреляции;
- критерий Дурбина-Ватсона;
- автокорреляция гармонических рядов.
3 Анализ социально-экономических показателей трансформации
3.3 Расчеты и анализ результатов
3.3.1 Базовый анализ данных
КНР
Рассмотрим показатель- распределение частот уровня рождаемости. Все значения данного показателя принадлежат отрезку [13,3250, 29,7750]. Разобьем отрезок [13,3250, 29,7750] на семь интервалов [(13,3250, 15,6750); (15,6751, 18,0250); (18,0251, 20,3750); (20,3751, 22,7250); (22,7251, 25,0750); (25,0751, 27,4250); (27,4251, 29,7750)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл. 2 представлено распределение частот.
Таблица 2
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | 13,3250 - 15,6750 | 1 | 1 | 4,347826 | 4,347826 |
| 2 | 15,6751 - 18,0250 | 4 | 5 | 17,3913 | 21,73913 |
| 3 | 18,0251 - 20,3750 | 3 | 8 | 13,04348 | 34,78261 |
| 4 | 20,3751 - 22,7250 | 13 | 21 | 56,52174 | 91,30435 |
| 5 | 22,7251 - 25,0750 | 1 | 22 | 4,347826 | 95,65217 |
| 6 | 25,0751 - 27,4250 | 0 | 22 | 0 | 95,65217 |
| 7 | 27,4251 - 29,7750 | 1 | 23 | 4,347826 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 2 представлена гистограмма для показателя – распределение частот уровня рождаемости.
Рис. 2 Гистограмма распределения частот –
распределение частот уровня рождаемости.
Рассмотрим показатель- распределение частот уровня смертности. Все значения данного показателя принадлежат отрезку [0,150000, 7,85000]. Разобьем отрезок [0,150000, 7,85000] на семь интервалов [(0,150000, 1,25000); (1,25001, 2,35000); (2,35001, 3,45000); (3,45001, 4,55000); (4,55001, 5,65000); (5,65001, 6,75000); (6,75001, 7,85000)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл. 3 представлено распределение частот.
Таблица 3
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | 0,150000 - 1,25000 | 1 | 1 | 4,347826 | 4,347826 |
| 2 | 1,25001 - 2,35000 | 0 | 1 | 0 | 4,347826 |
| 3 | 2,35001 - 3,45000 | 0 | 1 | 0 | 4,347826 |
| 4 | 3,45001 - 4,55000 | 0 | 1 | 0 | 4,347826 |
| 5 | 4,55001 - 5,65000 | 0 | 1 | 0 | 4,347826 |
| 6 | 5,65001 - 6,75000 | 12 | 13 | 52,17391 | 56,52174 |
| 7 | 6,75001 - 7,85000 | 10 | 23 | 43,47826 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 3 представлена гистограмма для показателя – распределение частот уровня смертности.
Рис. 3. Гистограмма распределения частот –
распределение частот уровня смертности.
Рассмотрим показатель- распределение частот экспорта товаров и услуг. Все значения данного показателя принадлежат отрезку [-451,76, 271515]. Разобьем отрезок [-451,76, 271515] на семь интервалов [(-451,76 - 38400,7); (38400,8 - 77253,2); (77253,3 - 116105); (116106 - 154958); (154959 - 193810); (193811 - 232663); (232664 - 271515)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл. 4 представлено распределение частот.
Таблица 4
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | -451,76 - 38400,7 | 4 | 4 | 17,3913 | 17,3913 |
| 2 | 38400,8 - 77253,2 | 9 | 13 | 39,13043 | 56,52174 |
| 3 | 77253,3 - 116105 | 3 | 16 | 13,04348 | 69,56522 |
| 4 | 116106 - 154958 | 1 | 17 | 4,347826 | 73,91304 |
| 5 | 154959 - 193810 | 2 | 19 | 8,695652 | 82,6087 |
| 6 | 193811 - 232663 | 1 | 20 | 4,347826 | 86,95652 |
| 7 | 232664 - 271515 | 3 | 23 | 13,04348 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 4 представлена гистограмма для показателя – распределение частот экспорта товаров и услуг.
Рис. 4. Гистограмма распределения частот –
распределение частот экспорта товаров и услуг.
.
Рассмотрим показатель- распределение частот импорта товаров и услуг. Все значения данного показателя принадлежат отрезку [2870,28, 247018]. Разобьем отрезок [2870,28, 247018] на семь интервалов [(2870,28 - 37748,6); (37748,7 - 72626,9); (72627 - 107505); (107506 - 142383); (142384 - 177261); (177262 - 212140); (212141 - 247018)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл.5 представлено распределение частот.
Таблица 5
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | 2870,28 - 37748,6 | 5 | 5 | 21,73913 | 21,73913 |
| 2 | 37748,7 - 72626,9 | 8 | 13 | 34,78261 | 56,52174 |
| 3 | 72627 - 107505 | 2 | 15 | 8,695652 | 65,21739 |
| 4 | 107506 - 142383 | 2 | 17 | 8,695652 | 73,91304 |
| 5 | 142384 - 177261 | 2 | 19 | 8,695652 | 82,6087 |
| 6 | 177262 - 212140 | 2 | 21 | 8,695652 | 91,30435 |
| 7 | 212141 - 247018 | 2 | 23 | 8,695652 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 5 представлена гистограмма для показателя – распределение частот импорта товаров и услуг.
Рис. 5. Гистограмма распределения частот –
распределение частот импорта товаров и услуг.
Рассмотрим показатель- распределение частот ВВП. Все значения данного показателя принадлежат отрезку [106275, 1289433]. Разобьем отрезок [106275, 1289433] на семь интервалов [(106275 - 275297); (275298 - 444320); (444321 - 613342); (613343 - 782365); (782366 - 951388); (951389 - 1120411); (1120412 - 1289433)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл. 6 представлено распределение частот.
Таблица 6
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | 106275 - 275297 | 5 | 5 | 21,73913 | 21,73913 |
| 2 | 275298 - 444320 | 5 | 10 | 21,73913 | 43,47826 |
| 3 | 444321 - 613342 | 4 | 14 | 17,3913 | 60,86957 |
| 4 | 613343 - 782365 | 3 | 17 | 13,04348 | 73,91304 |
| 5 | 782366 - 951388 | 2 | 19 | 8,695652 | 82,6087 |
| 6 | 951389 - 1120411 | 3 | 22 | 13,04348 | 95,65217 |
| 7 | 1120412 - 1289433 | 1 | 23 | 4,347826 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 6 представлена гистограмма для показателя – распределение частот ВВП.
Рис. 6. Гистограмма распределения частот –
распределение частот ВВП.
Рассмотрим показатель- распределение частот численности населения. Все значения данного показателя принадлежат отрезку [951501, 1307447]. Разобьем отрезок [951501, 1307447] на семь интервалов [(951501 -1002351); (1002352 - 1053200); (1053201 - 1104049); (1104050 - 1154899); (1154900 - 1205748); (1205749 - 1256597); (1256598 - 1307447)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл. 7 представлено распределение частот.
Таблица 7
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | 951501 -1002351 | 2 | 2 | 8,695652 | 8,695652 |
| 2 | 1002352 - 1053200 | 4 | 6 | 17,3913 | 26,08696 |
| 3 | 1053201 - 1104049 | 3 | 9 | 13,04348 | 39,13043 |
| 4 | 1104050 - 1154899 | 3 | 12 | 13,04348 | 52,17391 |
| 5 | 1154900 - 1205748 | 4 | 16 | 17,3913 | 69,56522 |
| 6 | 1205749 - 1256597 | 4 | 20 | 17,3913 | 86,95652 |
| 7 | 1256598 - 1307447 | 3 | 23 | 13,04348 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 7 представлена гистограмма для показателя – распределение частот уровня численности населения.
Рис. 7. Гистограмма распределения частот –
распределение частот численности населения.
Венгрия
Рассмотрим показатель- распределение частот уровня рождаемости. Все значения данного показателя принадлежат отрезку [8,17500, 16,9250]. Разобьем отрезок [8,17500, 16,9250] на семь интервалов [(8,17500 - 9,42500); (9,42501 - 10,6750); (10,6751 - 11,9250); (11,9251 - 13,1750); (13,1751 - 14,4250); (14,4251 - 15,6750); (15,6751 - 16,9250)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл.8 представлено распределение частот.
Таблица 8
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | 8,17500 - 9,42500 | 1 | 1 | 3,030303 | 3,030303 |
| 2 | 9,42501 - 10,6750 | 2 | 3 | 6,060606 | 9,090909 |
| 3 | 10,6751 - 11,9250 | 5 | 8 | 15,15152 | 24,24242 |
| 4 | 11,9251 - 13,1750 | 10 | 18 | 30,30303 | 54,54545 |
| 5 | 13,1751 - 14,4250 | 4 | 22 | 12,12121 | 66,66667 |
| 6 | 14,4251 - 15,6750 | 4 | 26 | 12,12121 | 78,78788 |
| 7 | 15,6751 - 16,9250 | 7 | 33 | 21,21212 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 8 представлена гистограмма для показателя – распределение частот уровня рождаемости.
Рис. 8. Гистограмма распределения частот –
распределение частот уровня рождаемости.
Рассмотрим показатель- распределение частот уровня смертности. Все значения данного показателя принадлежат отрезку [9,4250, 14,6750]. Разобьем отрезок [9,4250, 14,6750] на семь интервалов [(9,4250 -10,1750); (10,1751 - 10,9250); (10,9251 - 11,6750); (11,6751 - 12,4250); (12,4251 - 13,1750); (13,1751 - 13,9250); (13,9251 - 14,6750)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл. 9 представлено распределение частот.
Таблица 9
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | 9,4250 -10,1750 | 2 | 2 | 6,060606 | 6,060606 |
| 2 | 10,1751 - 10,9250 | 1 | 3 | 3,030303 | 9,090909 |
| 3 | 10,9251 - 11,6750 | 3 | 6 | 9,090909 | 18,18182 |
| 4 | 11,6751 - 12,4250 | 4 | 10 | 12,12121 | 30,30303 |
| 5 | 12,4251 - 13,1750 | 4 | 14 | 12,12121 | 42,42424 |
| 6 | 13,1751 - 13,9250 | 11 | 25 | 33,33333 | 75,75758 |
| 7 | 13,9251 - 14,6750 | 8 | 33 | 24,24242 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 9 представлена гистограмма для показателя – распределение частот уровня смертности.
Рис. 9 Гистограмма распределения частот –
распределение частот уровня смертности.
Рассмотрим показатель- распределение частот экспорта товаров и услуг. Все значения данного показателя принадлежат отрезку [526,625, 31854]. Разобьем отрезок [526,625, 31854] на семь интервалов [(526,625 - 5001,97); (5001,98 - 9477,32); (9477,33 - 13952,6); (13952,7 - 18428,0); (18428,1 - 22903,3); (22903,4 - 27378,7); (27378,8 - 31854,0)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл. 10 представлено распределение частот.
Таблица 10
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | 526,625 - 5001,97 | 4 | 4 | 12,12121 | 12,12121 |
| 2 | 5001,98 - 9477,32 | 6 | 10 | 18,18182 | 30,30303 |
| 3 | 9477,33 - 13952,6 | 8 | 18 | 24,24242 | 54,54545 |
| 4 | 13952,7 - 18428,0 | 12 | 30 | 36,36364 | 90,90909 |
| 5 | 18428,1 - 22903,3 | 1 | 31 | 3,030303 | 93,93939 |
| 6 | 22903,4 - 27378,7 | 1 | 32 | 3,030303 | 96,9697 |
| 7 | 27378,8 - 31854,0 | 1 | 33 | 3,030303 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 10 представлена гистограмма для показателя – распределение частот экспорта товаров и услуг.
Рис. 3.3.9 Гистограмма распределения частот –
распределение частот экспорта товаров и услуг.
Рассмотрим показатель- распределение частот импорта товаров и услуг. Все значения данного показателя принадлежат отрезку [4713,05, 34270,5]. Разобьем отрезок [4713,05, 34270,5] на семь интервалов [(4713,05 - 8935,54); (8935,55 - 13158,0); (13158,1 - 17380,5); (17380,6 - 21603,0); (21603,1 - 25825,5); (25825,6 - 30048,0); (30048,1 - 34270,5)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл. 11 представлено распределение частот экспорта товаров и услуг.
Таблица 11
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | 4713,05 - 8935,54 | 6 | 6 | 18,18182 | 18,18182 |
| 2 | 8935,55 - 13158,0 | 10 | 16 | 30,30303 | 48,48485 |
| 3 | 13158,1 - 17380,5 | 12 | 28 | 36,36364 | 84,84848 |
| 4 | 17380,6 - 21603,0 | 1 | 29 | 3,030303 | 87,87879 |
| 5 | 21603,1 - 25825,5 | 1 | 30 | 3,030303 | 90,90909 |
| 6 | 25825,6 - 30048,0 | 1 | 31 | 3,030303 | 93,93939 |
| 7 | 30048,1 - 34270,5 | 2 | 33 | 6,060606 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 11 представлена гистограмма для показателя – распределение частот импорта товаров и услуг.
Рис. 11 Гистограмма распределения частот –
распределение частот импорта товаров и услуг.
Рассмотрим показатель- распределение частот ВВП. Все значения данного показателя принадлежат отрезку [-4422,6, 58893,5]. Разобьем отрезок [-4422,6, 58893,5] на семь интервалов [(-4422,6 - 4622,58); (4622,59 - 13667,7); (13667,8 - 22712,9); (22713 - 31758,0); (31758,1 - 40803,2); (40803,3 - 49848,4); (49848,5 -58893,5)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл. 12 представлено распределение частот.
Таблица 12
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | -4422,6 - 4622,58 | 2 | 2 | 6,060606 | 6,060606 |
| 2 | 4622,59 - 13667,7 | 0 | 2 | 0 | 6,060606 |
| 3 | 13667,8 - 22712,9 | 0 | 2 | 0 | 6,060606 |
| 4 | 22713 - 31758,0 | 2 | 4 | 6,060606 | 12,12121 |
| 5 | 31758,1 - 40803,2 | 5 | 9 | 15,15152 | 27,27273 |
| 6 | 40803,3 - 49848,4 | 18 | 27 | 54,54545 | 81,81818 |
| 7 | 49848,5 -58893,5 | 6 | 33 | 18,18182 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 12 представлена гистограмма для показателя – распределение частот ВВП.
Рис. 12 Гистограмма распределения частот –
распределение частот ВВП.
Рассмотрим показатель- распределение частот численности населения. Все значения данного показателя принадлежат отрезку [9954,08, 10764,9]. Разобьем отрезок [9954,08, 10764,9] на семь интервалов [(9954,08 - 10069,9); (10070 - 10185,7); (10185,8 - 10301,5); (10301,6 - 10417,4); (10417,5 - 10533,2); (10533,3 - 10649,0); (10649,1 - 10764,9)]. Определим число лет, попавших в каждый интервал, процент показавших в каждый, процент годов попавших в каждый интервал с учетом пропусков и накопленные проценты. В табл. 13 представлено распределение частот.
Таблица 13
Распределение частот
| № интервала | Значение интервала | Частоты, число объектов в интервале | Частоты, % | Достоверные частоты, % | Накопленные частоты, % |
| 1 | 9954,08 - 10069,9 | 2 | 2 | 6,060606 | 6,060606 |
| 2 | 10070 - 10185,7 | 3 | 5 | 9,090909 | 15,15152 |
| 3 | 10185,8 - 10301,5 | 6 | 11 | 18,18182 | 33,33333 |
| 4 | 10301,6 - 10417,4 | 6 | 17 | 18,18182 | 51,51515 |
| 5 | 10417,5 - 10533,2 | 5 | 22 | 15,15152 | 66,66667 |
| 6 | 10533,3 - 10649,0 | 5 | 27 | 15,15152 | 81,81818 |
| 7 | 10649,1 - 10764,9 | 6 | 33 | 18,18182 | 100 |
В третьей колонке показано количество лет, попавших в соответствующий интервал. В четвертой колонке процент годов, попавших в интервал. В пятой колонке проценты, подсчитанные с учетом отсутствующих значений. В последнем столбце показаны накопленные частости с учетом пропусков. На рис. 13 представлена гистограмма для показателя – распределение частот численности населения.
Рис. 13. Гистограмма распределения частот –
распределение частот численности населения.
Похожие работы
... образования не в полной мере нацелено на цели и задачи экономических реформ, и вместе с тем, в недостаточной мере предпринимаются шаги для совершенствования управления образовательным фактором экономического роста Павлодарской области. В частности, из данных, приведенных в подразделе 2 раздела 2, мы видим, что для Павлодарского региона характерна проблема снижения численности населения, и только ...
... российских инвестиций в объекты экономики Украины и украинских – в Россию, а также проведение работы по активному развитию российско-украинских торгово-экономических связей на межрегиональном уровне.[59] 2.2. Тенденции, проблемы и перспективы развития российско-украинских экономических отношений. Среди стран СНГ Украина – потенциально наиболее важный и одновременно один из наиболее сложных ...
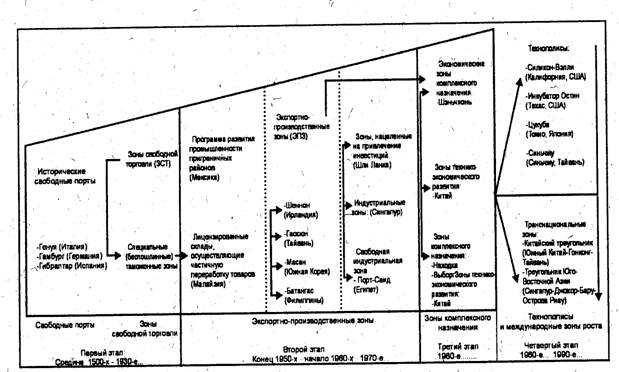
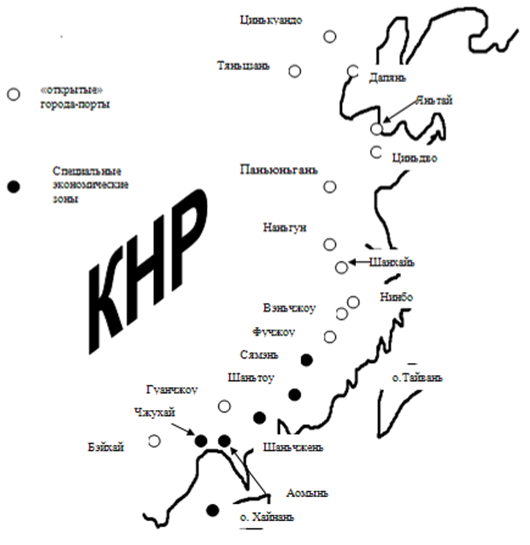
ложения соответствующей фирмы в стране. Примером реализации первого подхода являются свободные экономические зоны Китая, зона «Манаус» (Бразилия), многие экспортно-производственные зоны в развивающихся странах. Результатом второго подхода являются «точечные» зоны, представленные отдельным предприятиям (оффшорные фирмы, магазины «дьюти фри»). Одной из простейших форм свободных экономических зон ...
... о СЭЗ. На федеральном уровне в статье 23 Федерального закона "О государственном регулировании внешнеторговой деятельности" от 13.10. 1995 №157-ФЗ (в редакции Федеральных законов от 08.07.97 №96-ФЗ, от 10.02.99 №32-ФЗ) свободная экономическая зона определяется как особый режим осуществления отдельных видов внешнеторговой деятельности, при этом дается ссылка на федеральный закон "О свободных ...


0 комментариев