Навигация
Формирование исходной популяции
25665
знаков
1
таблица
5
изображений
3.2 Формирование исходной популяции
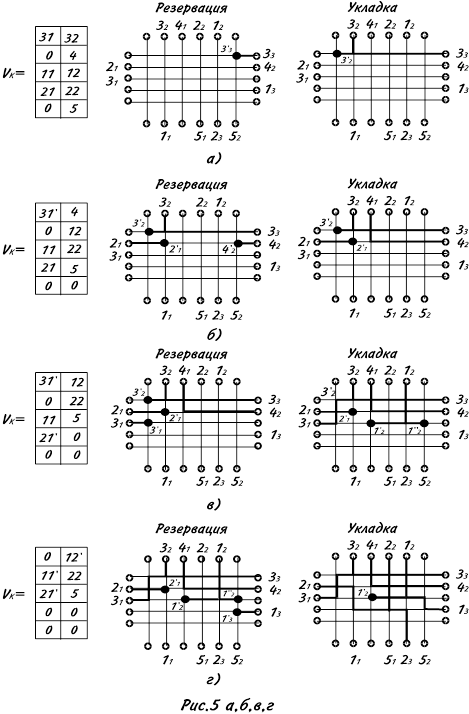
Для организации генетического поиска формируется исходная популяция особей P={Hi|i=1,2,..,M}, где М размер популяции. Популяция Р- представляет собой репродукционную группу – совокупность индивидуальностей, любые две из которых HiÎP и HjÎP, i ¹ j могут размножаться выступая в роли «родителей». Предварительно с помощью процедуры FORM осуществляется разбиение КП на области и формирование модели КП в виде графа W=(X,U). Далее для каждой цепи ti Î Т строится алгоритмом Прима один из вариантов минимального связывающего дерева Di={ri, li=1, … ni}
Затем для каждого rij синтезируется набор Vij вариантов маршрутов в ортогональном графе G, реализующих ребро rij. Пусть nij=| Vij |- число вариантов реализации ребра rij.
Определяется длина L хромосомы, являющейся носителем информации о конкретном решении:
Параметр L определяет число генов в хромосоме. С помощью графика соответствия Q устанавливается соответствие Г(G, Q, R) между генами хромосомы и ребрами минимальных связывающих деревьев для всех цепей.
G={gn| n=1, 2,… ,L}; R={rij| i=1, 2, … ,ni, j=1,2, … ni}
Образом Г(rij) является ген gn. Прообразом Г-1(gn) является ребро rij Значением гена gn, будет номер варианта реализации ребра rij=Г-1(gn) .
Ген gn может принимать любое значение от 1 до nij.
В работе используется принцип случайного формирования исходной популяции.
Для этого в пределах каждой хромосомы Нк каждый ген gn принимает случайное значение в пределах от 1 до nij , где nijчисло вариантов реализации ребра rij=Г-1(gn).
Управляемыми параметрами при формировании популяции является М - размер популяции, nmax - максимальное число вариантов реализации ребер, т.е. ("ij) [nij
nmax]. Если возможное число вариантов nij больше nmax то возникает возможность формирования альтернативных наборов вариантов Vij для rij. Кроме того существует возможность построения альтернативных МСД Di для одной и той же цепи ti.
Все это дает возможность для комбинирования при синтезе исходной популяции. Известно, что для выхода из локальных оптимумов используется механизм смены исходных популяций.
В простейшем случае это можно реализовать с помощью повторной, случайной генерации.
3.3 Генетические операторы
Для получения нового решения (индивидуальности) используются генетические операторы: кроссинговер и мутация.
Кроссинговер заключается во взаимном обмене генами между «родителями» - хромосомами предварительно выбранной пары.
В нашем случае все хромосомы гомологичны, т.к. имеют одну и ту же структуру, одну и ту же длину и несут информацию об одном и том же наборе МСД. Гены, расположенные в одном и том же локусе хромосом, гомологичны, т.к. несут информацию об одном и том же ребре хромосомы.
Предварительно задается величина PK – вероятность кроссинговера и вводится флажок FG с двумя состояниями «выполнять», «не выполнять». Исходное состояние FG «не выполнять». При выполнении кроссинговера последовательно просматриваются локусы выбранной пары хромосом. С вероятностью Pk «флажок» FG переходит в состояние «выполнять». Если FG перешел в состояние «выполнять», то производится обмен генами между парой хромосом в текущем локусе, далее «флажок» переходит в состояние «не выполнять», а затем осуществляется переход к следующему локусу.
Такой алгоритм кроссинговера обеспечивает мультиобмен. Число пар обменивающихся генов определяется параметром Pk.
Операция мутации заключается в изменении значения гена. Алгоритм мутации реализуется следующим образом.
Предварительно, для каждого гена gn, определяется диапазон его возможных значений от 1 до yn, где yn – число сформированных вариантов реализации ребра 
.
Задается параметр PM – вероятность мутации и «флажок» FG с двумя состояниями «выполнять» и «не выполнять». Исходное состояние FG – «не выполнять».
Последовательно выбираются хромосомы из текущей популяции. В пределах выбранной хромосомы последовательно просматриваются гены. После перехода к очередному гену, FG с вероятностью PM переходит в состояние «выполнять». Если FG перешел в состояние «выполнять», то случайным образом ген gn принимает одно из значений в заданном диапазоне, за исключением значения, которое ген имеет перед мутацией. Далее FG переходит в состояние «не выполнять» и выбирается следующий ген хромосомы, или следующая хромосома.
Для улучшения процесса поиска лучшего решения введем дифференцируемое значение показателя 
, принимающего различные значения в зависимости от значения гена.
Введем для гена gn оценку 
, где ln – число ребер ui, входящих в маршрут vijk реализующий ребро , соответствующее гену gn. 
- число таких ui,, входящих в vijk ,для которых показатель загрузки ci имеет отрицательное значение.
Кn меняется от 0 до 1. Чем больше Kn, тем “хуже” маршрут vijk, и тем больше оснований к его смене.
Значение показателя с учетом Кn для гена gn определяется следующим образом
параметр D связан с Pm следующим соотношением
,
т.е. D меняется от 0 до (1-Pm).
В предельном случае
Как видно из алгоритмов, реализующих процедуры кроссинговера и мутации, временная сложность операторов кроссинговера и мутации применительно к одной хромосоме имеют линейную зависимость, 
, где L – длина хромосомы.
Похожие работы
... оценкой качества служит критерий: где li суммарная длина реализованной (протрассированной) цепи ni и L - суммарная длина всех цепей. 2. Генетический алгоритм трассировки в коммутационном блоке Особенностью генетического алгоритма, моделирующего процесс естественной эволюции, является то, что оперирование производится с кодами решений. Каждому решению соответствует одна ...
... производительных сил, тем быстрее повышается Б. населения. В еще большей степени Б. связано с эффективностью социально-экономической политики в данном обществе. Информатика как наука. Предмет и объект прикладной информатики. Системы счисления Инфоpматика — это основанная на использовании компьютерной техники дисциплина, изучающая структуру и общие свойства информации, а также закономерности и ...
... ребрами) изображают конструктивные и потоковые функциональные структуры [14]. Принципы построения функциональных структур технических объектов рассматриваются в последующих главах курса "Основы проектирования им конструирования" не включенных в настоящее пособие. Для систем управления существуют характеристики, которые можно использовать в качестве критериев для оценки структур. Одна из них - ...
... обучения, yi и yj –выходные сигналы i-го и j-го нейронов. В настоящее время существует множество разнообразных обучающих правил (алгоритмов обучения). Глава IV Может ли компьютер мыслить? 4.1 Реально ли компьютерное мышление? Наконец я подошел к заключительной главе своей работы. В предыдущих главах была изложена сущность построения систем искусственного интеллекта, было рассказано о ...
0 комментариев