Навигация
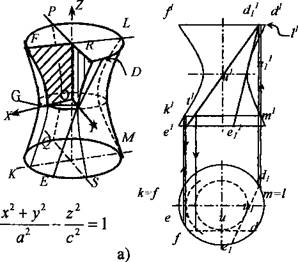
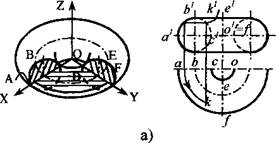
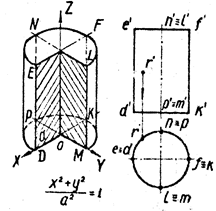
Однополостный гиперболоид образуют вращением прямой ED вокруг скрещивающейся с ней оси Z (рис. 3)
3. Однополостный гиперболоид образуют вращением прямой ED вокруг скрещивающейся с ней оси Z (рис. 3).
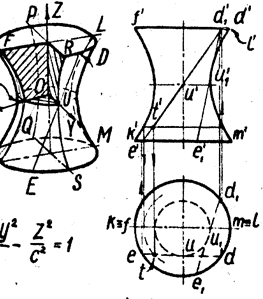
Плоскости XOZ и YOZ пересекают его по гиперболам FK, LM, PQ и RS, а плоскость XOY и ей параллельные – по окружностям (GU, FPLR и KQMS). При вращении точек D и Е их проекции d и е перемещаются по окружности, а проекции d и e – по прямым, параллельным оси Х. Точка U прямой DE, ближе других расположенная к оси вращения, описывает окружность UU1 наименьшего диаметра. Эту окружность называют горлом поверхности. Лучи, проектирующие какую-либо поверхность, касаются её в точках, образующих контурную линию. Соответствующая проекция этой линии называется очерком поверхности.
Форму однополостного гиперболоида имеютнекоторые радиомачты. Он также образует форму вибрационных питателей, используемых в промышленной автоматике, кулачков, соединителей контактов и так далее.
Поверхности вращения нелинейчатые.К этому классу относят в основном поверхности, образованные вращением кривых второго порядка.
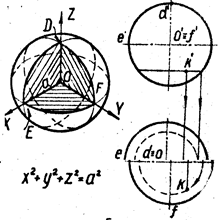 |
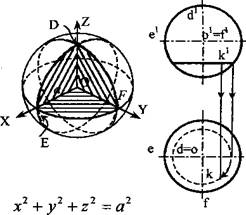
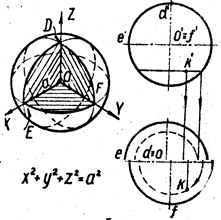
1. Сферу образуют вращением окружности вокруг её диаметра (рис. 4). Любая плоскость пересекает сферу по окружности. Очерк фронтальной проекции сферы называют главным меридианом, очерк горизонтальной проекции – экватором. Проекции точки К, лежащей на поверхности сферы, принадлежат проекциям горизонтальной окружности, проведённой на сфере. Рис. 4
Сфера образует форму диаграммы направленности антенн, обтекателя и излучателя антенны, головки микрофона, контактов реле и так далее. Сфера является поверхностью положения объекта в пространстве.
2. Круговой тор образуют вращением окружности вокруг оси, лежащей в плоскости этой окружности и не являющейся её диаметром. Таким образом, сферу можно рассматривать как частный случай тора. Различают тор-кольцо, когда ось вращения не пересекает образующую окружность, и тор-бочку.
В радиотехнике используют также параболический и эллиптический тор.
Параболический тор образуют вращением параболы вокруг прямой, лежащей в плоскости этой параболы и не являющейся её фокальной осью.
Эллиптический тор образуют вращением эллипса вокруг прямой, лежащей в плоскости этого эллипса и не являющейся его осью.
Торовые поверхности имеют диаграммы направленности антенн, поверхности положения объекта в пространстве, антенны и их обтекатели, волноводы, резонаторы, громкоговорители и так далее.
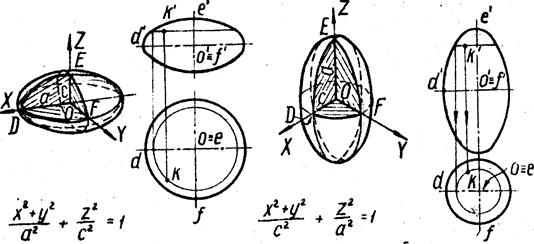
3. Эллипсоид образуют вращением эллипса вокруг его малой или большой оси. В первом случае получают сжатый (рис. 5, а), а во втором – вытянутый эллипсоиды вращения (рис. 5, б).
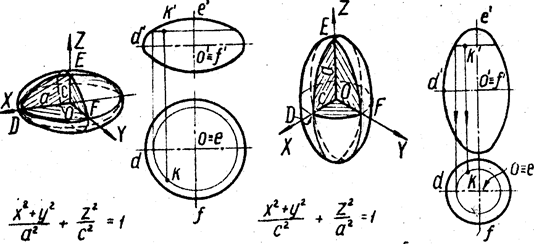
Рис. 5 а) б)
Плоскости XOZ и YOZ пересекают их по эллипсам DE и EF, а плоскость XOY – по окружности DF.
Форму эллипсоида имеют зеркала антенн и лазеров, излучатели антенн, поверхности положения и так далее.
4. Двуполостный гиперболоид образуют вращением гиперболы DE вокруг её действительной оси FF1 (рис. 6).
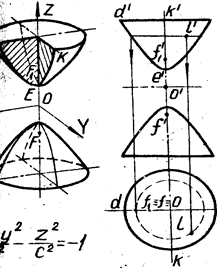 |
Рис. 6
Плоскости XOZ и YOZ пересекают его по гиперболам DE и KE; плоскость XOY даёт в сечении мнимую точку О.
Форму его имеют зеркала антенн, поверхности положения объекта в пространстве и так далее.
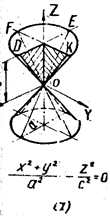
5. Параболоид образуют вращением параболы OD вокруг её фокальной оси OF (рис. 7).
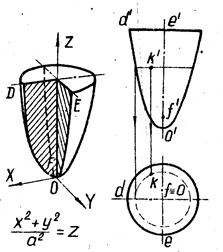
Рис. 7
Зеркала антенн и лазеров чаще всего изготовляют параболическими.
6. Поверхность вращения общего вида образуют вращением произвольной кривой.
Поверхности с плоскостью параллелизма.
Все поверхности этого класса – линейчатые.
1. Цилиндроид образуют перемещением прямой по двум кривым направляющим, когда образующая остаётся параллельной заданной плоскости. Форму цилиндроида имеют некоторые объёмные графики, применяемые в теории оптимального регулирования, а также волноводы.
2. Коноид образуют перемещением прямой по кривой линии и прямой, когда образующая остаётся параллельной заданной плоскости. Частным случаем коноида является прямой геликоид, образуемый перемещением прямой по винтовой линии и её оси, когда образующая остаётся параллельной заданной плоскости.
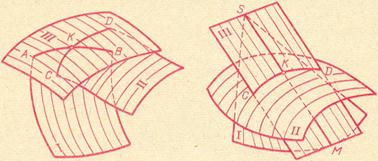
3. Гиперболический параболоид или косую плоскость образуют перемещением прямой по двум скрещивающимся прямым, когда образующая остаётся параллельной некоторой плоскости. Получаемая поверхность имеет седлообразную форму (рис. 8).
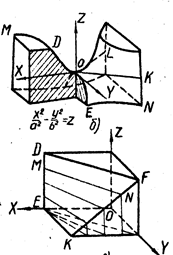 |
Рис. 8
Плоскости XOZ и YOZ пересекают эту поверхность по параболам OD и OE; плоскости параллельные XOZ и YOZ ,также дают в сечении параболы; плоскость XOZ пересекает поверхность по двум пересекающимся прямым OL и OK, а плоскости, параллельные XOZ,- по гиперболам (EN и DM).
Поверхности, задаваемые каркасом.
К ним относятся поверхности, образование которых не подчинено определённому геометрическому закону. Эти поверхности задают каркасом – семейством линий, принадлежащих им и параллельных координатным плоскостям ( рис. 9).
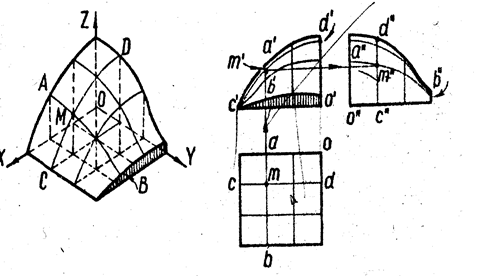 |
Рис. 9
На рис. 9 изображён объёмный график, используемый в радиотехнике. Поверхность определена кривыми линиями, одно семейство которых (CD) параллельно плоскости XOZ, а другое (АВ) – плоскости YOZ. Точка М поверхности определена как точка пересечения кривых АВ и CD.
В радиоэлектронике и автоматике встречаются поверхности второго порядка общего вида: эллиптические конус и цилиндр, параболический и гиперболический цилиндры и так далее.
Пространственные кривые линии.
Если кривую линию без её деформации нельзя совместить всеми точками с плоскостью, то её называют пространственной. К таким кривым относят винтовые линии.
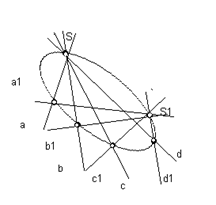
Винтовая линия – это траектория движения точки, равномерно перемещающейся вдоль образующей, которая равномерно вращается вокруг оси этой поверхности. Винтовую линию называют правой, если на видимой стороне поверхности она идёт слева вверх направо (рис. 10, а); в противном случае её называют левой (рис. 10, б).
Расстояние S, которое проходит точка вдоль образующей за один её оборот, называют шагом винтовой линии. Построение всех винтовых линий однотипно.
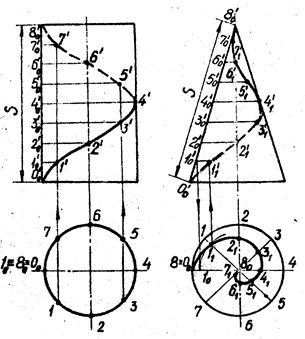
Рис. 10 а) б)
Список используемой литературы.
1. Анисимов И. К. Конспекты лекций по начертательной геометрии. – Р. 1970.
2. Фролов С. А. Начертательная геометрия: учебник для вузов. – М.: Машиностроение, 1983.
Похожие работы
... закону. Эту линию называют образующей. Она может быть прямой, и тогда образованную ею поверхность относят к классу линейчатых. Если образующая - кривая линия, поверхность считают нелинейчатой. Линию, по которой перемещают образующую, называют направляющей. В качестве последней иногда используют след поверхности, т. е. линию ее пересечения с плоскостью проекций. Определителем поверхности называют ...
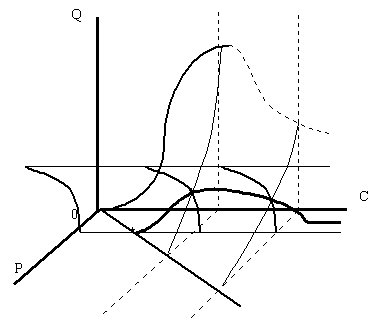
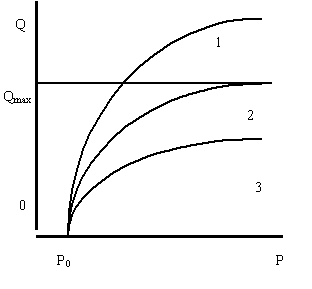
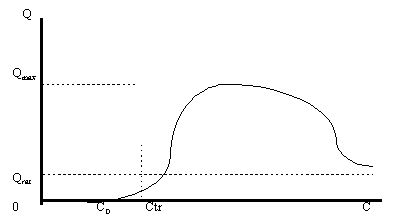
... и увеличить объемы потребления до максимально возможных значений и платить при этом все возрастающую с ростом дохода цену. Равновесные кривые для товаров, не являющихся предметами повседневного спроса Случаи равновесных кривых для товара повседневного спроса определяются месторасположением линии максимальных объемов поверхности спроса и поверхности предложения. Для товаров, которые не являются ...
... поверхности, которые в пересечении с данными поверхностями дают простые для построения линии (например, прямые или окружности). В общем случае вспомогательные секущие плоскости применяют и для построения линии пересечения кривой поверхности гранной. Изложенный общий способ построения линии пересечения одной поверхности другою не исключает применения другого способа, если хотя бы одна из этих ...
... , повысить интерес к учению; 3) углубить знания, полученные на уроках математики. Ход занятия I. Организационный момент II. Основная часть 1) Лекция об истории изучения плоских кривых [см. гл. I § 1] 2) Задание Ребята, разгадаем с вами кроссворд: ПАСКАЛЬ ПАПИРУС АПОЛЛОНИЙ РОБЕРВАЛЬ АРХИМЕД ГЕОМЕТРИЯ По горизонтали 1. Учёный, считавший, что дуга спирали ...
0 комментариев