Навигация
2. ОБУЧЕНИЕ ЧЕРЕЗ ЗАДАЧИ
Метод обучения математике через задачи базируется на следующих дидактических положениях:
1) Наилучший способ обучения учащихся, дающий им сознательные и прочные знания и обеспечивающий одновременное их умственное развитие, заключается в том, что перед учащимися ставятся последовательно одна за другой посильные теоретические и практические задачи, решение которых дает им новые знания.
2) Обучение на немногочисленных, но хорошо подобранных задачах, решаемых школьниками в основном самостоятельно, способствует вовлечению их в творческую исследовательскую работу, последовательно проводя через этапы научного поиска, развивает логическое мышление.
3) С помощью задач, последовательно связанных друг с другом, можно ознакомить учеников даже с довольно сложными математическими теориями.
4) Усвоение материала курса через последовательное решение учебных задач происходит в едином процессе приобретения новых знаний и их немедленного применения, что способствует развитию познавательной самостоятельности и творческой активности учащихся.
Можно выделить следующие виды обучения через задачи на внеурочных занятиях.
Теоретический материал изучаемого математического курса раскрывается конкретно-индуктивным путем. Учащиеся, решая самостоятельно подготовительные задачи, анализируя, сравнивая и обобщая результаты решений, делают индуктивные выводы. Способы решения конкретных задач таковы, что их можно применить при решении обобщенной задачи (теоремы), тем самым ученики готовятся к дедуктивным доказательствам, которые они в дальнейшем могут осуществить самостоятельно при выполнении нестандартных упражнений на применение теории и решение задач повышенной трудности.
Весь материал курса раскрывается через задачи в основном дедуктивным путем. Теоремы курса имеют вид задач. Полученные знания находят применение при решении творческих исследовательских задач.
Материал курса раскрывается через задачи комбинированным путем, т. е. как конкретно-индуктивным, так и дедуктивным. В курсе содержатся подготовительные, основные и вспомогательные задачи. Для индивидуальных заданий предусмотрены задачи повышенной трудности и творческие, исследовательские задачи.
Рассмотрим более подробно каждый из этих видов обучения.
Подготовительные задачи чаще всего располагаются в серии с нарастающей трудностью. Схематически ее можно изобразить так: А1—А2—А3—...—Ап, где Аk (k=1, 2, 3, .... n) — подготовительная задача, решение которой способствует самостоятельному решению учеником задачи Ak+1.
Каждая подготовительная задача должна быть небольшой по объему информации, доступной для самостоятельного решения учащимися. Особенно важно это для первых задач серии, так как успех в решении одной задачи стимулирует самостоятельную деятельность школьника при решении следующей. Задачи подбираются средней трудности, чтобы быть доступными всем ученикам. Если взять слишком легкие задачи, то у сильных учащихся пропадает интерес к их решению. Слишком же трудные задачи исключают самостоятельность решения для всех учащихся. При возникновении затруднений учителем должна быть оказана индивидуальная помощь.
В ходе решения задач обязательно их письменное оформление, чтобы можно было, охватив решения всех задач серии, проследить пути к решению основной задачи-проблемы, сделать необходимые обобщения. Если первые задачи серии окажутся для какого-то ученика слишком легкими, он может по своему усмотрению начать письменное оформление решений с задачи Ak, т. е. с промежуточной задачи. Тогда для него подготовительная серия задач будет иметь вид Ak—Ak+1—...—An.
Решения задач обсуждаются коллективно, анализируются различные способы решения, проводится обобщение полученных результатов, формулируется учебная проблема и намечается способ ее решения. Всячески поощряется самостоятельность суждений, отстаивание учащимися собственного мнения. (Смотри приложение 2)
Идея использования вспомогательных задач возникла на основе наблюдений психологов о том, что при решении сложной задачи учащиеся обычно ищут, под какой из уже известных типов задач можно было бы ее подвести. При этом они, анализируя условие задачи, осуществляя поисковые пробы, пытались воспользоваться такими данными, которые способствовали бы переносу уже имеющегося в их опыте (полученном при решении ранее встречающихся задач) общего или частного метода, способа или приема решения задач. То есть способы решения одной задачи оказывают существенное влияние на самостоятельные поиски решения другой.
Вспомогательные задачи являются своеобразными указаниями к самостоятельной деятельности ученика при решении основной задачи. Они отличаются от указаний и готовых решений, имеющихся в большинстве пособий по математике для самостоятельной подготовки к конкурсным экзаменам, тем, что не содержат рецептов, не навязывают способ решения автора, не дают готового решения. Указание (подсказка) во вспомогательной задаче заключается в ее решении: нужно сначала самостоятельно решить вспомогательную задачу, а затем обнаружить содержащуюся в ней подсказку. Обычно для ученика одной вспомогательной задачи оказывается недостаточно. Тогда дается вторая вспомогательная задача и т. п. Образуется серия вспомогательных задач.
Схематично основная задача А вместе с серией вспомогательных задач A1, A2, ..., An изображается так: А: A1 —A2 —... —An.
Самостоятельная деятельность ученика начинается с решения задачи А. Если он за определенное время не сможет решить ее, то приступает к решению первой вспомогательной задачи А1: А—А1. В случае решения задачи А1 ученик снова возвращается к задаче А: А1—А. Если задача А снова не решается, то он обращается к задаче А2. Решив задачу A2, возвращается к задаче A и т. д. Возможен случай, когда школьник не сможет решить вспомогательную задачу А1. Тогда он приступает к решению задачи А2. Если и A2 не решается, то переходит к задаче A3 и так до An. От задачи Anученик последовательно возвращается к задаче
А: An —An-1 —... —A1—A. Возможна и другая последовательность решения задач, что можно изобразить схемами:
A—A1 —A—A2 —A—A3 —A или
A—A1 —A—A2 —A1 —A—A3 —A2 —A1—A и т. д.
Составление вспомогательных задач наталкивается на серьезные трудности. Для решения задачи Л может соответствовать и другая серия вспомогательных задач, отличная от указанной, например В1, В2, ..., BkТрудность заключается в отборе лучшей (оптимальной) серии для конкретного ученика. Далее, серия может быть и нелинейна. Это получается тогда, когда для решения задачи A нужно знать способы решения сразу двух (или нескольких) задач. Схематическое изображение этой ситуации таково:
A: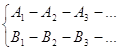
Трудность заключается в том, что одна и та же серия вспомогательных задач для разных учащихся имеет различную эффективность: для одних серия слишком длинна (содержит много задач), для других коротка, одни и те же задачи для одних слишком легки, для других трудны и т. п. Кроме того, вспомогательные задачи навязывают ученику определенный путь решения. Но и при подсказке учителя также навязывается ученику способ решения, намеченный учителем.
Опыт применения вспомогательных задач на кружковых и факультативных занятиях по математике показывает, что школьники, научившись самостоятельно решать задачи с помощью вспомогательных задач, предложенных учителем, замечают, что среди задач A1 —A2 —... —An имеются и такие, которые либо уже были решены ими ранее, либо решаются способами (приемами), известными им. Это наталкивает учащихся на мысль, что при решении новой задачи следует самостоятельно отыскивать среди уже решенных ранее задач родственные данной и использовать их в качестве вспомогательных. Так воспитывается умение при самостоятельном решении задач возвращаться к своему опыту и применять его при продвижении вперед. Последнее является важным звеном умения решать задачи, умения самостоятельно приобретать новые знания.
Курсы, построенные на задачах, не содержат деления материала на теоретическую и практическую части. Сами задачи — это и есть изучаемый курс. Поэтому и содержание задач, и способы решения их направлены как на вооружение учащихся теоретическими знаниями, так и на выработку умений и закрепление навыков. Рассматриваемые определения обычно включаются в содержание задач. Возможна формулировка определений и отдельно от задач. Теоремы имеют тоже вид задач. Если теорема большая или сложная, то она разбивается на последовательность таких задач, что решение предыдущей облегчает решение последующей, а совокупность этих решений дает доказательство теоремы.
Любая тема курса состоит из серии задач, которые должны быть полностью решены каждым учеником, так как только в этом случае достигается полное усвоение определенной математической теории. Однако в индивидуальные задания могут быть включены задачи подготовительные, вспомогательные или задачи для самоконтроля, которые не обязательны для всех учеников.
Перед изучением темы организуется пропедевтическая работа, ставящая своей целью подготовить учеников к самостоятельному активному изучению материала. В частности, здесь выявляются и ликвидируются пробелы в знаниях и формируются необходимые предварительные представления. Затем учитель в форме лекции или беседы вводит учеников в тему, намечает круг вопросов, подлежащих изучению, формулирует сам или подводит учащихся к самостоятельной формулировке первой проблемной задачи курса.
Основным этапом занятий является самостоятельное решение школьниками задач. Учащимся в процессе самостоятельной работы разрешается пользоваться справочниками и конспектами, поскольку необходимо умственное развитие, умение самостоятельно решить возникающие задачи. Индивидуальная помощь учителя носит характер не подсказки, а направления на верный путь решения, для чего используются вспомогательные задачи. Расположение задач в серии по принципу нарастающей трудности стимулирует развитие самостоятельности учеников. Обучение с использованием серии вспомогательных задач строится по принципу от сложного к простому, от трудного к более легкому, что способствует формированию элементов творчества, стимулирует поиски учащимися способов решения, побуждает их мыслить. После решения всех задач серии проводится коллективное обсуждение результатов. Полученный материал обобщается для последующего применения полученных знаний при решении нового класса задач, делаются теоретические выводы. Всячески поощряется самостоятельность учеников в суждениях, в отстаивании собственного мнения.
Как показал опыт, обучение через задачи на внеурочных занятиях обеспечивает развитие самостоятельности и творческой активности учащихся, способствует приобретению прочных и осознанных знаний, развивает умение сравнивать, обобщать, делать творческие выводы из решенных задач, поддерживает интерес к математике.
Похожие работы
... Оно и определило формулировку проблемы: каковы условия продуктивного формирования УД младших школьников при обучении математике с применением персональных компьютеров? Целью исследования является выявление особенностей формирования учебной деятельности младших школьников при обучении математике с применением ПК. Объектом исследования выступает методическая система обучения младших школьников ...
... росту. Существует определенная взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике. Глава II Развитие познавательного интереса к урокам математики младших школьников средствами использования занимательных дидактических игр 2.1 Дидактические игры, их виды В отличие от других видов деятельности игра содержит цель в самой себе; ...
... , умения и навыки; - наличие сильных учеников как группы позволяет постоянно продумывать работу с ними, учитывать возможности их развития. 3. Капиносов А.Н. в статье “Уровневая дифференциация при обучении математике в V-IX классах” [14] рассматривает разбиение учащихся на 4 группы. Основой разбиения являются различия учащихся в темпах овладения учебным материалом, а также в способностях ...
... моделей к текстовым задачам. Для этого необходимо в первую очередь изучить понятие текстовой задачи и рассмотреть виды вспомогательных моделей текстовых задач. Глава 2. Обучение построению вспомогательных моделей в процессе решения текстовых задач. 2. 1. Использование вспомогательных моделей в процессе решения текстовых задач. Решение любой ...
0 комментариев