Даны точки А(3;0), B(3,5), С(-1;3), К(-1;0). Вычис­лите площадь четырехугольника АBСK

1. Даны точки А(3;0), B(3,5), С(-1;3), К(-1;0). Вычис­лите площадь четырехугольника АBСK.

2. Даны точки А (2; 0), В (2; 3), С (- 1, 4), К (-3; 2). Е (-3; 0). Вычислите площади многоугольников АВСКЕ и ВСК.

3. Даны точки A (x₁; 0), В (х₂; 0), С (х₂; y₂), К (x₃; y₃), Е (x₁; y₁). Укажите способ вычисления площади треугольника СКЕ, если:

1) x₁<x₃<x₂, 0<y₂<y_l<y₃;

2) x₁<x₂<x₃, 0<y₃<y_l<y₂.

4. Даны точки A(x₁;y₁), В (х₂; у₂), C(х₃; у₃), где y₁, у₂, у₃ — положительные числа. Докажите, что площадь треугольника ABC может быть вычислена по формуле S=0.5|S₁|, где

S₁ =x₁ (y₂—y₃)+x₂ (у₃—y₁)+x₃ (у₁—y₂).

5. Докажите, что можно подобрать такой параллельный пе­ренос на вектор  (0; m), при котором точки A (х₁;у₁), В (х₂; y₂), С(х₃; у₃) перейдут в точки A' (х₁'; у₁'), B' (х₂'; у₂'), С' (х₃'; у₃'), причем у₁'>0, у₂'>0, у₃'>0.

6. Даны три точки А(х₁; у₁), В(х₂; у₂), С (х₃; у₃) и точки A' (х₁; у₁ +m), В'(х₂; у₂ +m), С' (х₃; у₃ +m), полученные при па­раллельном переносе на вектор (0; m), причем у₁ +m, у₂ +m, у₃ +m - положительны. Вычислите площадь треугольника А'В'С'. Объясните, почему результат не зависит от m.

7. Докажите, что площадь треугольника АВС вычисляется по формуле

S =0.5|x₁(y₂—y₃) + x₂ (у₃—y₁) + x₃ (у₁—y₂)|

независимо от того, какая из его вершин обозначена через (x₁;y₁), (х₂; у₂), (х₃; у₃),

Приложение 3

Заморочки из бочки

На столе ведущего стоит бочонок. Команды пооче­редно тянут из бочонка листочки с вопросами. На от­вет дается не более одной минуты.

Если бы завтрашний день был вчерашним, то до воскресенья осталось бы столько дней, сколько дней прошло от воскресенья до вчерашнего дня. Какой же сегодня день? [Среда.]

Груша тяжелее, чем яблоко, а яблоко тяжелее перси­ка. Что тяжелее — груша или персик? [Груша.]

Два мальчика играли на гитарах, а один на балалай­ке. На чем играл Юра, если Миша с Петей и Петя с Юрой играли на разных инструментах? [Юра играл на гитаре.]

На столе стояли три стакана с ягодами. Вова съел один стакан и поставил его на стол. Сколько стаканов на столе? [Три.]

Шел муж с женой, да брат с сестрой. Несли 3 яблока и разделили поровну. Сколько было людей? [Трое: муж, жена и брат жены.]

У Марины было целое яблоко, две половинки и че­тыре четвертинки. Сколько было у нее яблок? [Три.]

Батон разрезали на три части. Сколько сделали раз­резов? [Два.]

Мальчик Пат и собачонка весят два пустых бочонка. Собачонка без мальчишки весит две больших коврижки. А с коврижкой поросенок весит — видите — бочонок. Сколько весит мальчик Пат? Сосчитай-ка поросят. [Мальчик весит столько же, сколько два поросенка.]

Один мальчик говорит другому: «Если ты дашь мне половину своих денег, я смогу купить карандаш». Сколько денег было у второго мальчика? [Установить невозможно.]

Петя и Миша имеют фамилии Белов и Чернов. Ка­кую фамилию имеет каждый из ребят, если Петя на год старше Белова. [Петя Чернов и Миша Белов.]

Человек, стоявший в очереди перед Вами, был выше человека, стоявшего после того человека, который стал перед Вами. Был ли человек, стоявший перед вами выше Вас? [Да.]

Как в древние времена называли «ноль»? [Цифра.]

Может ли при сложении двух чисел получиться нуль, если хотя бы одно из чисел не равно нулю? [Нет, не может.]

В каком случае сумма двух чисел равна первому сла­гаемому? [Когда второе слагаемое — нуль.]

Который сейчас час, если оставшаяся часть суток вдвое больше прошедшей? [8 часов.]

В семье я рос один на свете,

 И это правда, до конца.

Но сын того, кто на портрете,

Сын моего отца.

Кто изображен на портрете? [Мой отец.]

Игра «Счастливый случай»

Вопросы для первой команды

Отрезок, соединяющий точку окружности с ее цен­тром. [Радиус.]

Отрезок, соединяющий вершину треугольника с се­рединой противолежащей стороны. [Медиана.]

Два созвездия, по форме напоминающие ковш. [Большая Медведица и Малая Медведица.]

Аппарат для подводного плавания. [Акваланг.]

Утверждение, требующее доказательства. [Теорема.]

График квадратичной функции. [Парабола.]

Цифровая оценка успехов. [Балл.]

Множество точек плоскости, равноудаленных от конца данного отрезка. [Перпендикуляр, проведенный к середине данного отрезка.]

Угол, смежный с углом треугольника при данной вершине. [Внешний угол.]

Прямоугольник, у которого все стороны равны. [Квадрат.]

Мера веса драгоценных камней. [Карат.]

Часть круга, ограниченная дугой и ее хордой. [Сегмент.]

Направленный отрезок. [Вектор.]

Отношение противолежащего катета к гипотенузе. [Синус.]

Угол, меньший прямого. [Острый.]

Вопросы для второй команды

Отрезок, соединяющий любые две точки окружнос­ти. [Хорда.]

Утверждение, не вызывающее сомнений. [Аксиома.] Устройство для запуска двигателя внутреннего сго­рания. [Стартер.]

 Вид местности, открывающийся с возвышенного места. [Панорама.]

Самая знаменитая звезда в созвездии Малой Медве­дицы. [Полярная.]

График линейной функции. [Прямая.] Множество точек пространства, равноудаленных от данной точки. [Сфера.]

Кусок, часть чего-нибудь. [Осколок.] Сумма длин всех сторон многоугольника. [Пери­метр.]

Ромб, у которого все углы прямые. [Квадрат.] Зажим для присоединения, закрепления проводов. [Клемма.]

Самая большая хорда в круге. [Диаметр.] Простейшее геометрическое понятие. [Точка.] Часть прямой, ограниченная с одной стороны. [Луч.] Отношение прилежащего катета к гипотенузе. [Ко­синус.]

Игра «Счастливый случай»

Вопросы для первой команды

Результат сложения. [Сумма.]

Сколько цифр вы знаете? [Десять.]

Наименьшее трехзначное число. [100.]

Сотая часть числа. [Процент.]

Прибор для измерения углов. [Транспортир.]

Сколько сантиметров в метре? [Сто.]

Сколько секунд в минуте? [Шестьдесят.]

Результат деления. [Частное.]

Сколько лет в одном веке? [Сто.]

Наименьшее простое число. [2.]

Сколько нулей в записи числа миллион? [Шесть.]

Величина прямого угла. [90°.]

Когда произведение равно нулю? [Когда хотя бы один из множителей равен 0.]

График прямой пропорциональности. [Прямая, проходящая через начало координат.]

Что больше: 2 м или 201 см? [201 см.]

Что меньше:  или 0,5? []

Радиус окружности 6 см. Диаметр? [12 см.]

Какую часть часа составляют 20 мин? [1/3.]

Сколько сантиметров составляет 1% метра? [1см.]

 Корень уравнения |х| = —1. [Не существует.]

Вопросы для второй команды Результат вычитания. [Разность.]

 На какое число нельзя делить? [На 0.]

Наибольшее двузначное число. [99.]

Прибор для построения окружности. [Циркуль.]

Сколько граммов в килограмме? [Тысяча.]

Сколько минут в часе? [Шестьдесят.]

 Сколько часов в сутках? [Двадцать четыре.]

Результат умножения. [Произведение.]

Сколько дней в году? [365 или 366.1

Наименьшее натуральное число. [1.]

Сколько нулей в записи числа миллиард? [Девять.]

Величина развернутого угла. [180°.]

Когда частное равно нулю? [Когда делимое равно нулю.]

График обратной пропорциональности. [Гипербола.]

Что больше: 2 дм или 23 см? [23 см.]

4 Что меньше: 0,7 или  [0,7.]

Диаметр окружности 8 м. Радиус? [4 м.]

Какую часть минуты составляют 15 сек? [1/4.]

Найдите 10% тонны. [100 кг.]

Корень уравнения |х| = —7. [Не существует.]

Игра «Третий лишний»

Командам поочередно демонстрируются названия различных объектов. Два из них имеют какое-то общее свойство, а третий нет. Команды должны быстро отве­тить, какой объект не обладает свойством, которое присуще двум другим. Например:

гектар, сотка, метр;

ярд, тонна, центнер;

конус, квадрат, призма;

треугольник, прямоугольник, ромб;

прямая, отрезок, угол.

Игра «Что? Где? Когда?»

Вопросы

Индийцы называли его «сунья», арабские матема­тики «сифр». Как мы называем его сейчас? [Нуль.]

Именно этот учебник был первой в России энцик­лопедией математических знаний. По нему учился М.В.Ломоносов, называвший его «вратами учености». Именно в нем впервые на русском языке введены по­нятия «частное», «произведение», «делитель». Назо­вите учебник и его автора. [«Арифметика» Л.Ф.Маг­ницкого.]

Это название происходит от двух латинских слов «дважды» и «секу», буквально «рассекающая на две части». О чем идет речь? [О биссектрисе.]

Ее знакомство с математикой произошло в 8 лет, так как стены ее комнаты были оклеены листами с записями лекций по математике профессора Остроград­ского. Кто она? [С.В.Ковалевская.]

На могиле этого великого математика был установ­лен памятник с изображением шара и описанного око­ло него цилиндра. Почти спустя 200 лет по этому чертежу нашли его могилу. Кто этот математик? [Ар­химед.]

В древности такого термина не было. Его ввел в XVII в. французский математик Франсуа Виет, в переводе с латинского он означает «спица колеса». Что это? [Ра­диус.]

В черном ящике лежит предмет, название которого произошло от греческого слова, означающего в пере­воде «игральная кость». Термин ввели пифагорейцы, а используется этот предмет в играх маленькими детьми. Что в черном ящике? [Куб, кубик.]

Слово, которым обозначается эта фигура, в перево­де с греческого означает «натянутая тетива». Что это? [Гипотенуза.]

Точка, от которой в Венгрии отсчитывают расстоя­ния, отмечена особо. В этом месте в центре Будапешта стоит памятный знак. Кто или что было удостоено та­ких почестей? [Нуль.]

Воины римского консула Марцелла были надолго задержаны у стен города Сиракузы мощными машина­ми-катапультами. Их изобрел для защиты своего горо­да великий ученый Архимед. В черном ящике лежит еще одно изобретение Архимеда, которое и поныне используется в быту. Что в черном ящике? [Винт Ар­химеда, используется в мясорубке.]

Мы, в отличие от египтян, римлян и славян, пользу­емся позиционной системой счисления, в которой все­го десять цифр и «ступеньки». Что это за «ступеньки», перечислите их. [Это разряды, их всего три - едини­цы, десятки, сотни.]

Математическая пьеса «Бесплатный обед»

(по мотивам рассказа Я.И.Пврвльмана)

Ведущий. Десять друзей, решив отпраздновать окон­чание средней школы в ресторане, заспорили у стола о том, как усесться вокруг него.

Первый друг. Давайте сядем в алфавитном порядке, тогда никому не будет обидно.

Второй. Нет, сядем по возрасту.

Третий. Нет, нет. Сядем по успеваемости.

Четвертый. Да ну, опять успеваемость, это вам не школа, да и надоело.

Пятый. Тогда я предлагаю сесть по росту, и никаких проблем.

Шестой. Устроим здесь физкультуру не так ли?

Седьмой. Придется тащить жребий.

Восьмой. Ну уж нет.

Девятый. По-моему уже обед остыл.

Десятый. Я сажусь, где придется, и вы, давайте за мной.

Появляется официант. Вы еще не расселись? Моло­дые друзья мои, оставьте ваши пререкания. Сядьте за стол, как кому придется, и выслушайте меня.

Все сели как попало.

Официант. Пусть один из вас запишет, в каком по­рядке вы сейчас сидите. Завтра вы снова явитесь сюда пообедать и разместитесь уже в ином порядке. После­завтра сядете опять по-иному и т.д., пока не перепро­буете все возможные размещения. Когда же придет черед вновь сесть так, как сидите вы сегодня, тогда - обещаю торжественно — я начну ежедневно угощать вас всех бесплатно самыми изысканными обедами.

Друзья почти хором. Вот здорово, будем каждый день обедать у вас.

Друзья сидят за столом, выходит вперед ведущий.

Ведущий. Друзьям не пришлось дождаться того дня, когда они стали питаться бесплатно. И не потому, что официант не исполнил обещания, а потому что число всех возможных размещений за столом чересчур вели­ко. Оно равняется ни мало, ни много — 3 628 800. Такое число дней составляет, как нетрудно сосчитать, почти 10 000 лет! Вам может показаться невероятным, чтобы 10 человек могли размещаться таким большим числом различных способов. Проверьте расчет сами.

Возьмите любое трехзначное число. Допустим 475. Сколько еще можно получить чисел путем перестанов­ки цифр этого трехзначного числа?

Переставляя цифры, получим следующие числа: 475, 457, 745, 754, 547, 574. Всего 6 перестановок.

Добавим четвертую цифру: 4753. Сколько будет тогда перестановок?

4753, 4735, 4573, 4537, 4357, 4375, ...

Если каждую цифру поставить на первое место, то три другие дадут шесть перестановок, значит, так как у нас всего четыре цифры, то всего получится 4-6=24 перестановки. То есть, когда взяли три цифры, пере­становок получили 6, а когда взяли четыре цифры, перестановок оказалось 24. В первом случае число перестановок равно 1×2×3=6, во втором 1×2×3×4=24. А в нашей сценке число перестановок равно 1×2×3×4×5×6×7×8×9×10=3628800.

Математическая пьеса «Задача о чашах»

Много лет тому назад очень богатый шах объявил, что хочет разделить наследство между своими детьми, а того, кто поможет ему в этом, он щедро вознаградит.

Шах. В трех чашах хранил я жемчуг. Подарю я стар­шему сыну половину жемчужин из первой чаши, сред­нему — одну треть из второй, а младшему только чет­верть жемчужин из последней. Затем я подарю стар­шей дочери 4 лучшие жемчужины из первой чаши, средней — 6 жемчужин из второй чаши, а младшей дочери — две жемчужины из третьей чаши. И осталось у меня в первой чаше 38, во второй — 12, а в третьей — 19 жемчужин. Сколько жемчужин у меня должно быть в каждой чаше сначала? Хватит ли моего жемчуга для детей и меня?

Ведущий. И вот из разных стран пришли во дворец мудрецы. И первый мудрец, поклонившись шаху, на­писал свое решение задачи.

Первый мудрец. Если в первой чаше, о великий шах, останется 38 жемчужин, а подаришь ты старшей доче­ри 4 жемчужины, то эти 42 жемчужины и составят половину того, что хранится сейчас в чаше. Ведь вто­рую половину ты подаришь старшему сыну? Значит, в первой чаше у тебя должно быть сейчас 84 жемчужи­ны. Во второй чаше должно остаться 12 жемчужин, да 6 ты подаришь другой дочери. Эти 18 жемчужин со­ставят 2/3 того, что хранится во второй чаше сейчас. Ведь 1/3 ты пожалуешь среднему сыну. Значит, во второй чаше должно быть сейчас 27 жемчужин. Ну а в третьей чаше должно остаться 19 жемчужин, да две ты подаришь младшей дочери. Выходит, что 21 жемчу­жина - это 3/4 содержимого третьей чаши. Ведь 1/4 ты отдаешь младшему сыну. Значит, сейчас в третьей чаше должно быть 28 жемчужин.

Во время рассказа первый мудрец записывает реше­ние на доске:

38+4=42 42:1/2=42×2=84, 12+6=18 18:2/3=18-3/2=27, 19+2=21 21:3/4=21×4/3=28.

Шах. Как же ты смог решить такую сложную задачу?

Первый мудрец. Мне помогла арифметика — наука о числах, их свойствах и правилах вычисления. Это очень древняя наука, ей уже много тысяч лет.

Шах. Твое решение мне понятно, но оно длинное и утомило меня. А что скажет другой мудрец?

Второй мудрец. О великий шах! Я обозначу число жемчужин в первой чаше буквой х. Тогда старшему сыну ты подаришь  жемчужин. Если из х вычесть его половину, да еще 4 жемчужины, что ты подаришь старшей дочери, то остаток нужно приравнять к 38. Вот какое уравнение я составил:

x--4=38.

Решим его.  = 42, а х в два раза больше, т.е. х = 84. Выходит, что в первой чаше должно быть сейчас 84 жемчужины. А для второй чаши, если количество жемчу­жин в ней обозначить через у, получим уравнение

y--6=12

Решим его. у == 18, а теперь 18 разделим на 2 и умножим на 3. Значит у = 27.

Рассуждая также, составляем уравнение для третьей

чаши:

z--2=19, z =21, z =28.

Следовательно, в третьей чаше должно быть сейчас 28 жемчужин.

Шах. Твое решение мне тоже нравится. И ответы у вас одинаковые. Но нельзя ли решить это все как-то покороче?

Тогда молча вышел третий мудрец и показал плакат, где написано следующее:

х — ах — b = с.

Ответ: х= .

Шах. А здесь я ничего не понимаю! И вообще один ответ, а у меня три чаши!

Третий мудрец. Все три ответа уместились в одном, о великий шах! Ведь задачи про чаши совершенно одинаковые, лишь числа разные. Я и объединил три решения в одном, обозначив через х неизвестное число жемчу­жин, через а - часть жемчужин, подаренных сыну, че­рез b - число жемчужин, отданных дочери, а через с — число оставшихся в чаше жемчужин. Теперь можно под­ставлять вместо этих букв числа, которые ты задашь в своей задаче, и будут получаться правильные ответы. Будь у тебя 100 чаш, 100 сыновей, 100 дочерей, одного моего уравнения хватит, чтобы получить все ответы.

Шах. Да, твое решение, оказывается, самое удобное. Как же ты придумал его?

Третий мудрец. Мне помогла решить эту задачу алгеб­ра, как и второму мудрецу. В этой науке буквы исполь­зуются наравне с числами. Под буквой можно разуметь любое число. Алгебра дает самое короткое, самое общее решение для многих похожих друг на друга задач.

Игра «Аукцион»

На торги выносятся задания по какой-либо теме, причем учитель заранее договаривается с ребятами о теме игры. Пусть, например, это будет тема VIII клас­са «Действия с алгебраическими дробями».

В игре участвуют 4—5 команд. С помощью кодоскопа на экран проецируется лот № 1 — пять заданий на сокращение дробей. Первая команда выбирает задание и назначает ему цену от 1 до 5 баллов. Если цена этой команды выше тех, что дают другие, она получает это задание и выполняет его. Остальные задания долж­ны купить другие команды. Если задание решено вер­но, команде начисляются баллы — цена этого задания, если неверно, то эти баллы (или часть их) снимаются. Хочу обратить внимание на одно из достоинств этой простой игры: при выборе примера учащиеся сравни­вают все пять примеров и мысленно «прокручивают» в голове ход их решения.

Игра «Игрекс»

Эту игру можно проводить по любой теме на уроке или как внеклассное мероприятие. В классе или в ко­ридоре ставят столы, над которыми написаны плакаты:

фирма «Поиск», «Бюро добрых услуг», «Школбанк», магазин «Сладкоежка». Во всех фирмах работают стар­шеклассники. В игре может участвовать от 3 до 8 команд. Все команды зачисляются в фирму «Поиск» и получают одну или несколько задач первого уровня, причем каждая задача оценена в 500 игрексов (игреке — денежная единица, которую придумали ребята для этой игры). Решив задачи, команда сдает свою работу снова в фирму «Поиск». Руководители фирмы проверяют работы и оценивают их. На основании этих оценок банк выдает заработанные командой деньги. Банк также ведет размен денег и выдает кредит. Получив причита­ющееся число игрексов за задания первого уровня, команда приступает к задачам второго уровня и т.д. Если задача не получается, команда обращается за кон­сультацией в «Бюро добрых услуг», заплатив при этом 10% стоимости задачи. Выигрывает та команда, кото­рая заработает больше игрексов. В конце игры все команды покупают в магазине «Сладкоежка» на свои игрексы настоящие конфеты.

Приложение 4

Приведем примеры.

1. В IX классе на занятии математического кружка было предложено найти способ (путь) решения задачи: «Найти уравне­ние прямой, параллельной прямой у=2х—3 и проходящей через точку К(—3; 2).

Известная из аналитической геометрии формула у—у₀=k(х—х₀) учащимся не сообщалась. Они самостоятельно должны были отыскать путь решения предложенной задачи.

Решение.

Способ 1. Ученик предложил на прямой у=2х—3 рассмотреть любую точку, например А (0; —3). Затем в формулах параллель­ного переноса х'=х+а, у'=у+b подобрать параметры а и b так, чтобы точка A перешла в точку К. Это будет перенос: х'=х—3, у'=у+5. Прямую у=2х—3 подвергнем найденному параллель­ному переносу: x = x'+3; y = у'— 5;

у'— 5=2 (x'+ 3)—3; у'—5= 2x'+6—3; y'==2x'+8. После отбрасывания штрихов при пе­ременных получим ответ: y =2x+8.

Способ 2. Ученик предложил воспользоваться известным фактом, что в уравнениях параллельных прямых угловые коэф­фициенты равны. Поэтому искомое уравнение будет вида у=2х+b. Последнему удовлетворяют координаты точки K, по­этому 2=2×(-3)+b, b=8.

Ответ: y==2x+8.

2. В стенгазете математического кружка IX класса было предложено самостоятельно найти способы решения задачи: «Вы­числить расстояние от точки M (3; 2) до прямой Зх+4y+1=0».

Ученики нашли различные способы решения.

Способ 1. Воспользоваться готовой формулой, найденной учеником в учебнике по аналитической геометрии для втузов:

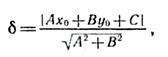
где Ах+Ву+С=0 — уравнение прямой, a x₀ и у₀ — координаты заданной точки.

Способ 2. На прямой Зх - 4y + 1 = 0 способом подбора найти две точки, например A (1; 1) и В (—3; —2). В треугольнике АВМ вычислить длины сторон и по формуле Герона площадь. Затем найти высоту, проведенную к стороне АВ. Это и будет искомое расстояние.

Способ 3. Найти уравнение прямой, проходящей через точку М перпендикулярно данной прямой. Затем вычислить координаты х₀ и у₀ точки пересечения этих прямых. Расстояние от точки (3; 2) до точки

(x₀; у₀) и будет искомым.

Приложение 5

 Приведем темы некоторых обзоров.

Тема 1. Координаты и задание фигур на плоскости (IX кл.).

Литература.

1) Гельфанд И. М., Глаголе­ва Е. Г., Кириллов А. А. Метод

координат.— М.: Наука, 1971.

2) Понтрягин Л. С. Знакомство с высшей математикой:

Метод координат.— М.: Наука, 1977.

Тема 2. Задачи на максимум и минимум (X кл.).

Литера т у р а.

1) Нагибин Ф. Ф. Экстремумы.— М.:

Просвещение, 1966.

2) Б е л я е в а Э. С., Монахов В. М. Экстремальные задачи.— М.:

Просвещение, 1977.

Тема 3. Применение математики при решении нематемати­ческих

задач (XI кл.).

Литература. 1) Маковецкий П. В. Смотри в ко­рень! — М.: Наука,

1984.

2) Попов Ю. П., Пухначев Ю.В. Математика в об­разах.— М.: Знание,

1989.

3) Тихонов А. Н., Костомаров Д. П. Рассказы о прикладной

математике.— М.: Наука, 1979.

Приложение 6

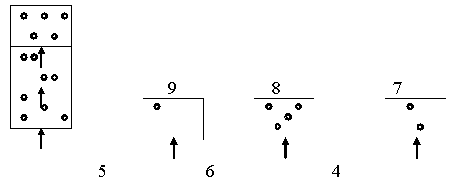
1. Между морскими портами А и В регулярно курсируют теплоходы одного и того же номерного рейса, отправляясь еже­дневно в полдень из одного порта и прибывая ровно в полдень через 7 суток в другой порт. Стоянка в порту — сутки. Сколько теплоходов своего рейса встретит команда одного из них на пути от Л до В? Каково наименьшее число теплоходов, необходимых для бесперебойного обеспечения расписания движений?

2. Найти геометрическое место середин всех хорд окружности, проходящих через заданную внутри ее точку.

3. Найти геометрическое место оснований перпендикуляров, опущенных из данной точки М на прямые, проходящие через точку К.

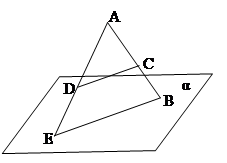
4. Механизм представляет собой равнобедренный треугольник СОК, в котором равные стороны ОС и ОК являются упругими (несжимаемыми и нерастяжимыми) стержнями, а сторона КС — резиновый (равномерно растяжимый) шнур. Какую линию опишет середина стороны КС, если сторону ОК оставить неподвижной, а сторону ОС вращать вокруг точки О?

Список литературы

1.   Под ред. Ю.К. Бабанского. Выбор методов обучения в средней школе. М., 1981.

2.   Бабанский Ю.К. Рациональная организация деятельности учащихся. М.: Знание 1981г. (Серия «Педагогика и психология»; №3 1981г.)

3.   Айзенберг М.И. Обучение учащихся методам самостоятельной работы. Математика в школе. 1982 №6.

4.   Кулько Б.А., Цехместрова Т.Д. Формирование у учащихся умений учиться: пособие для учителей. – М.: Просвещение, 1989 г.

5.   Минскин Е.М. От игры к знаниям. – М.: Просвещение, 1987 г.

6.   Сефибеков С.Р. Внеклассная работа по математике. – М.: Просвещение, 1988 г.

7.   Пичурин Л.Ф. Воспитание учащихся при обучении математике: книга для учителя. – М.: Просвещение, 1987 г.

8.   Самостоятельная деятельность учащихся при обучении математике (Формирование умений самостоятельной работы): Сборник статей, составитель Демидова С.И. – М.: Просвещение, 1990 г.

9.   Степанов В.Д. Внеурочная работа по математике в средней школе. – М.: Просвещение, 1991 г.

10.              Веселая математика. Журнал «Математика в школе №6, 1999 г.»