Навигация
АКТИВИЗАЦИЯ ВНЕКЛАССНОЙ РАБОТЫ
3. АКТИВИЗАЦИЯ ВНЕКЛАССНОЙ РАБОТЫ
Внеклассная работа по математике в ее традиционном толковании проводится в школе учителем во внеурочное время с учащимися, проявляющими к математике интерес. Эта работа планируется учителем и по мере необходимости корректируется. Государственных программ по внеклассной работе нет, как нет и норм оценок. На внеклассные мероприятия и занятия ученики приходят по желанию, без всякой предварительной записи. Если у ученика пропадет интерес к внеклассной работе, он прекращает свое участие в ней. Активизация внеклассной работы по математике призвана не только возбуждать и поддерживать у учеников интерес к математике, но и желание заниматься ею дополнительно как под руководством учителя во внеурочное время, так и при целенаправленной самостоятельной познавательной деятельности по приобретению новых знаний, т. е. путем самообучения.
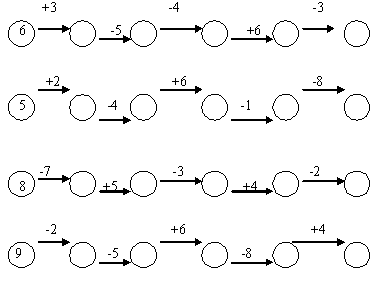
Одной из форм внеурочной работы являются конкурсы, которые обладают большим эмоциональным воздействием на участников и зрителей. (Смотри приложение 3)
4. ОРГАНИЗАЦИЯ САМООБУЧЕНИЯ ШКОЛЬНИКОВ С УЧЕТОМ ИНДИВИДУАЛЬНЫХ ИНТЕРЕСОВ И ПОТРЕБНОСТЕЙ
В дидактике установлено, что самостоятельная деятельность учащихся по приобретению новых знаний по собственной инициативе, сверх программы школьного предмета, возможна лишь при наличии серьезного интереса к предмету, увлечения рассматриваемыми проблемами, переходящего в познавательную потребность приобретать сверхпрограммные знания в соответствии с индивидуальными интересами и потребностями.
С помощью анкет, в ходе личных бесед можно установить, почему тот или иной ученик посещает занятия кружка или факультатива. В младшем возрасте, как правило, это интерес к математике как любимому учебному предмету, в среднем и старшем — это либо интерес к математике как науке, либо профессионально-ориентационный, связанный с предполагаемой послешкольной деятельностью. Например, в одной из школ с помощью анкет учитель установил, что среди семиклассников, регулярно занимающихся в математических кружках и факультативах, около 70% считают занятия по математике более любимыми в школе, чем по другим предметам, примерно 20% заявили о своем серьезном увлечении математикой как наукой и намерении посвятить математике свою трудовую послешкольную деятельность, а около 10% назвали другие причины, в том числе следование за товарищем, увлеченным математикой. Через два года анкетирование среди этих же учеников показало, что лишь 6% изъявляют желание глубоко изучать математику, 83% связывают дополнительные занятия математикой с необходимостью хорошо подготовиться к конкурсному экзамену по математике на вступительных экзаменах в вуз, а 11 % указывают другие причины. Для учителя полученные данные нужны для эффективного применения индивидуального подхода к школьникам во внеурочной работе, корректировки своей работы, направленной на развитие интереса учащихся в ходе внеурочных занятий. В противном случае первоначальный интерес к математике, не получая подкрепления и развития, гаснет и ученики прекращают посещать внеурочные мероприятия. Более того, они перестают самостоятельно заниматься математикой дома, фактически прекращают самообучение.
Интерес к математике формируется с помощью не только математических игр и занимательных задач, рассмотрения софизмов, разгадывания головоломок и т. п., хотя и они необходимы, но и логической занимательностью самого математического материала: проблемным изложением, постановкой гипотез, рассмотрением различных путей решения проблемной ситуации, решением задач или доказательством теорем различными методами и другими разработанными в методике математики приемами формирования познавательного интереса к математике. (Смотри приложение 4).
Разбор предложенных способов проходил на расширенном заседании математического кружка с привлечением учащихся из группы факультатива и приглашением желающих и вызвал неподдельный интерес у присутствующих. Необходимые вычисления проводились с помощью микрокалькулятора.
Самообучение школьника невозможно без его умения и желания работать с математической книгой.
Подбору математической литературы для самообучения учителю приходится уделять большое внимание. Установлено, что учащиеся по-разному работают над книгой: одни стараются побыстрее пройти теоретический материал и приступить к решению задач, другие больше внимания уделяют, наоборот, теоретическим вопросам. Первым не нравятся многословные учебники и пособия, они предпочитают краткие дедуктивные доказательства; вторые предпочитают книги с подробными выкладками, пояснениями, индуктивными выводами, примерами и т. п.
Так, в одной из школ на факультативных занятиях в старших классах изучение программирования на ЭВМ осуществлялось с помощью программированных пособий. На факультативе их применение оправдывалось тем, что ученикам предлагалось усваивать материал в индивидуальном темпе, затруднения преодолевались с помощью индивидуальных консультаций, а подведение итогов проводилось на заключительной конференции по книгам.
Наблюдения показали, что одни ученики старались быстрее овладеть теорией. Если оказывалось, что выбранный ими ответ неверен, то, не пытаясь разобраться в причинах ошибки, они искали другой ответ, пока не находили верный, позволявший им читать очередную запрограммированную порцию учебной информации. В процессе изучения материала пособия многие из этих учащихся составляли свой шифр — последовательность страниц для чтения с правильными ответами, а затем вторично прочитывали эти страницы в указанной шифром последовательности, т. е. читали как обычную книгу, а не как программированное пособие, составленное по разветвленной программе. Другим, наоборот, нравилось разбирать все замечания автора. Даже убедившись, что выбранный ими ответ верен, они читали указания и к другим, неверным ответам, чтобы рассмотреть приводимые примеры и уяснить причины возможных неправильных ответов.
При переходе в дальнейшем к изучению обычной литературы по программированию на ЭВМ первые испытывали чувство удовлетворения от того, что их не перебивают то и дело вопросами, на которые нужно давать ответ, а в случае неверного выбора еще и перечитывать назидания автора. вторые же не всегда удовлетворялись краткостью авторского изложения материала, постоянно обращались к учителю с вопросами, чувствуя необходимость в его комментариях.
С учетом избирательного отношения учеников к математическим книгам можно рекомендовать для самообучения не одно учебное пособие, а несколько, чтобы ученики сами выбирали то, которое им больше подходит по их индивидуальным склонностям и способностям. Правда, учителю в этом случае труднее контролировать их самостоятельную работу над книгой и проводить консультации. Зато самообучение школьников будет более эффективным.
Большое значение для стимулирования самообучения имеет организация обзоров изученной учащимися математической литературы, ее обсуждение на читательских конференциях или в устных журналах. Обычно делается это так. Объявляется тема для обзора и рекомендуется литература. Список литературы помещается на стенде. Там же указывается расписание консультаций. Дается время для подготовки, назначается место и время проведения.
Обзор литературы делают два-три ученика, они же отвечают на вопросы. Впрочем, отвечать могут и присутствующие ученики и учитель, а также дополнять или поправлять докладчиков. При этом возникают споры, выдвигаются гипотезы, находятся новые решения и т. д. (Смотри приложение 5).
Для самостоятельного обучения очень важно воспитать у учащихся потребность в самостоятельном поиске знаний и их приложении. Поэтому одной из задач является приобщение учеников к решению задач по своей инициативе, сверх школьной программы. Одним из средств является математическая олимпиада. Школьники убеждаются на собственном опыте, что, чем больше разнообразных задач они самостоятельно решают, тем значительнее их успехи не только в школьной, но и в районной олимпиаде. Это служит дополнительным стимулом к самообучению.
Одним из условий самообучения является умение ученика
планировать свою самостоятельную внеурочную познавательную деятельность по приобретению знаний. Учитель помогает ему в составлении индивидуальных планов самообучения и в их реализации. Если в V—VII классах самообучение школьника проводится обычно по плану, подсказанному учителем, в VIII—IX классах уже при совместных обсуждениях в индивидуальных или групповых беседах и консультациях, то в Х—XI классах эти планы составляются самим учеником. Лишь в некоторых случаях он прибегает к совету учителя или руководствуется его рекомендациями.
Так, в одной из групп факультатива XI класса учащимся было предложено уточнить свои индивидуальные планы самообучения на учебный год. В ходе индивидуальных бесед учитель установил, что ученики планировали изучение научной и научно-популярной математической литературы, посещение математического кружка школьников-старшеклассников при пединституте и математического лектория при политехническом институте, решение задач из сборников задач различных математических олимпиад (отечественных и зарубежных). Большое место в планах отводилось самостоятельной работе по подготовке к поступлению в вуз: изучению пособий по математике для поступающих в вуз и решению конкурсных задач, публикуемых в «Кванте», обучению на заочных подготовительных курсах в избранный или родственный вуз и т. д.
Выяснив планы учащихся, учитель осуществлял индивидуально-групповое педагогическое руководство самообучением школьников, которое проводилось в следующих направлениях:
— корректирование (уточнение, детализация) индивидуальных планов самообучения;
— подбор учебной, научно-популярной и научной литературы по математике для самостоятельного изучения;
— более конкретное ознакомление каждого учащегося с предполагаемой дальнейшей деятельностью и уточнение места и значения математических знаний в этой деятельности;
— проведение индивидуальных и групповых консультаций по вопросам самообучения;
— оказание практической помощи учащимся, готовящимся к поступлению в вузы, где от абитуриентов требуется более углубленная математическая подготовка (МГУ, МФТИ, МИФИ и другие институты).
Чтобы педагогическое руководство самообучением школьников было эффективным, целесообразно осуществлять определенную дифференциацию, которая по сути будет индивидуально-групповой. Это обусловлено тем, что учащихся по их познавательным интересам и практическим потребностям, которые они хотят удовлетворить, занимаясь самообразованием, можно разделить на условные группы.
К первой группе можно отнести учащихся с ярко выраженной
интеллектуальной потребностью в углубленном изучении математики, обусловленной стержневым познавательным интересом в области математики. Предполагаемая послешкольная деятельность их связана с серьезным изучением математики либо на математических факультетах университетов, либо в технических вузах с углубленным изучением математики.
Во вторую группу целесообразно включить учеников, основные познавательные интересы которых находятся в области физики, техники, в естественнонаучной или производственной сфере, а углубленное изучение математики вызывается потребностями послешкольной деятельности (например, обучением в технических вузах общеинженерных профилей, на естественных факультетах университетов, в техникумах и профтехучилищах по специальностям, связанным с электроникой, робототехникой и другой современной техникой).
Третью группу составляют школьники, познавательные интересы которых находятся в областях, не требующих углубленных математических знаний. Занятия математикой во внеурочное время у них обусловлено не потребностями в дальнейшей деятельности, а исключительно увлечением математикой, возникшим на уроках, любовью к математике как учебному предмету и сфере приложения интеллектуальных сил.
И наконец, в отдельную четвертую группу целесообразно объединить учащихся, познавательные интересы которых еще не сформировались, характер дальнейшей деятельности не определился, а внеурочные занятия математикой обусловлены различными, часто случайными мотивами.
Включение учеников в ту или иную группу учитель осуществляет по результатам индивидуальных бесед с учащимися и их родителями, а также с помощью анкетирования.
Контроль за самообучением школьников можно осуществлять различными способами. Наиболее эффективный — через конкурсы по решению задач и различные математические состязания, в том числе и межпредметного содержания. Конкурс желательно проводить в несколько заочных туров и заключительный очный. Решения задач участники конкурсов могут давать любые, но за каждый способ решения одной и той же задачи очки начисляются отдельно. Это поощряет поиски новых оригинальных путей решения задачи, использование теоретического материала из различных рекомендованных учителем по определенной теме математических книг.
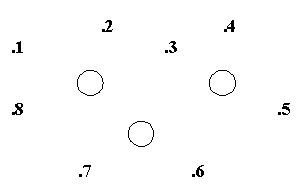
В качестве примера приведем задачи одного из туров заочного конкурса по решению задач в связи с самостоятельной работой школьников над темой «Метод координат». (Смотри приложение 6)
Условия задач помещаются на стенде. Там же указываются конкурсные требования, сроки сдачи письменных работ, место и время обсуждения представленных решений.
Об эффективности математического самообучения учитель может составить себе представление по многим критериям. Приведем некоторые из них:
а) повышение количества учащихся, изучающих дополнительную литературу;
б) смещение стержневого познавательного интереса школьников в сторону математики;
в) массовое применение в самостоятельных, контрольных и зачетных работах, при решении конкурсных и олимпиадных задач математических знаний, полученных в результате самообучения;
г) широкое участие в различных формах математического образования в системе внешкольного обучения: в заочной математической школе при АПН СССР и МГУ, на заочных подготовительных курсах для поступающих в вузы, в очных олимпиадах, проводимых на местах многими вузами (физтехом, МИФИ и др.), в воскресных математических лекториях при вузах и др.
Такая информация поможет учителю своевременно вносить коррективы в свою работу по организации самообучения учеников, способствовать повышению самостоятельности и творческой активности школьников для получения сверхпрограммных математических знаний в соответствии с их индивидуальными интересами, потребностями, планами дальнейшей деятельности.
ЗАКЛЮЧЕНИЕСпецифика внеурочных занятий состоит в том, что они проводятся по программам, выбранным учителем и обычно согласованным с учениками и корректируемым в процессе обучения с учетом их интеллектуальных возможностей, познавательных интересов и развивающихся потребностей. Участие в большинстве видов внеурочных занятий является необязательным, за результаты работы ученик отметок не получает, хотя его работа также оценивается, но другими способами: поощрениями через стенную печать, награждением грамотами, книгами, сувенирами и т. п.
Само участие ученика в факультативе, в кружковой работе, в математических состязаниях и олимпиадах уже является дифференциацией обучения в школе. Тем не менее и к этой категории школьников целесообразно для максимального развития их индивидуальных способностей и интересов, удовлетворения потребностей широко применять дифференциацию обучения на факультативных и кружковых занятиях и индивидуальный подход в организации и руководстве их самообучения.
Приложение 11. Учитель предлагает с помощью чертежей исследовать взаимное расположение гиперболы и прямой. Учащиеся выдвигают гипотезы (индуктивным путем). Затем после исследования системы уравнений
|
|
можно дать дедуктивное доказательство их (при |k| < |![]() | прямая пересекает гиперболу в двух точках, а при |k| ³ |
| прямая пересекает гиперболу в двух точках, а при |k| ³ |![]() | точек пересечения нет).
| точек пересечения нет).
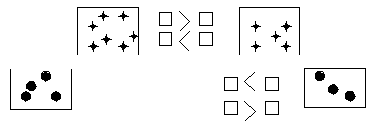
2. При изучении комплексных чисел ученикам предлагается исследовать возможные определения понятий «больше», «меньше» во множестве С. Затем на занятии в форме дискуссии опровергаются предлагаемые школьниками определения.
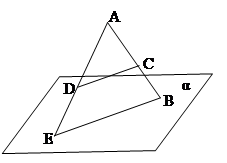
3. В качестве индивидуального задания рекомендуется исследовать возможное обобщение: точкам на прямой ставятся в соответствие действительные числа, точкам на плоскости — комплексные, а точкам в пространстве? Результатом исследования могут быть рефераты или сообщения учащихся, обсуждаемые коллективно на занятии.
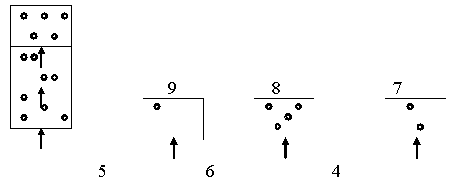
Приложение 2Приведем пример серии задач с нарастающей трудностью по теме «Площадь треугольника», в которой задачи 1—6 по сути являются подготовительными к задаче 7.
Похожие работы
... Оно и определило формулировку проблемы: каковы условия продуктивного формирования УД младших школьников при обучении математике с применением персональных компьютеров? Целью исследования является выявление особенностей формирования учебной деятельности младших школьников при обучении математике с применением ПК. Объектом исследования выступает методическая система обучения младших школьников ...
... росту. Существует определенная взаимосвязь проблем воспитания познавательного интереса и развития мышления в процессе обучения математике. Глава II Развитие познавательного интереса к урокам математики младших школьников средствами использования занимательных дидактических игр 2.1 Дидактические игры, их виды В отличие от других видов деятельности игра содержит цель в самой себе; ...
... , умения и навыки; - наличие сильных учеников как группы позволяет постоянно продумывать работу с ними, учитывать возможности их развития. 3. Капиносов А.Н. в статье “Уровневая дифференциация при обучении математике в V-IX классах” [14] рассматривает разбиение учащихся на 4 группы. Основой разбиения являются различия учащихся в темпах овладения учебным материалом, а также в способностях ...
... моделей к текстовым задачам. Для этого необходимо в первую очередь изучить понятие текстовой задачи и рассмотреть виды вспомогательных моделей текстовых задач. Глава 2. Обучение построению вспомогательных моделей в процессе решения текстовых задач. 2. 1. Использование вспомогательных моделей в процессе решения текстовых задач. Решение любой ...
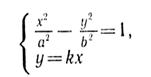
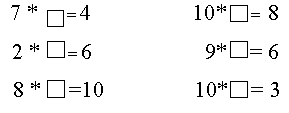
0 комментариев