Навигация
Устный опрос на обобщающем уроке
2.4. Устный опрос на обобщающем уроке
Хорошо подобранные системы устных упражнений способствуют формированию у учащихся умения обобщать. Для этого учащимся дается набор однородных упражнений, т. е. с одинаковой фабулой или одинаковыми логическими связями между входящими в них величинами. После рассмотрения каждой системы ученики на основании сопоставления реальных взаимосвязей, рассматриваемых в упражнениях, должны сделать вывод.
Урок алгебры в 8-м классе: "Решение квадратных уравнений"Цели урока: Обобщить и проконтролировать знания, умения и навыки учащихся, полученные при изучении темы “Решение квадратных уравнений”; развивать логическое мышление, тренировать память, развивать речь и умение комментировать; воспитывать интерес к предмету математики, умение общаться, прививать чувство товарищества и взаимопомощи.
Ход урока
I. Устный опрос.
– Какие уравнения называются квадратными?
– Прочитайте квадратное уравнение и назовите коэффициенты.
2х2 + 3х + 1 = 04m2 – 9 = 018 + 3x2 – x = 04t2 – 3t = 05y2 – 6y – 33 = 0- x2 – 5x = 01 – 25a2 = 05x2 = 9x + 2x2 – 1,3x = 0.7- y – 5 + 2y2 = 0x + 2x2 + 67 = 010p – 1 = 25p2
– Какие уравнения называются неполными квадратными уравнениями?
– Какие квадратные уравнения называются приведенными?
– Вы видите уравнения, сгруппированные по определённому признаку. Есть ли среди них лишние? Ответ объясните.
| 2x2 – x = 0 x2 – 16 = 02x2 = 0 4x2 – x – 3 = 0 | x2 – 9x + 20 = 0 9x2 – 6x +10 = 0 x2 + 3x – 5 = 0 2x2+ 2x + 1 = 0, 8 | 3x2 – 14x + 16 = 0 5x2 – 16x + 3 = 0 x2– x – 14 = 0 8 x2+ 10x – 25 = 0 |
(Предполагаемые ответы: в 1 столбце – лишнее 4-е уравнение, так как в первом столбце сгруппированы неполные квадратные уравнения; во 2-м столбце – лишнее 2-е уравнение, так как в этом столбце сгруппированы приведенные квадратные уравнения; в 3-м столбце – лишнее 3-е уравнение, так как в этом столбце сгруппированы уравнения с четным вторым коэффициентом).
(У доски работают три ученика, которые решают первые уравнения, каждый из своего столбца, а остальные продолжают устную работу.)
– Расскажите алгоритм полного квадратного уравнения.
– Что называется дискриминантом?
– Когда и сколько корней может иметь квадратное уравнение?
– Чему равны корни квадратного уравнения?
– Сформулируйте теорему Виета.
Урок алгебры в 9-м классе: "Уравнения"Цели урока: Обобщить и закрепить методы решения всех типов уравнений; способствовать выработке навыка решения уравнений; определить степень подготовленности учащихся по теме: «Уравнения» к контрольной работе.
Ход урока
I. Проверка домашнего задания.
Начинается урок с проверки домашнего задания, которое было дано по группам по разным уровням сложности. Заслушиваются сообщения выступающих, проверяются решения уравнений. Если встречаются ошибки, они учащимися исправляются. Проверка осуществляется с помощью кодоскопа: демонстрируются слайды с решениями уравнений из домашнего задания.
1 группа.
Линейные уравнения:
а) 2 - 3 (x + 2) = 5 - 2х;
x = -9.
б) ;
x = - 9.
2 группа.
Квадратные уравнения:
полные квадратные уравнения
6хІ - 7х +1= 0;
1=1; х2=.
неполные квадратные уравнения
а) в = 0, 25 -100 x= 0.
x = ; х2 = -.
б) с = 0, 3хІ - 12х = 0.
х1= 0 ; х2 = 4.
3 группа. Дробно–рациональные уравнения:.
6(2х+1) + 9(2х-1) = 12х2-15, если x = 0, то 4х2 -1 = 0-1, не равно 0.
= 0; = . если x =,то 4х2 -1 = 4* -1= 0.
ответ: 0
4 группа.
Алгебраические уравнения высших степеней:
Биквадратные уравнения
2х4 – 19х2 +9 = 0.
Пусть у =, тогда уравнение примет вид: 2у2 - 19у + 9=0.
=9; = .
Учитывая подстановку, имеем=, x= -, х3= , x= -.
Введение новой переменной
(х2 + 4х) (х2 + 4х - 17) + 60 = 0.
Пусть у = x+ 4х, тогда у (у-17) + 60 = 0, у1=12, у2=5.
Учитывая подстановку, имеем:
+ 4х = 12 и х2 + 4х = 5
х1= 2, х2 = -6 х3 =1, х4 = -5
Разложение левой части уравнения на множители
х3-2х 2-3х + 6 = 0.
(х-2)(х2-3)=0;
х1=2, х2 = - , х3 = .
II. Устная работа.
Задание: из ряда представленных уравнений, определите, к какому виду относится уравнение и каким способом его можно решить (уравнения выведены на экран через кодоскоп).
1..
2.6х4-3х 3+12х2- 6х = 0.
3..
4.(х-1)(5х + 0,5) = 0.
5.x(2х+1) = x + 4.
6.х6-7х3-8 = 0.
7. .
8. (х+1)2 - 0,81=0.
Тема:Обобщающий урок по теме «Квадратные уравнения»
Цель: Закрепить практические и теоретические знания и умения учащихся при выполнении заданий по теме «Квадратные уравнения»
Ход урока
Организационное начало урока
Сообщение темы и цели-Сегодня у нас особенный урок
-Мы проведем с вами «Звездный час» по теме «Квадратные уравнения», тем самым еще раз проверим свои знания и умения.
Закрепление материала
(Знакомство с правилами игры)
-Итак представим, что мы с вами в студии.
-Вы игроки, а я ведущая.
-У вас у каждого на партах лежат таблички с цифрами от 1 до 5.
| 1 | 2 | 3 | 4 | 5 | ||||||||||
-Итак, послушайте условия игры.
-Я буду задавать всем вопросы, а соответственно поднимать табличку с тем номером, который соответствует правильному ответу.
-А так же у каждого из вас лежат на партах листочки
-За каждый правильный ответ, когда я вам скажу вы будете на нем чертить звездочку.
-А в конце игры мы их подсчитаем и оценим работу каждого из вас.
Проведение игры
-Итак, начинаем игру
-Сейчас мы будем работать с вами по 1 табличке
Таблица №1
| 1 | 2 | 3 | 4 | 5 |
-Итак, сверху вы видите номера ответов
-А под ними соответствующие ответы
-Я задаю вопрос, вы 5 секунд думаете и поднимаете таблички с правильными ответами.
Какой вид имеет квадратное уравнение.
Назовите формулы корней квадратного уравнения.
Назовите неполное квадратное уравнение.
Назовите, чему равен дискриминант квадратного уравнения
-Хорошо с этим заданием вы справились хорошо, почти все учащиеся поднимали таблички с правильными ответами.
-А кто ошибался, он еще раз увидел правильные формулы и надеюсь так же доучит материал.
-А теперь мы все переходим во второй тур.
-Во втором туре мы выясним знание правил по данной теме.
Работать будем со второй табличкой.
Таблица №2
| 1 | 2 | 3 | 4 | 5 |
| Теорема обратная теореме Виета | Квадратное уравнение | Теорема Виета | Неполное квадратное уравнение | Приводимое квадратное уравнение |
Похожие работы
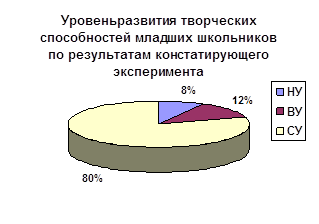
... в ходе исследования проводились различные занятия, игры, конкурсы для достижения цели эксперимента. Учащиеся сами составляли задания и выполняли проекты. Приведем примеры использования инновационных технологий в целях развития творческих способностей учащихся. Примеры заданий, составленных студентами в ходе выполнения проекте: Задание 1. Изучить устное народное творчество (пословицы) о труде и ...
... формирующего эксперимента, которая включала в себя создание и реализацию педагогических условий, выдвинутых нами первоначально в гипотезе. Развитие творческих способностей младших школьников на уроках окружающего мира по УМК начальной школы 21 века Н.Ф.Виноградовой будет осуществляться эффективнее при реализации следующих педагогических условий: 1). При реализации содержания текстов заданий ...
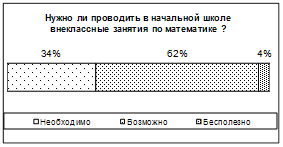
... и младших школьников. Анкета для студентов включала в себя два вопроса, один из которых о том, в чем, по их мнению, заключается развитие математических способностей школьников, а второй ¾ для выяснения отношения студентов к проведению внеклассной работы по математике в начальных классах. Анкета для преподавателей имела своей целью выяснить, проводят ли (а если проводят, то как часто) учителя ...
... . Самостоятельность в постановке и решении проблемы – существенные признаки творческой деятельности. Создание проблемных ситуаций на уроке закладывает основу для проблемных домашних заданий, направленных на развитие творческих способностей школьников, самостоятельное решение проблемы, поиск оптимальных путей, выводящих к конкретному результату. Большинство школьников говорят о таких заданиях, что ...

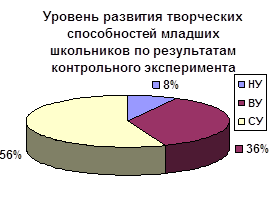
0 комментариев