АННОТАЦИЯ
В курсовом проекте решается задача вычисления площади произвольного многоугольника итерационным алгоритмом.
ЗАДАНИЕ.
Многоугольник (не обязательно выпуклый) задан на плоскости пересечением координат вершин в порядке обхода его границ. Определить площадь многоугольника.
СОДЕРЖАНИЕ
Аннотация
Задание на выполнение курсового проектаСодержание
Введение
1 Разработка программной реализации
2 Проверка на контрольных примерах
3 Заключение
Приложение 1. Блок-схема.
Приложение 2. Программа.
ВВЕДЕНИЕ
Системы, подобные представленной, часто можно встретить в повседневной жизни.
Данная задача не имеет аналитического решения. В геометрии существуют формулы, позволяющие вычислять площади правильных многоугольников, но для произвольных многоугольников таких формул нет. Решение задачи можно получить численными методами. Рассмотрим два из них.
1. Площадь произвольной фигуры можно вычислить методом Монте-Карло. Фигура вписывается в другую фигуру с известной площадью. Случайным образом на последнюю ставятся произвольное количество точек. Площадь определяется по формуле , где Nф – количество точек попавших в заданную фигуру, N – общее количество точек. Достоинство данного метода заключается в простоте реализации, сложность состоит только в определении попадания точки внутрь заданной фигуры. Очевидно, что точность вычисленной площади зависит от количества точек. Приемлемая точность может быть достигнута только при большом их количестве. В этом заключается один из недостатков метода. Точность также сильно зависит от качества генератора случайных чисел.
2. Из курса геометрии известно, что любой многоугольник можно разбить на несколько треугольников, соединяя отрезками несмежные вершины. Площадь многоугольника при этом будет равна сумме площадей полученных треугольников. В этом заключается второй метод определения площади. Площадь треугольника по заданным вершинам легко определяется по аналитическим формулам, поэтому этот метод позволяет получить большую точность при меньших затратах вычислительных ресурсов.
РАЗРАБОТКА ПРОГРАММНОЙ МОДЕЛИ.
Решение задачи будем производить, разбивая одну большую и трудную задачу на несколько небольших и несложных.
В черновом виде данный алгоритм можно представить в следующем виде:
1. Ввод вершин
2. Предварительная обработка
3. Пока количество вершин больше трех повторяем:
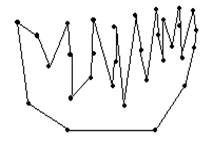
· Найти выпуклую вершин, т.е. вершину, внутренний угол которой меньше 1800. Например на рисунке вершины 1,3,4,5 являются выпуклыми.
· Отрезаем треугольник образованный этой вершиной и двумя смежными.
4. Площадь многоугольника будет равна сумме площадей отрезанных треугольников и площади оставшегося (при выходе из цикла) треугольника.
Рассмотрим все пункты алгоритма.
1) Ввод данных. Данные будем хранить в текстовом файле ,каждая первая строка которого содержит количество вершин, а последующие – пары координат (X,Y), разделенных пробелом. Координаты вершин и внутренние углы будем хранить в структуре типа:
sd: array[1..100] of
record
x,y: real;
angle: real;
end;
А количество вершин в глобальной переменной n.
Следующая процедура осуществляет ввод данных:
procedure input;
var f: text;
i: integer;
begin
Assign(f,'points.dat');
reset(f);
readln(f, n);
for i:=1 to n do readln(f, sd[i].x, sd[i].y);
end;
2) Предварительная обработка.
В данном пункте алгоритма осуществляется вычисление внутренних углов многоугольника.
Рассмотрим часть произвольного многоугольника:
Пусть вектор A образует с ось OX угол a1, а вектор B – угол a2. Тогда угол между ними (внутренний угол многоугольника) будет равен 180–a1–a2. Здесь нельзя использовать формулу угла между векторами через скалярное произведение, т.к таким образом вычисляется минимальный угол. Но при этом возможен такой случай:
Угол будет внешним.
Так вычислим либо все внутренние, либо все внешние углы многоугольника. Чтобы выяснить какие углы мы нашли, рассмотрим следующую теорему:
Сумма внешних углов произвольного многоугольника больше суммы внутренних.
Доказательство проведем по индукции:
1) Очевидно, что теорема справедлива для треугольника
2) Предположим, что теорема справедлива для k-угольника
3) Докажем теперь, что теорема справедлива для (k+1)-угольника.
Пусть сумма внутренних углов k-угольника равна a1, а внешних a2. Из п.2 следует, что a1<a2. k–угольник можно сделать (k+1)-угольником "нарастив" его на один треугольник:
Тогда сумма внутренних узлов (k+1)-угольника – a1+b+g+d, а внешних a2+(360-b)-g-d. Из геометрии известно, что сумма углов треугольника равна 1800. Тогда:
сумма внутренних углов: a1+180
сумма внешних углов: a2+360-(b+g+d)=a2+180.
Но из п.2 следует, что a1<a2. Следовательно, сумма внешних углов (k+1)-угольника больше суммы внутренних.(k+1)-угольника.
Теорема доказана.
Внутренние углы многоугольника будем вычислять следующим образом:
· для i-той вершины, имеющей координаты (Xi, Yi) найдем координаты входящих и выходящих векторов:
A{Xi–Xi–1, Yi–Yi–1} – входящий вектор
B{Xi+1–Xi, Yi+1–Yi} – выходящий вектор
· Вычисляем углы, образованные этими векторами с осями координат
· Вычисляем угол i-той вершины ji=180–a1–a2.
· Находим сумму
· Находим сумму
· Если S1<S2, то найденные углы являются внутренними, в противном случае внутренние углы равны 180-ji.
В языке Turbo Pascal нет функции Arccos(x), поэтому его вычисляем, используя следующую формулу . Но значение этой функции может изменяться в интервале от –900 до 900, поэтому при вычислении действительного угла будем учитывать квадрант, в котором лежит вектор.
Если в процессе отсечения углов произойдет ситуация, что три вершины подряд окажутся на одной прямой, то необходимо вторую из них удалить, т.к. она, строго говоря, не является вершиной и не будет влиять на дальнейшие вычисления. Для определения, лежит ли i-ая вершина на прямой, соединяющей (i–1)-ую и (i+1)-вершины, аналогично найдем входящий и выходящий вектора A и B. Затем их нормируем, т.е. делим каждую координату вектора на модуль этого вектора. Если после этого вектора окажутся равны, т.е. окажутся равными их координаты, то i-тую вершину можно удалить.
Учитывая все вышеприведенное, составляем процедуру вычисления внутренних углов.
procedure Angles;
var
al1,al2,
dx, dy, dxp, dyp,
s_in, s_out, a: real;
i,j: integer;
function ArcCos(a: real): real;
var res: real;
begin
if abs(a)<1.0E-30 then res:=pi/2
else res:=ArcTan(sqrt(1-a*a)/a);
if dx<0 then
if dy>=0 then res:=pi+res
else res:=-pi-res
else
if dy<0 then res:=-res;
ArcCos:=res
end;
begin
dxp:=sd[1].x-sd[n].x;
dyp:=sd[1].y-sd[n].y;
a:=sqrt(dxp*dxp+dyp*dyp);
dxp:=dxp/a;
dyp:=dyp/a;
i:=1;
while i<=(n-1) do
begin
dx:=sd[i+1].x-sd[i].x;
dy:=sd[i+1].y-sd[i].y;
a:=sqrt(dx*dx+dy*dy);
dx:=dx/a;
dy:=dy/a;
if (dx=dxp) and (dy=dyp) then
begin
dec(n);
for j:=i to n do sd[j]:=sd[j+1];
end;
dxp:=dx; dyp:=dy;
inc(i)
end;
dx:=sd[1].x-sd[n].x;
dy:=sd[1].y-sd[n].y;
al1:=ArcCos(dx/sqrt(dx*dx+dy*dy));
for i:=1 to n-1 do
begin
dx:=sd[i+1].x-sd[i].x;
dy:=sd[i+1].y-sd[i].y;
al2:=ArcCos(dx/sqrt(dx*dx+dy*dy));
sd[i].angle:=pi-al1+al2;
if sd[i].angle>2*pi then sd[i].angle:=sd[i].angle-2*pi
else
if sd[i].angle<0 then sd[i].angle:=2*pi+sd[i].angle;
al1:=al2
end;
dx:=sd[1].x-sd[n].x;
dy:=sd[1].y-sd[n].y;
al2:=ArcCos(dx/sqrt(dx*dx+dy*dy));
sd[n].angle:=pi-al1+al2;
if sd[n].angle>2*pi then sd[n].angle:=sd[n].angle-2*pi
else
if sd[n].angle<0 then sd[n].angle:=2*pi+sd[n].angle;
s_in:=0;
s_out:=0;
for i:=1 to n do
begin
if sd[i].angle<0 then sd[i].angle:=2*pi+sd[i].angle;
S_in:=S_in+sd[i].angle;
S_out:=S_out+(2*pi-sd[i].angle);
end;
if S_out<S_in then
for i:=1 to n do sd[i].angle:=2*pi-sd[i].angle;
end;
3) Нахождение выпуклых вершин.
Как было сказано выше, внутренний угол выпуклой вершины меньше 1800. Но не всякую выпуклую вершину можно "отрезать", т.к. линия "отреза" может пересекать стороны многоугольника. Например, вершину А "отрезать" нельзя:
Эта задача сводится к задаче о пересечении двух отрезков. Пусть отрезки заданы координатами своих концов. Первый отрезок A1(X1A, Y1A) и
A2(X2A, Y2A). Второй – B1(X1B, Y1B) и B2(X2B, Y2B).
1) Запишем уравнения прямой, проходящей через точки A1 и A2.
Преобразуем его в форму вида:
где , ,
Из геометрии известно, что если две точки находятся по одну сторону от прямой, то при подстановке их координат в полином левой части получим значения одного знака. Таким образом, если точки B1 и B2 располагаются по разные стороны от прямой, то
(AX1B+BY1B+C)(AX2B+BY2B+C)<0
Но пересечение прямых не является достаточным для пересечения отрезков, например:
Эти отрезки не пересекаются.
Для достаточного доказательства пересечения отрезков необходимо произвести все вышеприведенные операции над точками B1 и B2, т.е. провести через них прямую и выяснить расположение точек A1 и A2 относительно ее.
Таким образом определяем возможность отсечения вершины многоугольника с количеством вершин, больше четырех.
Для некоторых видов четырехугольника это условие не несправедливо, например:
Здесь вершину A отсечь нельзя. Для четырехугольника определяем расположение отсекаемой вершины и вершины, несмежной с ней (через оставшиеся проходит "линия отреза"). Если они расположены по одну сторону, как на рисунке, то отсекать нельзя. Приведенный алгоритм контроля реализуем в следующей функции:
function cross(c: integer): boolean;
var a, b, i: integer;
AA, BB, CC,
AA1, BB1, CC1: real;
function Mline(x,y: real): real;
begin
Mline:=AA*x+BB*y+CC
end;
function Sline(x,y: real): real;
begin
Sline:=AA1*x+BB1*y+CC1
end;
begin
if c=1 then
begin
a:=n;
b:=2;
end
else if c=n then
begin
a:=n-1;
b:=1;
end
else
begin
a:=c-1;
b:=c+1;
end;
cross:=true;
AA:=sd[b].y-sd[a].y;
BB:=-(sd[b].x-sd[a].x);
CC:=sd[a].y*(sd[b].x-sd[a].x)-sd[a].x*(sd[b].y-sd[a].y);
if n=4 then
begin
for i:=1 to n do
if (Mline(sd[i].x, sd[i].y)*Mline(sd[c].x, sd[c].y)>0) and (i<>c)
then exit;
cross:=false;
exit
end;
for i:=1 to n-1 do
begin
AA1:=sd[i+1].y-sd[i].y;
BB1:=-(sd[i+1].x-sd[i].x);
CC1:=sd[i].y*(sd[i+1].x-sd[i].x)-sd[i].x*(sd[i+1].y-sd[i].y);
if Mline(sd[i].x, sd[i].y)*Mline(sd[i+1].x,sd[i+1].y)<0 then
if Sline(sd[a].x, sd[a].y)*Sline(sd[b].x,sd[b].y)<0 then exit;
end;
AA1:=sd[1].y-sd[n].y;
BB1:=-(sd[1].x-sd[n].x);
CC1:=sd[n].y*(sd[1].x-sd[n].x)-sd[n].x*(sd[1].y-sd[n].y);
if Mline(sd[n].x, sd[n].y)*Mline(sd[1].x,sd[1].y)<0 then
if Sline(sd[a].x, sd[a].y)*Sline(sd[b].x,sd[b].y)<0 then exit;
cross:=false;
end;
4) Вычисление площадей отсеченных треугольников будем по формуле Герона
где .
function St(x1,y1, x2,y2, x3,y3: real): real;
var a, b, c, p: real;
begin
a:=sqrt(sqr(x1-x2)+sqr(y1-y2));
b:=sqrt(sqr(x1-x3)+sqr(y1-y3));
c:=sqrt(sqr(x3-x2)+sqr(y3-y2));
p:=(a+b+c)/2;
St:=sqrt(p*(p-a)*(p-b)*(p-c));
end;
5) Отсечение i-той вершины
dec(n);
for j:=i to n do sd[j]:=sd[j+1];
После отсечения какой-либо вершины необходимо заново рассчитать внутренние углы многоугольника, т.е. вызвать процедуру Angles.
После вычисления площади, выводим ее на экран и ожидаем нажатия любой клавиши.
Writeln('Площадь фигуры: ', S:3:3);
Readkey
Полный текст программы приведен в приложении 2.
Проверка на контрольных примерах.
Проверим работу программы на фигурах, площади которых можно вычислить по формулам.
1) Треугольник
Содержимое файла points.dat
3
0 0
5 0
2 3
Площадь треугольника по формуле:
Результат работы программы:
Площадь фигуры: 7.500
2) Прямоугольник
Содержимое файла points.dat
4
0 0
5 0
5 3
0 3
Площадь прямоугольника по формуле
Результат работы программы
Площадь фигуры: 15.000
3) Невыпуклая фигура
Содержимое файла points.dat
4
0 0
3 2
2 0
3 -2
Эта фигура симметрична относительно оси OX. Ее площадь будет равна
Результат работы программы:
Площадь фигуры: 4.000
Заключение.
Рассмотренный алгоритм является комбинацией аналитического и численного методов. Поэтому он включает в себя достоинства обоих. Т.к. основной операцией вычисления площади многоугольника является вычисление площади элементарного треугольника, то на результат вычисления не будут влиять методические погрешности, т.е. погрешности вносимые самим алгоритмом. Этим приведенный алгоритм отличается от метода Монте-Карло, точность которого зависит от количества точек. Погрешность будет вноситься лишь на этапе вычислений и будет определяться конкретной ЭВМ, на которой ведется расчет. Точность зависит от вещественного типа Real, в котором представляются основные переменные. Данный тип представим в компьютере лишь с определенной точностью, зависящей от внутреннего формата числа. Для персонального компьютера типа IBM PC/AT тип Real имеет следующие параметры:
· Длинна, байт................................. 6
· Количество значащих цифр......... 11…12
· Диапазон десятичного порядка... -39…+38
Эта точность вполне удовлетворительна для нашей задачи.
Приложение 1.
Блок-схема
Приложение 2. Текст программы.
Uses Crt;
const max=100;
var
n, i, j: integer;
sd: array[1..100] of
record
x,y: real;
angle: real;
end;
S: real;
procedure Angles;
var
al1,al2,
dx, dy, dxp, dyp,
s_in, s_out, a: real;
i,j: integer;
function ArcCos(a: real): real;
var res: real;
begin
if abs(a)<1.0E-30 then res:=pi/2
else res:=ArcTan(sqrt(1-a*a)/a);
if dx<0 then
if dy>=0 then res:=pi+res
else res:=-pi-res
else
if dy<0 then res:=-res;
ArcCos:=res
end;
begin
dxp:=sd[1].x-sd[n].x;
dyp:=sd[1].y-sd[n].y;
a:=sqrt(dxp*dxp+dyp*dyp);
dxp:=dxp/a;
dyp:=dyp/a;
i:=1;
while i<=(n-1) do
begin
dx:=sd[i+1].x-sd[i].x;
dy:=sd[i+1].y-sd[i].y;
a:=sqrt(dx*dx+dy*dy);
dx:=dx/a;
dy:=dy/a;
if (dx=dxp) and (dy=dyp) then
begin
dec(n);
for j:=i to n do sd[j]:=sd[j+1];
end;
dxp:=dx; dyp:=dy;
inc(i)
end;
dx:=sd[1].x-sd[n].x;
dy:=sd[1].y-sd[n].y;
al1:=ArcCos(dx/sqrt(dx*dx+dy*dy));
for i:=1 to n-1 do
begin
dx:=sd[i+1].x-sd[i].x;
dy:=sd[i+1].y-sd[i].y;
al2:=ArcCos(dx/sqrt(dx*dx+dy*dy));
sd[i].angle:=pi-al1+al2;
if sd[i].angle>2*pi then sd[i].angle:=sd[i].angle-2*pi
else
if sd[i].angle<0 then sd[i].angle:=2*pi+sd[i].angle;
al1:=al2
end;
dx:=sd[1].x-sd[n].x;
dy:=sd[1].y-sd[n].y;
al2:=ArcCos(dx/sqrt(dx*dx+dy*dy));
sd[n].angle:=pi-al1+al2;
if sd[n].angle>2*pi then sd[n].angle:=sd[n].angle-2*pi
else
if sd[n].angle<0 then sd[n].angle:=2*pi+sd[n].angle;
s_in:=0;
s_out:=0;
for i:=1 to n do
begin
if sd[i].angle<0 then sd[i].angle:=2*pi+sd[i].angle;
S_in:=S_in+sd[i].angle;
S_out:=S_out+(2*pi-sd[i].angle);
end;
if S_out<S_in then
for i:=1 to n do sd[i].angle:=2*pi-sd[i].angle;
end;
procedure input;
var f: text;
i: integer;
begin
Assign(f,'points.dat');
reset(f);
readln(f, n);
for i:=1 to n do readln(f, sd[i].x, sd[i].y);
end;
function St(x1,y1, x2,y2, x3,y3: real): real;
var a, b, c, p: real;
begin
a:=sqrt(sqr(x1-x2)+sqr(y1-y2));
b:=sqrt(sqr(x1-x3)+sqr(y1-y3));
c:=sqrt(sqr(x3-x2)+sqr(y3-y2));
p:=(a+b+c)/2;
St:=sqrt(p*(p-a)*(p-b)*(p-c));
end;
function cross(c: integer): boolean;
var a, b, i: integer;
AA, BB, CC,
AA1, BB1, CC1: real;
function Mline(x,y: real): real;
begin
Mline:=AA*x+BB*y+CC
end;
function Sline(x,y: real): real;
begin
Sline:=AA1*x+BB1*y+CC1
end;
begin
if c=1 then
begin
a:=n;
b:=2;
end
else if c=n then
begin
a:=n-1;
b:=1;
end
else
begin
a:=c-1;
b:=c+1;
end;
cross:=true;
AA:=sd[b].y-sd[a].y;
BB:=-(sd[b].x-sd[a].x);
CC:=sd[a].y*(sd[b].x-sd[a].x)-sd[a].x*(sd[b].y-sd[a].y);
if n=4 then
begin
for i:=1 to n do
if (Mline(sd[i].x, sd[i].y)*Mline(sd[c].x, sd[c].y)>0) and (i<>c) then exit;
cross:=false;
exit
end;
for i:=1 to n-1 do
begin
AA1:=sd[i+1].y-sd[i].y;
BB1:=-(sd[i+1].x-sd[i].x);
CC1:=sd[i].y*(sd[i+1].x-sd[i].x)-sd[i].x*(sd[i+1].y-sd[i].y);
if Mline(sd[i].x, sd[i].y)*Mline(sd[i+1].x,sd[i+1].y)<0 then
if Sline(sd[a].x, sd[a].y)*Sline(sd[b].x,sd[b].y)<0 then exit;
end;
AA1:=sd[1].y-sd[n].y;
BB1:=-(sd[1].x-sd[n].x);
CC1:=sd[n].y*(sd[1].x-sd[n].x)-sd[n].x*(sd[1].y-sd[n].y);
if Mline(sd[n].x, sd[n].y)*Mline(sd[1].x,sd[1].y)<0 then
if Sline(sd[a].x, sd[a].y)*Sline(sd[b].x,sd[b].y)<0 then exit;
cross:=false;
end;
begin
ClrScr;
input;
Angles;
S:=0;
while n>3 do
begin
i:=1;
while (sd[i].angle>pi) or (cross(i)) do
inc(i);
if i=1 then
S:=S+St(sd[1].x,sd[1].y, sd[2].x,sd[2].y, sd[n].x,sd[n].y)
else
if i=n then
S:=S+St(sd[n].x,sd[n].y, sd[1].x,sd[1].y, sd[n-1].x,sd[n-1].y)
else S:=S+St(sd[i].x,sd[i].y, sd[i-1].x,sd[i-1].y, sd[i+1].x,sd[i+1].y);
dec(n);
for j:=i to n do sd[j]:=sd[j+1];
Angles
end;
S:=S+St(sd[1].x,sd[1].y, sd[2].x,sd[2].y, sd[3].x,sd[3].y);
Writeln('Площадь фигуры: ', S:3:3);
Readkey
end.
Похожие работы
... должны стать все заданные точки. (См., например, [5], аналогичная задача предлагалась на кировской областной олимпиаде 2002г.). Решение. Следующий рисунок проиллюстрирует идею одного из возможных способов решения данной задачи: 2. Численное решение геометрических задач В ряде случаев при решении геометрических задач формулы из вычислительной геометрии могут оказаться слишком громоздкими ...
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...
... подобраны опорные задачи, которые можно использовать на уроке при изучении данной темы. Таким образом, в данной работе были рассмотрены основные, общие моменты изучения многогранников в школьном курсе стереометрии. В следствие чего дальнейшие исследования могут проходить в направлении более детального изучения отдельных разделов данной темы, а также пропедевтического введения многогранников в ...
... у Евклида и означает дословно “параллеле-плоскостное тело”. Греческое слово “кубос” употребляется Евклидом в том же смысле, что и наше слово “куб” 2.7. Параллелепипед Определение. Призма, основание которой - параллелограмм, называется параллелепипедом. В соответствии с определением параллелепипед - это четырехугольная призма, все грани которой - параллелограммы (рис. ). Параллелепипеды, как и ...




0 комментариев