Навигация
Реферат
по геометрии
на
тему:
“Призма”
учащейся
2 курса
Московского
Экстерната
Москва
1996
Оглавление
1. Краткий обзор развития геометрии 3
1.1 Общий исторический обзор 3
1.2. О развитии геометрии в Древней Греции до Евклида 6
2. Призма 11
2.1 Площадь поверхности призмы 13
2.2. Призма и пирамида 16
2.3. Пирамида и площадь ее поверхности 18
2.4. Измерение объемов 20
2.5. О пирамиде и ее объеме 21
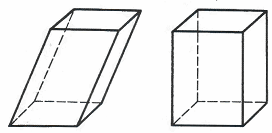
2.6. О призме и параллелепипеде 23
2.7. Параллелепипед 24
3. Симметрия в пространстве 29
Призма 30
Задачи 31
Литература 35
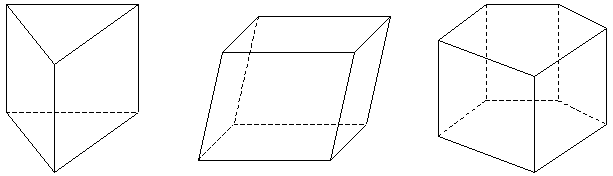
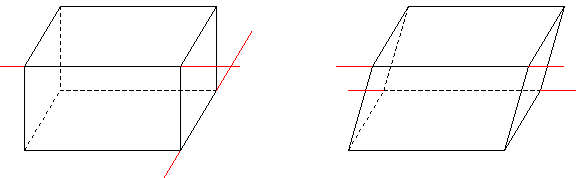
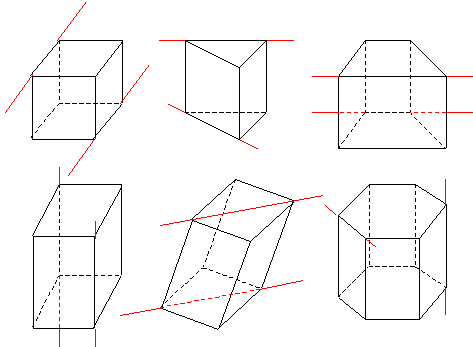
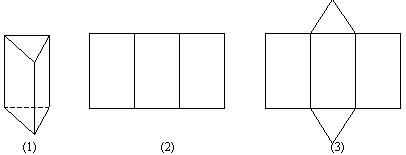
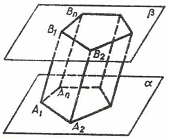
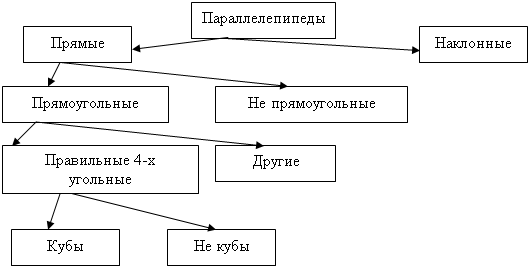
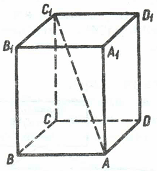
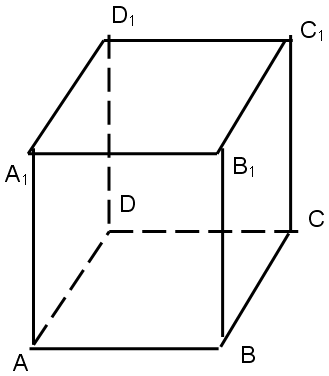
Определение. Многогранник, две грани которого - одноименные многоугольники, лежащие в параллельных плоскостях, а любые два ребра, не лежащие в этих плоскостях, параллельны, называется призмой.
1. Краткий обзор развития геометрии
1.1 Общий исторический обзор
Первые геометрические понятия возникли в доисторические времена. Разные формы материальных тел наблюдал человек в природе: формы растений и животных, гор и извилин рек, круга и серпа Луны и т. п. Однако человек не только пассивно наблюдал природу, но практически осваивал и использовал ее богатства. В процессе практической деятельности он накапливал геометрические сведения. Материальные потребности побуждали людей изготовлять орудия труда, обтесывать камни и строить жилища, лепить глиняную посуду и натягивать тетиву на лук. Конечно, десятки и сотни тысяч раз натягивали люди свои луки изготовляли разные предметы с прямыми ребрами и т. п., пока постепенно дошли до отвлеченного понятия прямой линии. Примерно то же можно сказать о других основных геометрических понятиях. Практическая деятельность человека служила основой длительного процесса выработки отвлеченных понятий, открытия простейших геометрических зависимостей и соотношений.
Начало геометрии было положено в древности при решении чисто практических задач. Со временем, когда накопилось большое количество геометрических фактов, у людей появилось потребность обобщения, уяснения зависимости одних элементов от других, установления логических связей и доказательств. Постепенно создавалась геометрическая наука. Примерно в VI - V вв. до н. э. в Древней Греции в геометрии начался новый этап развития, что объясняется высоким уровнем, которого достигла общественно-политическая и культурная жизнь в греческих государствах. Произведения, содержащие систематическое изложение геометрии, появились в Греции еще в V до н.э., но они были вытеснены “Началами” Евклида.
Геометрические знания примерно в объеме современного курса средней школы были изложены еще 2200 лет назад в “Началах” Евклида. Конечно, изложенная в “Началах” наука геометрия не могла быть создана одним ученым. Известно, что Евклид в своей работе опирался на труды десятков предшественников, среди которых были Фалес и Пифагор, Демокрит и Гиппократ, Архит, Теэтет, Евдокс и др. Ценой больших усилий, исходя из отдельных геометрических сведений, накопленных тысячелетиями в практической деятельности людей, эти великие ученые сумели на протяжении 3 - 4 столетий привести геометрическую науку к высокой ступени совершенства. Историческая заслуга Евклида состоит в том, что он, создавая свои “Начала”, объединил результаты своих предшественников, упорядочил и привел в одну систему основные геометрические знания того времени. На протяжении двух тысячелетий геометрия изучалась в том объеме, порядке и стиле, как она была изложена в “Началах” Евклида. Многие учебники элементарной геометрии во всем мире представляли (а многие и поныне представляют) собой лишь переработку книги Евклида. “Начала” на протяжении веков были настольной книгой величайших ученых.
В XVII в. Декарт благодаря методу координат сделал возможным изучение свойств геометрических фигур с помощью алгебры. С этого времени начала развиваться аналитическая геометрия. В XVII - XVIII вв. зарождается и разрабатывается дифференциальная геометрия, изучающая свойства фигур с помощью методов математического анализа. В XVIII- XIX вв. развитие военного дела и архитектуры привело к разработке методов точного изображения пространственных фигур на плоском чертеже, в связи с чем появляются начертательная геометрия, научные основы которой заложил французский математик Г. Монж, и проективная геометрия, основы которой были созданы в трудах французских математиков Д.Дезарга и Б.Паскаля (XVII в.). В ее создании важнейшую роль сыграл другой французский математик - Ж. В. Понселе (XIX в.).
Коренной перелом в геометрии впервые произвел в первой половине ХIХ в. великий русский математик Николай Иванович Лобачевский, который создал новую, неевклидову геометрию, называемую ныне геометрией Лобачевского.
Открытие Лобачевского было началом нового периода в развитии геометрии. За ним последовали новые открытия немецкого математика Б. Римана и др.
В настоящее время геометрия тесно переплетается со многими другими разделами математики. Одним из источников развития и образования новых понятий в геометрии, как и в других областях математики, являются современные задачи естествознания, физики и техники.
Похожие работы
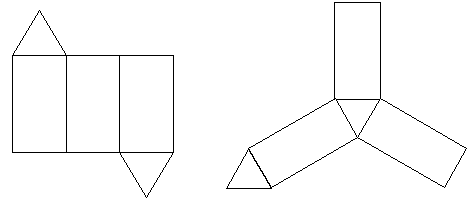
... , перпендикулярности прямой и плоскости в пространстве. III этап: Введение понятия развертки призмы (поверхности) Цель: Расширение знаний учащихся связанных с общим понятием призмы. Ввести понятие развертки (опираясь на понятие развертки прямого параллелепипеда на уроках черчения, труда). Оборудование: Картонные модели призм, ножницы, раскладные модели призм. Перед учениками на партах находятся ...
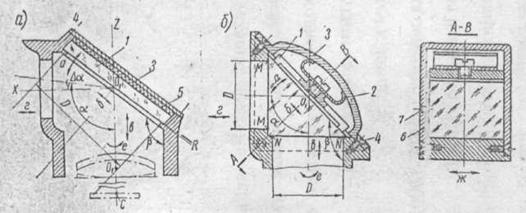
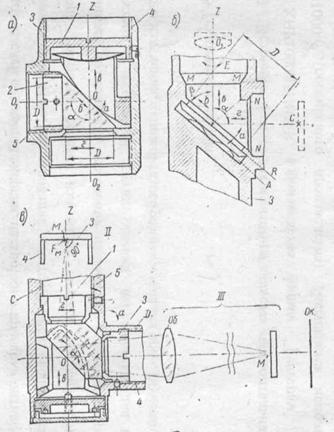
... оптикой следят за тем, чтобы не загрязнить оптические детали пальцами рук и инструментом. Губки пинцетов и другие металлические инструменты должны быть обклеены замшей или резиновыми пластинками, а затем обезжирены. 2. Сборка зеркал и призм в оправах Общие сведения Узлы крепления зеркал и призм конструктивно более разнообразны, чем сборки круглой оптики. Ввиду конструктивной простоты ...
... параллелепипеда рёбер Варианты ответов: А Б В Г Д 8 10 12 24 6 3. Многогранник, составленный из двух равных многоугольников и , расположенных в параллельных плоскостях, и n параллелограммов …, , называется: А) параллелепипед; Б) призма; В) пирамида; Г) многогранник; Д) конус. 4. Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого ...
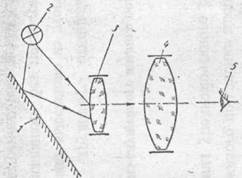
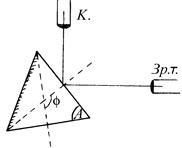
... желтая 0,579 4 зеленая 0,546 5 сине-зеленая 0,492 6 синяя 0,436 7 фиолетовая 0,405 Определение дисперсии и разрешающей силы стеклянной призмы Используя данные упражнения 2, постройте график зависимости показателя преломления от длины волны n = f (l) (указания: ...
0 комментариев