Навигация
Положим множество V={S} и i=1
1. Положим множество V={S} и i=1.
2. Положим множество Vi = Vi-1{A P и A Vi-1 }.
3. Если Vi Vi-1, то i=i=1 и перейти к шагу 2. В противном случае
N’= N Vi , T’=TVi. Искомое множество продукций Р’ состоит
из множества продукций Р, содержащих символы из множества Vi
АЛГОРИТМ УСТРАНЕНИЯ БЕСПОЛЕЗНЫХ СИМВОЛОВ.
Пусть дана КС-грамматика G={N,T,P,S}. Построим эквивалентную грамматику G’={N’, T’, P’, S} без бесполезных символов. Метод состоит в следующем:
1. Положим N0=, i=1.
2. Положим множество Ni=Ni-1{A | A, i-1)}.
3. Если NiNi-1, положим i=i+1 и перейти к шагу 2. В противном случае положим N0=Ni.
4. Положим G1={N0 N,T,P’,S}, где P’P состоит из продукций множества Р, содержащих символы из N0.
5. Применив к G1 алгоритм устранения в грамматике недостижимых символов, получим G’={N’, T’, P’, S}.
АЛГОРИТМ ПРЕОБРАЗОВАНИЯ ГРАММАТИКИ В
ГРАММАТИКУ БЕЗ -ПРОДУКЦИЙ.
Пусть дана КС-грамматика G={N,T,P,S}. Построим -свободную грамматику G’, эквивалентную грамматике G. Метод состоит в следующем.
1. Применяем шаги 1-3 алгоритма устранения бесполезных символов, определяем множество N0={ A | A, A}.
2. Множество P’ строим следующим образом. Если продукция A0B11B22...Bkk , где k и Bi 0, но ни один символ в цепочках j (0 j k) не принадлежит N0, добавим к Р’ продукции вида A01122...kk, где Xi есть или Bi или , не включая в P’ продукцию A.
Если S0, то включим в P’ продукцию вида S’ | S, где S’ новый нетерминальный символ и положим N’=NS’, в противном случае N’=N, S’=S.
3. Положим G’={N’,T’, P’, S’}.
АЛГОРИТМ УСТРАНЕНИЯ ЦЕПНЫХ ПРОДУКЦИЙ.
Пусть нам дана -свободная КС-грамматика G={N,T,P,S}. Получим эквивалентную КС-грамматику G’={N’, T’, P’, S’} свободную от цепных и -продукций.
Метод состоит в следующем.
1. Для каждого A построим множество NA={B | A} нетерминальных символов, выводимых из А следующим образом:
1.1. Положим N0={A} и i=1;
1.2. Положим Ni={C | BC и Вi-1} i-1;
1.3. Если Ni i-1, то положим i=i+1 и повторим шаг 1.2. В противном случае положим NA=N.
2. Построим множество P’: если (В) и не является цепной продукцией, то включим в P’ продукцию A, для всех таких А, что ВА.
3. Положим G={N, T, P’,S}.
Данный алгоритм позволяет устранить из грамматики и циклы, т.е. выводы А*, где А.
УСТРАНЕНИЕ В КС-ГРАММАТИКЕ ЛЕВОЙ РЕКУРСИИ.
Алгоритмы синтаксического анализа легче строить тогда, когда КС-грамматика G не обладает свойствами леворекурсивности, т.е. в ней нет продукций вида X. Это особенно важно при использовании методов разбора сверху вниз и слева направо. Выбор продукции из множества альтернативных в этих методах базируется на сравнении порождённого крайнего левого символа промежуточной цепочки с текущим символом входной терминальной цепочки. При появлении же в выводе левой рекурсии произойдёт зацикливание. Поэтому при использовании алгоритмов нисходящего разбора левую рекурсию необходимо удалить.
В общем случае левая рекурсия в КС-грамматике может быть явной, когда есть продукции вида A или неявной- когда в грамматике есть взаимно рекурсивные продукции вида:
A|...
B|...
Устранение леворекурсивных правил. Пусть G КС-грамматика, в которой есть леворекурсивные правила. Эквивалентная грамматика G’ получается путём замены множества леворекурсивных правил грамматики G на множество правил вида:
A1’|2’| ... |n’
A’1’|2’| ... |n|
Здесь А’- новый вспомогательный нетерминальный символ.
ДЕТЕРМИНИРОВАННЫЙ СИНТАКСИЧЕСКИЙ АНАЛИЗ
СВЕРХУ ВНИЗ
В данном синтаксическом анализе используются LL(1) грамматики, которые являются обобщением S-грамматик.
КС-грамматика называется S-грамматикой, если выполняются условия:
-правая часть каждой продукции начинается терминальным символом;
-если две или более продукций имеют совпадающие левые части, то правые части этих продукций должны начинаться с различных терминальных символов.
Для заданной S-грамматики магазинный автомат ( МП-распознаватель) с одним состоянием задаётся следующим образом:
1. А=Т{|-}
2. Г=N{t | t и (Аt)}{}.
3. Q={q}.
4. z0={#S | S- аксиома}.
5. q0=q.
6. Каждой продукции КС-грамматики сопоставляется элемент управляющей таблицы МП-распознавателя. Если продукция имеет вид At, где A и t, а {}, то этому правилу в строке А и в столбце t будут соответствовать операции
ЗАМЕНИТЬ (r), СДВИГ
где r - цепочка , записанная в обратном порядке для того, чтобы удовлетворить соглашения «верхний символ справа».
Если продукция имеет вид Аt, то строке А и столбцу t соответствуют операции
ЧТЕНИЕ, СДВИГ.
Если магазинным символом является терминал b, то элементом таблицы в строке b будет
ЧТЕНИЕ, СДВИГ.
Элементом таблицы, который находится в строке маркера дна магазина # и концевого маркера |-, является
ДОПУСТИТЬ.
Все остальные элементы таблицы заполняются операцией
ОТВЕРГНУТЬ.
где: А- символы, записанные на входной ленте;
Г- символы, записанные в магазинную память;
Q- множество состояний автомата;
z0- начальная запись в магазин;
q0-начальное состояние автомата.
S-грамматики хотя и допускают детерминированный нисходящий разбор, описывают достаточно узкий класс языков. естественным расширением этого класса было бы - разрешить, чтобы первый символ в правых частях продукций этой грамматики мог быть нетерминалом, но при этом грамматика всё же допускала детерминированный разбор.
Определим ПЕРВ() как множество терминальных символов, которые являются первыми символами цепочек, выводимых из .
Цепочка называется аннулирующей, если .
Продукция грамматики вида А также называется аннулирующим.
ВЫБОР (А)= ПЕРВ(),
если - не аннулирующая, и
ВЫБОР(А)=ПЕРВ()СЛЕД(А),
если - аннулирующая цепочка. При этом СЛЕД(А) - множество следующих за А терминалов в промежуточной цепочке, выводимой из S|-, где S-аксиома грамматики.
Для того, чтобы КС-грамматика была типа LL(1), необходимо, чтобы множества выбора для правил с одинаковыми левыми частями не пересекались, т.е. не имели общих терминальных символов.
Если для вашей грамматики это так, то она будет относится к типу LL(1) и для неё автомат строится по следующему правилу.
ПРАВИЛА ОПРЕДЕЛЕНИЯ ДЕТЕРМИНИРОВАННОГО
МП-РАСПОЗНАВАТЕЛЯ ПО LL(1) ГРАММАТИКЕ.
Для заданной LL(1) грамматики МП-распознаватель задаётся следующим образом:
1. А=Т{|-};
2. Г=N{t | t и (Аt), , {}}{};
3. Q={q};
4. z0={#S};
5. q0=q;
6. Управление описывается управляющей таблицей с одним состоянием, строки помечены магазинными символами из Г, столбцы - входными символами из А. Элемент таблицы создаётся для каждой продукции. Если продукция имеет вид Аt, то этому правилу в строке А и столбце t будут соответствовать операции
ЗАМЕНИТЬ(r), СДВИГ,
где r - цепочка , записанная в обратном порядке для того, чтобы удовлетворить соглашению «верхний символ справа»
Если продукция имеет вид А, где =Х и Х, {}*, то ему в строке А и во всех столбцах, принадлежащих множеству ВЫБОР (А), будет соответствовать переход
ЗАМЕНИТЬ (r), ДЕРЖАТЬ.
Когда =, вместо ЗАМЕНИТЬ() можно использовать ЧТЕНИЕ.
Если продукция имеет вид Аt, то ей в строке А и в столбце t соответствует операция
ЧТЕНИЕ. СДВИГ.
7. Если магазинным символом является терминал b, то элементом таблицы в строке b будет
ЧТЕНИЕ. СДВИГ.
8. Элементом таблицы, который находится в строке маркера дна # и столбце концевого маркера |-, является
ДОПУСТИТЬ.
9. Все остальные элементы таблицы заполняются операцией
ОТВЕРГНУТЬ.
5. Содержание отчёта.
Отчёт составляется каждым студентом и содержит развёрнутые ответы на все пункты задания. К отчёту прилагается таблица переходов МП-распознавателя и работающая программа МП-распознавателя.
6. Контрольные вопросы.
1. Как определяется КС-грамматика?
2. Как определяется нормальная форма Хомского?
3. Как задаётся нормальная форма Грейбах?
4. Как исключить -продукции?
5. Как устранить недосигаемые символы?
6. Как устранить бесполезные символы?
7. Как устраняются циклические связи в продукциях?
8. Как устранить левые рекурсии в грамматике?
9. Как определяется магазинный автомат?
10. Как определяется LL(1) грамматика?
11. Как определяется S-грамматика?
Литература.
1. Компаниец Р.И., Маньков Е.В., Филатов Н.Е. Основы построения трансляторов. -СПб.: КОРОНА принт, 2000. -256 с.
2. Хантер Р. Проектирование и конструирование компиляторов. М.: Финансы и статистика. 1984 г.
3. Грис Д. Конструирование компиляторов для цифровых вычислительных машин. М.: Мир,1975 г.
Похожие работы
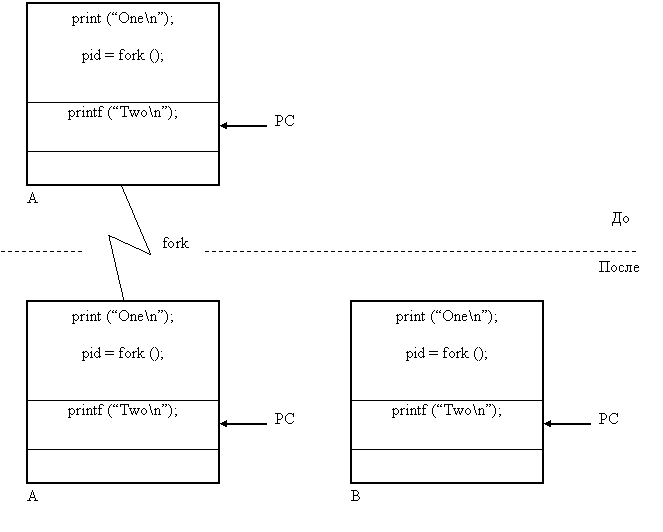
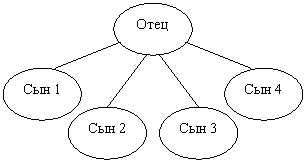
... процессом init (процесс, идентификатор которого pid = 1, становится их новым родителем). Порядок выполнения работы 1. Изучить теоретическую часть лабораторной работы. 2. Организовать функционирование процессов следующей структуры: 2.1. Отец формирует нумерованные сообщения вида: N pid time (N –текущий номер сообщения, pid – pid процесса, time – время записи в формате мм.сс (минуты. ...
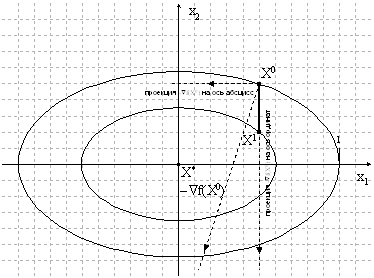
... работы со справочной системой работа практикума приостанавливается. 3. Организационно-экономическое обоснование проекта В ходе дипломного проекта был разработан компьютерный лабораторный практикум по курсу «Теория оптимизации и численные методы». В данном разделе рассмотрена экономическая сторона проекта. Рассмотрены следующие вопросы: 1) сетевая модель 2) расчёт ...
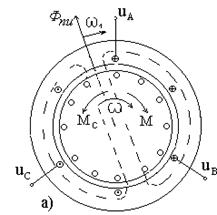
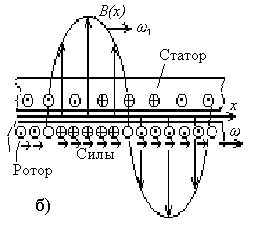
... концентрических окружностей с уменьшающимся радиусом по мере затухания колебаний скорости и момента. Аналогичная картина наблюдается при ступенчатом набросе нагрузки. 5. РАЗРАБОТКА ВИРТУАЛЬНОЙ ЛАБОРАТОРНОЙ РАБОТЫ НА БАЗЕ ВИРТУАЛЬНОЙ АСИНХРОННОЙ МАШИНЫ Иную возможность анализа АД представляет специализированный раздел по электротехнике Toolbox Power System Block. В его библиотеке имеются блоки ...
... гистерезисная диаграмма поляризации сегнетоэлектрика. Подобрать масштаб по вертикальной оси осциллографа так, чтобы изображение занимало весь экран. Внимание: в процессе выполнения последующих пунктов лабораторной работы не допускается изменять положение масштабного переключателя осциллографа. Измерить и записать в табл. 6.2 координаты вершины гистерезисного цикла: xm, ym (координаты вершины ...

0 комментариев