Навигация
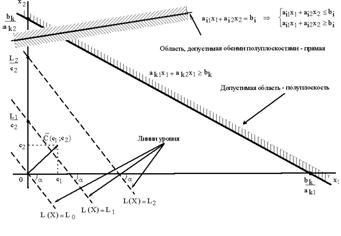
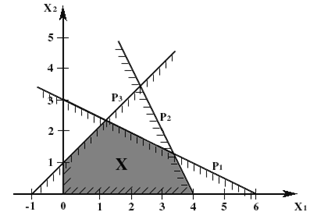
Основной случай - получающаяся область имеет вид ограниченного выпуклого многоугольника (рис. 3а))
1. Основной случай - получающаяся область имеет вид ограниченного выпуклого многоугольника (рис. 3а)).
2. Неосновной случай - получается неограниченный выпуклый многоугольник, имеющий вид, подобный изображенному на рис. 3.б. Подобная ситуация, например, получится, если в рассмотренном выше примере убрать ограничение . Оставшаяся часть будет неограниченным выпуклым многоугольником.
|
|
|
Наконец, возможен случай, когда неравенства (1.31) противоречат друг другу, и допустимая область вообще пуста.
Рассмотрим теорию на конкретном примере:
Найти допустимую область задачи линейного программирования, определяемую ограничениями
| (1.32) |
Решение:
1. Рассмотрим прямую . При , а при . Таким образом, эта прямая проходит через точки (0,1) и (-1,0). Беря получим, что -0+0<1 и поэтому интересующая нас полуплоскость лежит ниже прямой, изображенной на рис. 4.а.
2. Рассмотрим прямую . При , а при . Таким образом, эта прямая проходит через точки (0, -1/2) и (1,0). так как (4.б).
3. Наконец, рассмотрим прямую . Она проходит через точки (0,3) и (3,0) и так как 0+0<3, то интересующая нас полуплоскость лежит ниже прямой, изображенной на рис. 4.в.
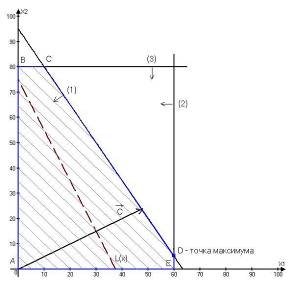
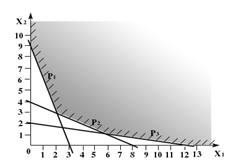
Сводя все вместе и добавляя условия получим рисунок 5, где выделена область, в которой выполняются одновременно все ограничения (1.32). Обратите внимание на то, что получившаяся область имеет вид выпуклого многоугольника.
Этап 2.
Вернёмся теперь к исходной задаче линейного программирования. В ней, кроме системы неравенств, есть еще целевая функция .
|
Рассмотрим прямую. Будем увеличивать L. Что будет происходить с нашей прямой?
Легко догадаться, что прямая будет двигаться параллельно самой себе в том направлении, которое дается вектором , так как это - вектор нормали к нашей прямой и одновременно вектор градиента функции .
А теперь сведем всё вместе. Итак, надо решить задачу
Oграничения задачи вырезают на плоскости некоторый многоугольник. Пусть при некотором L прямая пересекает допустимую область. Это пересечение дает какие-то значения переменных , которые являются планами.
Этап 3
Увеличивая L мы начнем двигать нашу прямую и её пересечение с допустимой областью будет изменяться (см. рис. 7). В конце концов эта прямая выйдет награницу допустимой области - как правило, это будет одна из вершин многоугольника. Дальнейшее увеличение L приведёт к тому, что пересечение
|
прямой с допустимой областью будет пустым. Поэтому то положение прямой , при котором она вышла на граничную точку допустимой области, и даст решение задачи, а соответствующее значение L и будет оптимальным значением целевой функции.
1.4 Примеры задач, решаемых графическим методом.
Пример:
Решить задачу
| (1.41) |
Решение
Допустимую область мы уже строили - она изображена на рис. 5.
Повторим еще раз этот рисунок, оставив только допустимую область и
нарисовав дополнительно прямые (см. рис. 8).
|
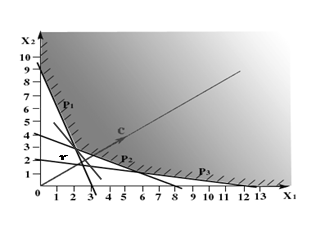
Пусть, например, L=2. Тогда прямая проходит через точки (2,0) и (0,1) и изображена на рис. 8. Будем теперь увеличивать L. Тогда прямая начнёт двигаться параллельно самой себе в направлении, указанном стрелкой. Легко догадаться, что максимальное значение L получится тогда, когда прямая пройдет через вершину многоугольника, указанную на рисунке, и дальнейшее увеличение L приведет к тому, что прямая выйдет за пределы многоугольника и её пересечение с допустимой областью будет пустым.
Выделенная вершина лежит на пересечении прямых
и поэтому имеет координаты . Это и есть решение нашей задачи, т.е. есть оптимальный план задачи (1.41). При этом значение целевой функции , что и дает её максимальное значение.
Обратите внимание на то, что оптимальный план, как правило, соответствует какой-то вершине многоугольника, изображающего допустимую область. И лишь в том случае, когда прямая случиться так, что решение не будет единственным. Но и в этом случае вершины, соответствующие границам этой стороны, дают оптимальные планы нашей задачи линейного программирования. Таким образом, вершины допустимой области играют в решении задач линейного программирования особую роль.
|
Ну, а если допустимая область неограничена, то и значение целевой функции может быть неограниченным.
Подводя итог этим примерам, можно сформулировать следующие положения:
1. допустимая область - это выпуклый многоугольник;
2. оптимум достигается в вершине допустимой области (если допустимая область ограничена и не пуста);
3. ограниченность целевой функции в допустимой области является необходимым и достаточным условием разрешимости задачи.
Гл 2 Решение задач линейного программирования графическим способом на ЭВМ 2.1 Описание работы программы
Программа написана с использованием собственных функций и процедур и трех стандартных модулей System, Crt и Graph.
При запуске программы она проверяет возможно ли использование графического интерфейса. Если это возможно то программа переходит к следующему этапу.
Далее процедурой ShowXOY Рисуется на экран координатные оси. На этом работа этой процедуры заканчивается и пользователь в следующей процедуре (EnterNerav и в частности в подпроцедуре GetNerav) предлагается ввести коэффициенты неравенства a1x+a2y=b в следующем порядке: a1 пробел a2 пробел b. Сразу после ввода всех коэффициентов процедурой ShowLine рисуется нужная линия. После нажатия [Esc] процедура EnterNerav заканчивается и передает управление процедуре EnterMainF в которой пользователю предлагается ввести коэффициенты целевой функции. Далее работа переходит к процедуре GetResult где идет подсчет оконцательного товета с помощбю процедуры SolveOprtel где считаетя определитель т. е. точки пересечения целевой функции с каждой линией ограничения. Далее выводится ответ, если это возможно.
Далее следует описание используемых стандартных процедур и функций.
Процедуры и функции модуля System:
Function Frac(X : Real) : Real;
Возвращает дробную часть аргумента.
Параметр X - выражение вещественного типа. Результат - дробная часть X, то есть Frac(X) = X-Int(X).
Procedure Str(X [: Width [: Decimals ]]; Var S : String);
Преобразовывает число в строку. Преобразовывает числовое значение X в строковое представление этого числа, которое можно выводить операторами типа Write и OutText.
Function Round(X : Real) : Longint;
Округляет значение вещественного типа до значения целочисленного типа. X - выражение с реальным типом. Round возвращает значение типа Longint, которое является значением X, округленного к самому близкому целому числу. Если X – ровно посередине между двумя целыми числами, то результатом будет число с самой большой абсолютной величиной.
Если округленное значение X ненаходится внутри допустимого диапазона Longint, то происходит ошибка во время выполнения программы.
Модуль Crt:
В модуле Crt находятся мощные подпрограммы, которые дают вам возможность полного управления возможностями вашего PC.
Подпрограммы модуля Crt обеспечивают контроль над текстовыми режимами экрана, расширенными кодами клавиатуры, цветами, окнами и звуком.
Crt может использоваться только в программах, предназначенных для IBM PC, AT, PS/2 и полностью совместимых.
Procedure Read( [ var F : Text; ] V1 [ , V2, …, VN ]); (текстовые файлы)
Читает одну или более величин из текстового файла в одну или более переменных. Параметры: F - необязательная переменная текстового файла, если не указана, то используется стандартная переменная Input; V1,...,VN - переменные типа Char, Integer, Real или String.
В случае переменной типа Char процедура Read считывает из файла один символ и присваивает его переменной. В случае переменной целого типа процедура Read ожидает поступления последовательности символов, образующих число со знаком, согласно принятому в Паскале синтаксису. Любые пробелы, знаки табуляции или метки конца строки, предшествующие числовой строке, пропускаются. Считывание прекращается при обнаружении первого пробела, символа табуляции или метки конца строки, которые следуют за числовой строкой, или в том случае, если функция Eof(F) принимает значение True. Если числовая строка не соответствует ожидаемому формату, то происходит ошибка ввода-вывода, в противном случае переменной присваивается считанное значение. Если Eof(F) принимала значение True перед выполнением процедуры Read, или Eof(F) приняла значение True при пропуске начальных пробелов, знаков табуляции или меток конца строки, то переменной присваивается нулевое значение. Следующая операция Read начнется с пробела, символа табуляции или метки конца строки, которыми завершилась числовая строка.
В случае переменной вещественного типа процедура Read ожидает поступления последовательности символов, которые образуют число со знаком в соответствии с принятым в Паскале синтаксисом за исключением того, что шестнадцатиричное представление не допускается. Любые пробелы, знаки табуляции или метки конца строки, предшествующие числовой строке, пропускаются. Считывание прекращается при обнаружении первого пробела, символа табуляции или метки конца строки, которые следуют за числовой строкой или в том случае, если функция Eof(F) принимает значение True. Если числовая строка не соответствует ожидаемому формату, то происходит ошибка ввода-вывода, в противном случае переменной присваивается считанное значение.
Если Eof(F) принимало значение True перед выполнением процедуры Read, или Eof(F) приняло значение True при пропуске начальных пробелов, знаков табуляции или меток конца строки, то переменной присваивается нулевое значение. Следующая операция Read начнется с пробела, символа табуляции или метки конца строки, которыми завершилась числовая строка.
Procedure Write( [ var F : Text; ] P1 [ , P2,…, PN ] ); (текстовые файлы) Записывает одну или более величин в текстовый файл. F - переменная текстового файла, если не указана, то предполагается использование стандартной файловой переменной Output, P1,...,PN - параметры записи, которые содержат выводимые выражения типов Char, Integer, Real, String, Packed String или Boolean. Параметр записи также может содержать спецификацию ширины поля и количество десятичных знаков. Параметр записи имеет следующий вид: OutExpr [ : MinWidth [ : DecPlaces ] ], где OutExpr представляет собой выводимое выражение, MinWidth - целое число, задающее минимальную ширину поля, которая должна быть больше нуля. Записывается ровно столько символов, сколько определено в MinWidth (при необходимости используются ведущие пробелы) за исключением случаев, когда OutExpr имеет значение, которое должно быть представлено большим количеством символов, чем указано в MinWidth. В этом случае записывается количество символов, достаточное для представления выводимой величины. Аналогично, если параметр MinWidth опущен, то записывается необходимое количество символов. DecPlaces задает число десятичных знаков в представлении вещественного значения с фиксированной точкой. Оно может указываться только в том случае, если OutExpr имеет тип Real, и указан параметр MinWidth. Если параметр MinWidth указан, то он должен быть больше или равен нулю.
Модуль Graph находится библиотека, состоящая из более чем 50 графических подпрограмм от побитовых до подпрограмм высокого уровня.
Procedure SetColor(Color : Word);
Устанавливает текущий цвет, используя палитру. SetColor(5) делает пятый цвет в палитре цветом текущего рисунка. Цвет может быть задан числом от 0 до 15 (для стандартных драйверов), в зависимости от текущего графического драйвера и текущего графического режима.
Procedure Line(X1, Y1, X2, Y2 : Integer);
Рисует линию из точки с координатами (X1, Y1) в точку с координатами (X2, Y2). Рисует линию стилем и толщиной, определенными SetLineStyle и использует цвет, установленный обращением к процедуре SetColor.
Последовательность операторов
MoveTo(100, 100); LineTo(200, 200);
является эквивалентной
Line(100, 100, 200, 200); MoveTo(200, 200);
Procedure OutTextXY(X, Y : Integer; TextString : String);
Посылает строку на устройство вывода. Отображает TextString в позиции (X, Y). Строка TextString усекается на границе области просмотра, если она слишком длинная. Если один из штриховых шрифтов активен, то строка TextString усекается на границе экрана, если она слишком длинная. Если заданный по умолчанию (растровый шрифт активен, и строка слишком длинная, чтобы поместиться на экране, то текст не отображается вообще.
Процедура OutTextXY использует набор шрифтов SetTextStyle. Чтобы поддерживать совместимость кода при использовании нескольких шрифтов, используйте TextWidth и TextHeight для определения размера строки.
Procedure SetFillStyle(Pattern : Word; Color : Word);
Устанавливает цвет и стиль закраски. Устанавливает шаблон и цвет для всех операций закраски, производимых FillPoly, Bar, Bar3D и PieSlice. Доступно несколько предопределенных шаблонов закраски. Заданный по умолчанию шаблон = Solid и заданный по умолчанию цвет - цвет с максимальным номером в палитре. Если в SetFillStyle переданы недопустимые параметры, то в переменной GraphResult возвращается значение grError, и текущие установки закраски не будут изменены.
Если Pattern равняется UserFill, то активным шаблоном закраски станет шаблон, определяемый пользователем (устанавливаемый с помощью процедуры SetFillPattern).
Procedure FloodFill(X, Y : Integer; Border : Word);
Закрашивает замкнутую область, используя текущие стиль и цвет закраски. Закрашивает замкнутую область на растровых устройствах. Точка с координатами (X, Y) - начальная точка внутри замкнутой области, с которой начнется закраска. Текущий шаблон закраски устанавливается процедурами SetFillStyle и SetFillPattern. Закрашивается область, ограниченная цветом с номером Border. Если точка (X, Y) находится внутри замкнутой области, то закраска будет происходить внутри области. Если же эта точка находится снаружи замкнутой области, то будет закрашено все пространство вне области.
Более подробное описание программы содержится в комментариях к исходному тексту.
2.1 Текст программы{$A+,B-,D+,E+,F-,G-,I+,L+,N+,O+,P-,Q-,R-,S+,T-,V+,X+}
{$M 16384,0,655360}
program Kurs1;{Геометрическая интерпретация решения задач}
uses
CRT, Graph;{используемы модули}
{Типы}
type
TNerav = record{коэффициенты неравенств а1х+а2y<=b}
x: Real;{a1}
y: Real;{a2}
b: Real; {b}
end;
TMatrix = array[1..100] of TNerav;{Количество неравенств}
{Константы}
const
MaxX: Integer = 640-30; {максимальное значение X на экране}
MaxY = 20; {максимальное значение Y на экране}
MinX = 40; {x=0 минимальное значение X на экране}
MinY: Integer = 480-40;{y=0 минимальное значение Y на экране}
MASHT = 15; {Масштаб при 15: maxY=28, MaxX=38}
STEP = 1; {шаг изменения свободного члена целевой функчии}
{Переменные}
var
Gd, Gm: Integer; {Иниц. гафики}
Matr: TMatrix; {Матрица неравенств}
c: Real; {Свободный член целевой ф-ии}
N: TNerav; {Коэффициенты неравенств}
i: 0..100; {Счетчик кол-ва неравенств}
MainF: TNerav; {Коэффициенты целевой ф-ии}
XResult,YResult: Real; {Ответ(кординаты)}
procedure ShowXOY;{Проц. показа координатных осей}
Begin
SetColor(White);
Line(MinX, MaxY,MinX-4, MaxY+7);{стрелочки у Y}
Line(MinX, MaxY,MinX+4, MaxY+7);
OutTextXY(MinX-15, MaxY, 'У');
MoveTo(MinX, MaxY);
LineTo(MinX, MinY);{Сами оси}
LineTo(MaxX, MinY);
Line(MaxX, MinY, MaxX-7, MinY-4);{стрелочки у X}
Line(MaxX, MinY, MaxX-7, MinY+4);
OutTextXY(MaxX, MinY+5, 'X');
End;
procedure ShowLine(_iN:TNerav);
var s: String;
Begin
if _iN.b/_iN.y<0 then begin{если коэффиц. при Y меньше 0}
MoveTo(MinX+Round((_iN.b-(Round(MinY/MASHT)*_iN.y))/_iN.x*MASHT),MaxY);
SetColor(15);
LineTo(MinX+Round(_iN.b/_iN.x*MASHT),MinY);
end;
if _iN.b/_iN.x<0 then begin{если коэффиц. при X меньше 0}
MoveTo(MinX,MinY-Round(_iN.b/_iN.y*MASHT));
SetColor(15);
LineTo(MaxX,MinY-Round((_iN.b-(Round(MaxX/MASHT)*_iN.x))/_iN.y*MASHT));
end;
SetColor(LightGreen);
Str(_iN.b/_iN.x:3:1,s);
OutTextXY(MinX+Round(_iN.b/_iN.x*MASHT),MinY+5,s);{рисуем значения на оси OX}
Str(_iN.b/_iN.y:3:1,s);
OutTextXY(MinX-40,MinY-Round(_iN.b/_iN.y*MASHT),s);{рисуем значения на оси OY}
MoveTo(MinX,MinY-Round(_iN.b/_iN.y*MASHT));
SetColor(15);{Рисуем саму линию}
LineTo(MinX+Round(_iN.b/_iN.x*MASHT),MinY);
End;
procedure EnterNerav;{процедура ввода неравенств до нажатия Esc}
procedure GetNerav;{подпроцедура ввода коэф-тов одного неравенства}
var j,k: Real;
Begin
repeat
SetFillStyle(1,0); Bar(0,0,GetMaxX,MaxY-1);
OutTextXY(7,3,'Введите коэффициенты неравенств: ');
Window(34,1,80,1);
Read(N.x, N.y, N.b);{вводим коэффициенты}
j:=N.x;
k:=N.y;
repeat{далее идет сокращение коэффициентов если это возможно}
if (Frac(N.b / j) = 0) then
if (Frac(N.x / j) = 0) then Break;
j:=j-1;
until (j<=0);
if J>=0 then
repeat
if (Frac(N.b / k) = 0) then begin
if (Frac(N.y / k) = 0) then
if (j=k) then begin
N.b:=N.b / k;
N.x:=N.x / k;
N.y:=N.y / k;
Break;
end
end;
k:=k-1;
until (k<=0);
until (N.x<>0) and (N.y<>0); {Ограничение чтоб небыло нулей}
Inc(i); {Увеличиваем счетчик}
Matr[i]:=N;{Добавляем в матрицу коэффициенты}
ShowLine(N);{Вызываем процедуру рисования линии}
SetFillStyle(1,0); Bar(0,0,GetMaxX,MaxY-1);
OutTextXY(7,3,'Ввести еще? (Enter=Да/Esc=Нет)');
End;
var
Key:Char;
Begin
GetNerav;
repeat
key:=#0;
if KeyPressed then begin
key:=ReadKey;
case key of
#13: GetNerav;{ввод еще одного нер-ва}
end;
end;
Until Key in [#27];{до нажатия Esc}
End;
procedure EnterMainF;
{эта процедура предлагает выбрать пользователю выбрать выход из ОДЗ}
var key: Char;
j: 0..100;
S: String;
Begin
SetFillStyle(3,1); FloodFill(MinX+1, MinY-1, 15);
SetFillStyle(1,0); Bar(0,0,GetMaxX,MaxY-1);
SetColor(White);
OutTextXY(7,3,'Введите коэффициенты целевой функции: ');
Window(40,1,80,25); Read(MainF.x, MainF.y);
End;
procedure GetResult;
var
k,j: 0..100;
X: Real;
Y: Real;
XTmp: Real;
YTmp: Real;
cTmp: Real;
boolAnswer: Boolean;
key: Char;
STmp: String;
Result: String;{Строка для вывода на экра результата}
procedure SolveOprtel(inN, inMainF: TNerav; ic:Real; var outX, outY: Real);
{в этой подпроцедуре подностью вычисляется определитель}
var
_d: Real;{Дельта определителя}
dx: Real;{Дельта X определителя}
dy: Real;{Дельта Y определителя}
Begin
_d:=(inN.x*(inMainF.y)) - (inN.y*inMainF.x);
dx:=(inN.b*(inMainF.y)) - (inN.y*ic);
dy:=(inN.x*ic) - (inN.b*inMainF.x);
if _d <> 0 then begin{исклюсаем бесчисленное мн-во решений}
outX:=dx/_d;
outY:=dy/_d;
end;
if (_d = 0) and ((dx = 0) xor (dy = 0)) then begin{исклюсаем - нет решений}
SetColor(Red);
OutTextXY(300,230,'Нет решений!!!');
ReadKey;
CloseGraph;
Halt;
end;
End;
Begin
Bar(0,0,GetMaxX,MaxY-1);
SetColor(White);
OutTextXY(7,3,'Пожалуйста подождите... (Esc - Отмена)');
{считаем координаты выхода}
c:=0;
cTmp:=0;
repeat
if i=1 then SolveOprtel(Matr[1], MainF, c, XResult, YResult)
else
for j:=1 to i-1 do begin
SolveOprtel(Matr[j], MainF, c, XTmp, YTmp);
for k:=j+1 to i do begin
SolveOprtel(Matr[k], MainF, c, X, Y);
if X=XTmp then XResult:=X;
if Y=YTmp then YResult:=Y;
end;
end;
{далее мы находим максимум функции}
BoolAnswer:=False;
for k:=1 to i do begin
N:=Matr[k];
if (N.x*XResult+N.y*YResult<=N.b) then begin
{Если в ОДЗ}
c:=cTmp;
boolAnswer:=True;
end;
{далее проверяем вышла ли cTmp за ОДЗ}
if (N.x*XResult+N.y*YResult>N.b) then begin Exit
end;
end;
cTmp:=cTmp+STEP;{Увеличиваем cTmp на STEP}
if keyPressed then key:=ReadKey;{если Esc нажата, то прерываем}
until (key=#27) or (cTmp>=10000);
if boolAnswer then begin
{пишем ответ:}
{1. Рисуем целевую ф-ю в нужном месте}
c:=MainF.x*XResult+MainF.y*YResult;
MoveTo(MinX+1,MinY-Round(C/MainF.y*MASHT)-1);
SetColor(Red);{рисуем целевую линию на экр. красным}
LineTo(MinX+Round(C/MainF.x*MASHT)+1,MinY-1);
SetLineStyle(1,0,NormWidth);
SetColor(Yellow);
{2. Считаем max(f)}
Str(MainF.x*XResult+MainF.y*YResult:2:1,STmp);
Result:='max(f)='+Stmp;
{3. Рисуем значение на оси X}
Line(MinX+Round(XResult)*MASHT,MinY-Round(YResult)*MASHT,MinX+Round(XResult)*MASHT,MinY+3);
Str(XResult:2:1,STmp);
OutTextXY(MinX+Round(XResult)*MASHT,MinY+4,STmp);
Result:=Result+' при x='+Stmp;
{4. Рисуем значение на оси Y}
Line(MinX+Round(XResult)*MASHT,MinY-Round(YResult)*MASHT,MinX-3,MinY-Round(YResult)*MASHT);
Str(YResult:2:1,STmp);
OutTextXY(MinX-30,MinY-Round(YResult)*MASHT,STmp);
Result:=Result+' y='+Stmp;
SetColor(White);
SetLineStyle(0,0,NormWidth);
OutTextXY(300,230,Result);{Выводим строку ответа}
end
else
OutTextXY(7,3,'Вычисления не закончены!!!');
{Завешение программы}
Bar(0,0,GetMaxX,MaxY-1);
SetColor(White);
OutTextXY(7,3,'Нажмите любую клавишу для выхода');
ReadKey;
End;
BEGIN
i:=0;{Начальное значение кол-ва неравенств}
Gd:=Detect;
InitGraph(Gd, Gm, 'C:\BP\BGI'); { Путь к BGI драйверам }
if GraphResult <> grOk then Halt(1);
ShowXOY;
EnterNerav;
EnterMainF;
GetResult;
CloseGraph;
END.
Заключение
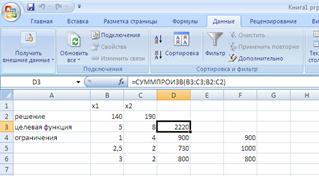
Программа решения задач линейного программирования графическим способом на IBM PC была написана на языке Borland Pascal 7.1. В ней, для удобства, рассматривается случай когда количество переменных равно двум т. е. решение задачи можно разместить на плоскости. С помощью этой программы можно наглядно продемонстрировать метод графического решения задач.
Вообще, с помощью графического метода может быть решена задача линейного программирования, система ограничений которой содержит n неизвестных и m линейно независимых уравнений, если N и M связаны соотношением N – M = 2.
Действительно, пусть поставлена задача линейного программирования.
Найти максимальное значение линейной функции
Z = С1х1+С2х2+... +СNxN
при ограничениях
a11x1 + a22x2 + ... + a1NХN = b1
a21x1 + a22x2 + ... + a2NХN = b2
. . . . . . . . . . . . . . .
aМ1x1 + aМ2x2 + ... + aМNХN = bМ
xj ≥ 0 (j = 1, 2, ..., N)
где все уравнения линейно независимы и выполняется cоотношение N - M = 2.
Используя метод Жордана-Гаусса, производим M исключений, в результате которых базисными неизвестными оказались, например, M первых неизвестных х1, х2, ..., хM, а свободными - два последних: хМ+1, и хN, т. е. система ограничений приняла вид:
x1 + a1,М+1xМ+1 + a1NХN = b1
x2 + a2,М+1xМ+1 + a2NХN = b2
. . . . . . . . . . . .
xМ + aМ, М+1x2 + aМNХN = bМ
xj ≥ 0 (j = 1, 2, ..., N)
С помощью уравнений преобразованной системы выражаем линейную функцию только через свободные неизвестные и, учитывая, что все базисные неизвестные - неотрицательные: хj ≥ 0 (j = 1, 2, ..., M), отбрасываем их, переходя к системе ограничений, выраженных в виде неравенств.
Литература
1. Абрамов Л.М., Капустин В.Ф. Математическое программирование. Л., Изд-Ленингр. ун-та, 1976. - 184 с.
2. Акулич И.Л. Математическое программирование в примерах и задачах: Учеб. пособие - 2-е изд., испр. и доп. - М.: Высш. шк. ,1993 - 336 с.
3. Ашманов С.А.Линейное программирование. - М.: Наука, 1981.
4. Баканов М.И., Шеремет А.Д. Теория экономического анализа: Учебник. -4-е изд., доп. и перераб. - М.: Финансы и статистика, 2000. - 416 с.
5. Баканов М.И., Шеремет А.Д.Экономический анализ: ситуации, тесты, примеры, задачи, выбор оптимальных решений, финансовое прогнозирование: Учеб. пособие. - М.: Финансы и статистика, 1999. -656 с.
6. Банди Б. Основы линейного программирования: Пер. с англ. - М.: Радио и связь, 1989. -176 с.
7. Габасов Р., Кириллова Ф.М. Методы линейного программирования. Ч.1. Общие задачи, Минск, Изд-во БГУ им. В.И. Ленина, 1977. - 176 с.
8. Габасов Р., Кириллова Ф.М. Методы линейного программирования. Ч.2. Транспортные задачи, Минск, Изд-во БГУ им. В.И. Ленина, 1977. - 240 с.
9. Глухов В.В., Медников М.Д., Коробко С.Б. Математические методы и модели для менеджмента - СПб.: Издательство “Лань”, 2000. -480 с.
10. Гольштейн Е.Г., Юдин Д.Б. Линейное программирование,теория, методы и приложения. - М.: Наука, 1969.
11. Гасс С.Линейное программирование. - М.: Физматгиз, 1961.
12. Заварыкин В. М. и др. Численные методы: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов / В.М. Заварыкин, В.Г. Житомирский, М.П. Лапчик. - М.: Просвещение, 1990. - 176 с
13. .Кузнецов А.В., Сакович В.А., Холод Н.И. Высшая математика. Математическое программирование. /Под общ. ред. проф. Кузнецова А.В., М., “ВЫШЭЙШАЯ ШКОЛА”, 1994. - 288 с.
14. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование: Учеб. пособие. – 2-е изд., перераб и доп. - М.: Высш. школа, 1980. -300 с.
15. Ляшенко И.Н, Карагодова Е.А, Черникова Н.В., Шор Н.З. Линейное и нелинейное программирование. Издательское объединение “Вища школа”, 1975. - 372 с.
16. Пер. с яп. /М. Кубонива, М. Табата, С. Табата, Ю. Хасэбэ, под ред. М. Кубонива. Математическая экономика на персональном компьютере: - М.: Высш. школа, 1980.
17. Под ред и с предисл. Е.З. Демиденко – М.: Финансы и статистика, 1991. – 304 с.
18. Солодовников А.С. Введение в линейную алгебру и линейное программирование. М., Изд. “Просвещение”, 1966. - 184 с.
19. Схрейвер А. Теория линейного и целочисленного программирования: В 2-х т. Т.1: Пер с англ. - М.: Мир, 1991. -360 с.
20. Тынкевич М.А. Экономико-математические методы (исследование операций). Изд. 2, испр. и доп. - Кемерово, 2000. - 177 с.
Рецензия
Похожие работы
... ячеек свидетельствует о том, что возможно лучшее решение и наоборот, если отрицательных ячеек нет, то было найдено оптимальное решение. 2. Содержательная постановка задачи Частным случаем задачи линейного программирования является транспортная задача. Проблема транспортировки включает поиск низко затратных схем распределения товарных запасов от многих источников до многих мест назначения ...
... игр, теория массового обслуживания, и др. 1. ПОСТАНОВКА ЗАДАЧИ Целью нашего курсового проекта является решение задачи линейного программирования графическим методом. 1.1 Математическое программирование. Математическое программирование ("планирование") – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ...
... с помощью двухэтапного метода, совпадает с решением, полученным в среде MS Excel с помощью программной надстройки «Поиск решения». 7. ПРИМЕРЫ ПОСТАНОВОК, ФОРМАЛИЗАЦИИ И РЕШЕНИЯ ПЕРСПЕКТИВНЫХ ОПТИМИЗАЦИОННЫХ УПРАВЛЕНЧЕСКИХ ЗАДАЧ Одним из методов решения задач линейного программирования является графический метод, применяемый для решения тех задач, в которых имеются только две переменные, ...
... ограничения несовместны, множество планов пусто и задача ЛП решения не имеет. Рис. 1.4 Рис. 1.5 Рис. 1.6 2. Симплекс-метод 2.1 Идея симплекс-метода Рассмотрим универсальный метод решения канонической задачи линейного программирования , , , с n переменными и m ограничениями-равенствами, известный как симплекс-метод. Множество планов канонической задачи – ...
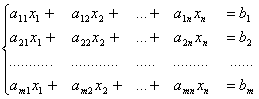
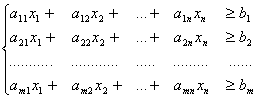
0 комментариев