Навигация
6 Да
7
нет
8 Да
9
нет
Лист
Кп-км-п-44-2203-99
10
11
12
13
Да
14
нет
15
16
Лист
Кп-км-п-44-2203-99
Блок-схема подпрограммы решения методом минимального элемента MINIELEM
1
2
3
4
5
6 Да
7
нет
8
Да
9
нет
Лист
Кп-км-п-44-2203-99
10
11
Да
12
13
Лист
Кп-км-п-44-2203-99
Блок-схема подпрограммы решения транспортной задачи Transsolver
1
2
Да
3
нет
4 Да
5
нет
6
7
нет
8
Лист
Кп-км-п-44-2203-99
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
Grids;
type
TForm1 = class(TForm)
StringGrid1: TStringGrid;
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
word:string;
words:TStringList;
i:integer;
implementation
{$R *.DFM}
Form1.slString=TStringList.Create;
for i:=1 to 8 do
begin
word:=IntTostr(i);
words.add(word)
end
end.
Лист
Кп-км-п-44-2203-99
unit TransTask;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,
StdCtrls, ExtCtrls, Grids, ComCtrls, Math;
type
TfmTransTask = class(TForm)
pgcTransTask: TPageControl;
tbsAbout: TTabSheet;
tbsData: TTabSheet;
tbsTarif: TTabSheet;
tbsSolve: TTabSheet;
Label1: TLabel;
edProviderCount: TEdit;
spnProviderCount: TUpDown;
Label2: TLabel;
stgProvider: TStringGrid;
Label3: TLabel;
Label4: TLabel;
edCustomerCount: TEdit;
spnCustomerCount: TUpDown;
stgCustomer: TStringGrid;
Label5: TLabel;
lblTypeTask: TLabel;
lblProviderGruz: TLabel;
lblCustomerGruz: TLabel;
stgTarif: TStringGrid;
stgSolve: TStringGrid;
rgMetod: TRadioGroup;
rbMinelem: TRadioButton;
rbFogel: TRadioButton;
rbTwoWall: TRadioButton;
btnSolve: TButton;
btnPrint: TButton;
Label6: TLabel;
Label7: TLabel;
Label8: TLabel;
Label9: TLabel;
btnLoadData: TButton;
btnLoadDataC: TButton;
lblProvider: TLabel;
lblCustomer: TLabel;
lblTupeTask: TLabel;
lblMsg: TLabel;
Label10: TLabel;
lblZ: TLabel;
procedure FormCreate(Sender: TObject);
procedure edProviderCountChange(Sender: TObject);
procedure edCustomerCountChange(Sender: TObject);
procedure btnLoadDataClick(Sender: TObject);
procedure btnLoadDataCClick(Sender: TObject);
procedure btnSolveClick(Sender: TObject);
procedure btnPrintClick(Sender: TObject);
Лист
Кп-км-п-44-2203-99
private{ Private declarations }
public
{ Public declarations }
end;
var
fmTransTask: TfmTransTask;
a,b: array of integer;// наличие груза у поставщиков
// и спрос у потребителей
c: array of array of integer; // матрица тарифов перевозок
d: array of array of integer;// матрица перевозок (решение)
z,m,n:integer; //число поставщиков и потребителей
s:string;
implementation
{$R *.DFM}
procedure ShowSolve;
var
i,j:integer;
begin
for i:= 0 to m-1 do
for j:= 0 to n-1 do
fmTransTask.stgSolve.Cells[j+1,i+1]:=IntToStr(d[i,j]);
fmTransTask.lblZ.Caption:=IntToStr(z);
end;
procedure Minelem;
label
l1;
var
i,j,imin,jmin,cmin:integer;
set_i:set of 0..255;
set_j:set of 0..255;
begin
// создаем множество индексов
set_i:=[];
for i:=0 to m-1 do include(set_i,i);
set_j:=[];
for j:=0 to n-1 do include(set_j,j);
z:=0;
repeat
// поиск первоначального минимального ьэлемента в матрице тарифов
for i:= 0 to m-1 do
for j:= 0 to n-1 do
if (i in set_i) and (j in set_j) then
begin
cmin:=c[i,j];
goto l1
end;
l1:
// поиск минимального элемента в
// в матрице тарифов c
for i:= 0 to m-1 do
for j:= 0 to n-1 do
if (i in set_i) and (j in set_j) then
if c[i,j]
Похожие работы
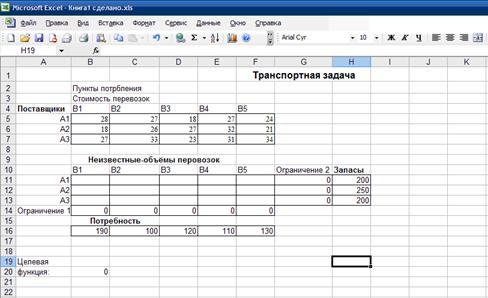
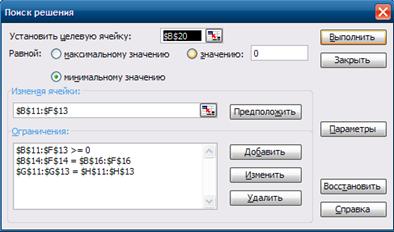
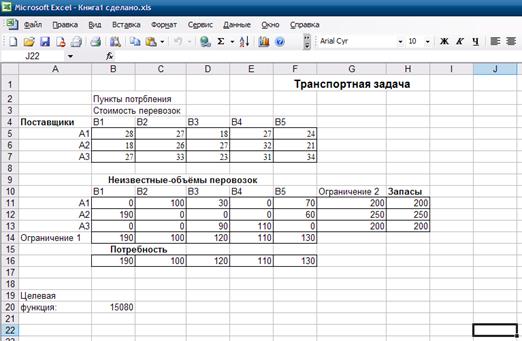
... F = 27*100 + 30*30 + 24*70 + 18*190 + 21*60 + 23*120 + 31*80 = 15110 Результат: Затраты на распределение товаров между магазинами найденные методом наименьшей стоимости составят 15110 рублей. 2.6 Применение возможностей электронных таблиц при решении транспортной задачи Для решения транспортной задачи также можно применять электронные таблицы (Microsoft Office Excel ). Для решения ...
... во многих экономических задачах, приводит к линейной функции с линейными ограничениями, наложенными на неизвестные. 2. Области применения и ограничения использования линейного программирования для решения экономических задач Особенно широкое применение методы и модели линейного программирования получили при решении задач экономии ресурсов (выбор ресурсосберегающих технологий, составление ...
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... получение которого связано с большим объемом вычислительных работ. Обычно рассмотренный метод используется при вычислениях с помощью ЭВМ. Как и для всякой задачи линейного программирования, оптимальный план транспортной задачи является и опорным планом. Для определения оптимального плана транспортной задачи можно использовать изложенные выше методы. Однако ввиду исключительной практической ...







0 комментариев