Навигация
Математическая постановка транспортной задачи линейного программирования
Содержание
Введение 2
1. Постановка задачи и ее математическая модель 3
2. Модели транспортной задачи 7
2.1. Закрытая модель транспортной задачи 7
2.2. Открытая модель транспортной задачи 8
3. Определение оптимального и опорного плана транспортной задачи 10
4. Методы определения первоначального опорного плана 12
4.1. Метод минимального элемента 12
4.2. Метод аппроксимации Фогеля 14
5. Методы определения оптимального плана 16
5.1. Венгерский метод 16
5.2. Метод потенциалов 17
Список использованной литературы 19
Введение
Транспортная задача линейного программирования получила в настоящее время широкое распространение в теоретических обработках и практическом применении на транспорте и в промышленности. Особенно важное значение она имеет в деле рационализации постановок важнейших видов промышленной и сельскохозяйственной продукции, а также оптимального планирования грузопотоков и работы различных видов транспорта.
Кроме того, к задачам транспортного типа сводятся многие другие задачи линейного программирования - задачи о назначениях, сетевые, календарного планирования.
Цель заданной работы - освоить математическую постановку транспортной задачи линейного программирования.
1. Постановка задачи и ее математическая модель
Транспортная задача является частным типом задачи линейного программирования и формулируется следующим образом. Имеется m пунктов отправления (или пунктов производства) Аi …, Аm, в которых сосредоточены запасы однородных продуктов в количестве a1, ..., аm единиц. Имеется n пунктов назначения (или пунктов потребления) В1, ..., Вm, потребность которых в указанных продуктах составляет b1, ..., bn единиц. Известны также транспортные расходы Сij, связанные с перевозкой единицы продукта из пункта Ai в пункт Вj, i ![]() 1, …, m; j
1, …, m; j ![]() 1, ..., n. Предположим, что
1, ..., n. Предположим, что
![]()
т. е. общий объем производства равен общему объему потребления. Требуется составить такой план перевозок (откуда, куда и сколько единиц продукта везти), чтобы удовлетворить спрос всех пунктов потребления за счет реализации всего продукта, произведенного всеми пунктами производства, при минимальной общей стоимости всех перевозок. Приведенная формулировка транспортной задачи называется замкнутой транспортной моделью. Формализуем эту задачу.
Пусть хij - количество единиц продукта, поставляемого из пункта Аi в пункт Вj. Подлежащие минимизации суммарные затраты на перевозку продуктов из всех пунктов производства во все пункты потребления выражаются формулой:
![]() (1)
(1)
Суммарное количество продукта, направляемого из каждого пункта отправления во все пункты назначения, должно быть равно запасу продукта в данном пункте. Формально это означает, что
![]() , i
, i ![]() 1, …, m (2)
1, …, m (2)
Суммарное количество груза, доставляемого в каждый пункт назначения из всех пунктов отправления, должно быть равно потребности. Это условие полного удовлетворения спроса:
![]() , j
, j ![]() 1, …, n (3)
1, …, n (3)
Объемы перевозок - неотрицательные числа, так как перевозки из пунктов потребления в пункты производства исключены:
xij![]() 0, i
0, i ![]() 1, ..., m; j
1, ..., m; j ![]() 1, ..., n (4)
1, ..., n (4)
Транспортная задача сводится, таким образом, к минимизации суммарных затрат при выполнении условий полного удовлетворения спроса и равенства вывозимого количества продукта запасам его в пунктах отправления.
Определение 1.
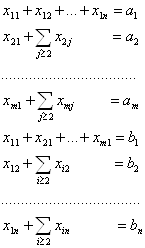
Всякое неотрицательное решение системы линейных уравнений
![]() , j
, j ![]() 1, …, n и
1, …, n и ![]() , i
, i ![]() 1, …, m,
1, …, m,
определяемое матрицей X=(xij)(i ![]() 1, …, m; j
1, …, m; j ![]() 1, ..., n), называется планом транспортной задачи.
1, ..., n), называется планом транспортной задачи.
Определение 2.
![]()
![]() План X*=(x*ij)(i
План X*=(x*ij)(i ![]() 1, …, m; j
1, …, m; j ![]() 1, ..., n), при котором функция
1, ..., n), при котором функция
![]()
принимает свое минимальное значение, называется оптимальным планом транспортной задачи.
Обычно исходные данные записываются в виде таблицы 1.
Таблица 1.
| Пункты отправления | Пункты назначения | Запасы | ||||
| В1 | … | Bj | … | Bn | А1 | |
| A1 | C11 X11 | … | C1j X1j | … | C1n X1n | a1 |
| … | … | … | … | … | … | … |
| Ai | Ci1 Xi1 | … | Cij Xij | … | Cin Xin | ai |
| … | … | … | … | … | … | … |
| Am | Cm1 Xm1 | … | Cmj Xmj | … | Cmn Xmn | am |
| Потребности | b1 | … | bj | … | bn | |
Очевидно, общее наличие груза у поставщиков равно ![]() , а общая потребность в грузе в пунктах назначения равна единице. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.
, а общая потребность в грузе в пунктах назначения равна единице. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.
![]() , (5)
, (5)
то модель такой транспортной задачи называется закрытой.
В ряде случаев не требуется, чтобы весь произведенный продукт в каждом пункте производства был реализован. В таких случаях баланс производства и потребления может быть нарушен:
![]() , i
, i ![]() 1, ..., m.
1, ..., m.
Введение этого условия приводит к открытой транспортной модели.
Теорема 1.
Любая транспортная задача, у которой суммарный объем запасов совпадает с суммарным объемом потребностей, имеет решение.
Похожие работы
... . При этом значения cij соответствуют коэффициентам целевой функции исходной замкнутой транспортной задачи (1) и в последующем не изменяются. Элементы xij соответствуют значениям переменных промежуточных решений транспортной задачи линейного программирования и изменяются на каждой итерации алгоритма. Если в некоторой ячейке xij=0, то такая ячейка называется свободной, если же xij>0, то такая ...
... , является линейной функцией переменных : (2.4) Требуется в области допустимых решений системы уравнений (2.1) и (2.1.1) найти решение, минимизирующее линейную функцию (2.4). Таким образом, мы видим, что транспортная задача является задачей линейного программирования. Для ее решения применяют также симплекс-метод, но в силу специфики задачи здесь можно обойтись без ...
... задачи линейного программирования, они очень сложны и решаются специальными, обычно многостадийными приемами с использованием эвристических элементов. 3. Решение задач 3.1. Решение задачи линейного программирования 3.1.1.Постановка задачи Сформулируем задачу: Определить значения переменных, обеспечивающие минимизацию целевой функции. Составим целевую функцию и зададим ограничения. ...
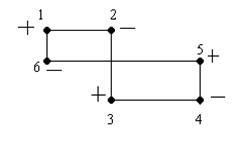
... . Система векторов условий транспортной задачи линейно независима тогда и только тогда, когда из соответствующих им клеток таблицы нельзя образовать ни одного цикла. Следовательно, допустимое решение транспортной задачи , i=1,2,…,m; j=1,2,…,n является опорным только в том случае, когда из занятых им клеток таблицы нельзя образовать ни одного цикла. Метод вычеркивания. Для проверки возможности ...





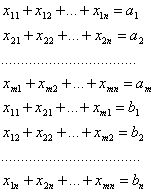



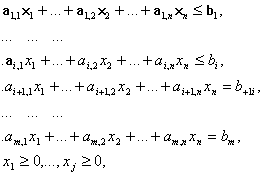
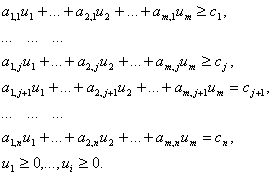
0 комментариев