Поиск в ширину на графах

Реферат В данной работе: 7 рисунков, 1 программа, 1 приложение, 35 листов.

Ключевые слова: граф, алгоритм, поиск, ширина, программа, аргумент, элемент, массив, очередь, память, время, сравнение.

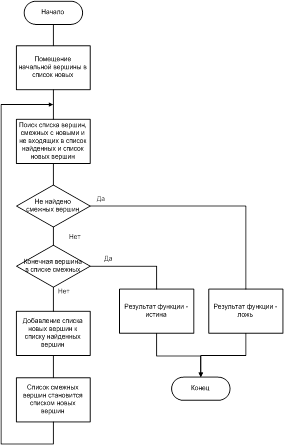
Цель работы: Исследовать эффективность алгоритма поиска в графе в ширину.

Результат работы программы: количество сравнений элемента с ключом поиска и время, за которое был найден элемент по данному алгоритму поиска.

Областью применение данного алгоритма может быть разнообразна, на пример при построении карт местности: вершины графа – города, связи – дороги.

Содержание Введение…………………………………………………………………..5 стр.

1.   Краткая теория………………………………………………………..6 стр.

2.   Анализ алгоритма……………………………………………………11 стр.

3.   Спецификация задачи……………………………………………….14 стр.

3.1 Входные и выходные данные…………………………………14 стр.

3.2 Используемые процедуры…………………………………….14 стр.

4.   Программа на языке Turbo Pascal..…………………………………15 стр.

4.1 Листинг программы…………..………….……………………15 стр.

4.2 Контрольный пример для тестирования №1….……………..26 стр.

4.3 Контрольный пример для тестирования №2….……………..26 стр.

4.4 Руководство пользователя…………………………………….27 стр.

5.   Результаты тестирования……………………………………………28 стр.

Заключение………………………………………………………………33 стр.

Список используемой литературы……………………………………..34 стр.

Приложение А…………………………………………………………….35 стр.

Введение.

Графы встречаются в сотнях разных задач, и алгоритмы обработки гра­фов очень важны.

Существует множество разработанных алгоритмов для решения различных задач из самых разных областей человеческой деятельности. Формулировка задачи описывает, каким требованиям должно удовлетворять решение задачи, а алгоритм, решающий эту задачу, находит объект, этим требованиям удовлетворяющий. ([1])

В этой работе, мы не будем давать четкого определения алгоритма, а попытаемся проанализировать и изучить алгоритм поиска в ширину в графе.

Поиском по заданному аргументу называется алгоритм, определяющий соответствие ключа с заданным аргументом. Алгоритм поиска в ширину может быть использован для просмотра созданного графа, чтобы узнать состав информационных вершин для последующего поиска.

В результате работы алгоритма поиска заданная вершина может быть найдена или может быть отмечено отсутствие ее в исходных данных.

Если заданная информационная вершина найдена, то происходит вывод об успешном окончании поиска, вывод времени поиска и времени поиска ключа.

1.   Краткая теория.

Очевидно, что наиболее понятный и полезный для человека способ представления графа — изображение графа на плоскости в виде точек и соединяющих их линий — будет совершенно бес­полезным, если мы захотим решать с помощью ЭВМ задачи, свя­занные с графами. Выбор соответствующей структуры данных для представления графов имеет принципиальное влияние на эффективность алгоритмов, поэтому мы подробнее остановимся на этой проблеме. Мы покажем несколько различных способов представления и кратко разберем их основные достоинства и не­достатки.

Мы будем рассматривать как ориентированные, так и нео­риентированные графы. Граф мы будем всегда обозначать G = (V,E), где V обозначает множество вершин, а Е — мно­жество ребер, причем Е Í V X V для ориентированного графа и ЕÍ{{х,у}: х,у Î V ۸ х¹у} для неориентированного графа. Будем также использовать обозначения |V| = n и |Е| = m.

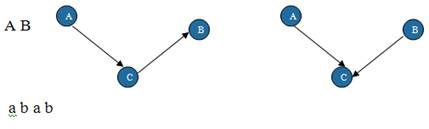
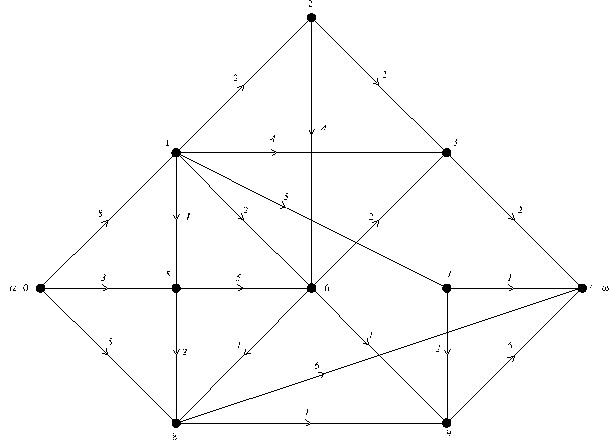
В теории графов классическим способом представления гра­фа служит матрица инциденций. Это матрица А с n строками, соответствующими вершинам, и m столбцами, соответствующими ребрам. Для ориентированного графа столбец, соответствующий дуге <x, y> Î E, содержит —1 в строке, соответствующей вер­шине х, 1 в строке, соответствующей вершине у, и нули во всех остальных строках (петлю, т. е. дугу вида <x, x>, удобно пред­ставлять иным значением в строке х, например, 2). В случае неориентированного графа столбец, соответствующий ребру {х,у}, содержит 1 в строках, соответствующих х и у, и нули в остальных строках. Это проиллюстрировано на рис. 2.1. С ал­горитмической точки зрения матрица инциденций является, ве­роятно, самым худшим способом представления графа, который только можно себе представить. Во-первых, он требует nm ячеек памяти, причем большинство этих ячеек вообще занято нулями. Неудобен также доступ к информации. Ответ на элементарные вопросы типа «существует ли дуга <x,y>?», «к каким вершинам ведут ребра из х?» требует в худшем случае перебора всех столб­цов матрицы, а следовательно, m шагов.

Лучшим способом представления графа является матрица смежности, определяемая как матрица В = [b•j] размера nхm,

<1,2>

<1,3>

<3,2>

<3,4>

<5,4>

<5,6>

<6,5>

(а) 1 –1 –1 0 0 0 0 0

2 1 0 1 0 0 0 0

3 0 1 -1 -1 0 0 0

4 0 0 0 1 1 0 0

 5 0 0 0 0 -1 -1 1

6 0 0 0 0 0 1 -1

 

{1,2}

{1,3}

{1,5}

{2,3}

{2,5}

{3,4}

{4,5}

{4,6}

{5,6}

(б) 1 1 1 1 0 0 0 0 0 0

2 1 0 0 1 1 0 0 0 0

 3 0 1 0 1 0 1 0 0 0

4 0 0 0 0 0 1 1 1 0

5 0 0 1 0 1 0 1 0 1

6 0 0 0 0 0 0 0 1 1

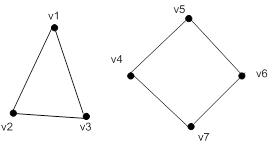
Рис. 1. а) Ориентированный граф и его матрица инциденций;

б) Неориенти­рованный граф и его матрица инциденций.

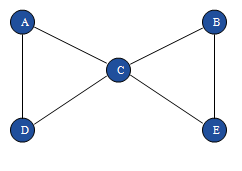
где b_ij = 1, если существует ребро, идущее из вершины х в вер­шину у, и b_ij = 0 в противном случае. Здесь мы подразумеваем, что ребро {х, у} неориентированного графа идет как от х к у, так и от у к х, так что матрица смежности такого графа всегда является симметричной. Это проиллюстрировано на рис. 2.

Основным преимуществом матрицы смежности является тот факт, что за один шаг можно получить ответ на вопрос «су­ществует ли ребро из х в y?». Недостатком же является тот факт, что независимо от числа ребер объем занятой памяти составляет n². На практике это неудобство можно иногда уменьшить, храня целую строку (столбец) матрицы в одном машинном слове — это возможно для малых n.

В качестве еще одного аргумента против использования матрицы смежности приведем теорему о числе шагов, которое

должен выполнить алгоритм, проверяющий на основе матрицы смежности некоторое свойство графа.

Пусть Р — некоторое свойство графа P(G) = 0 или P(G)=1 в зависимости от того, обладает или не обладает G на­шим свойством. Предположим, что свойство Р удовлетворяет следующим трем условиям:

(а) P(G)=P(G'), если графы G и G' изоморфны;

(б) P(G) = 0 для произвольного пустого графа <V,Æ> и P(G)=1 для произвольного полного графа <V, P₂(V)> с до­статочно большим числом вершин;

1 2 3 4 5 6 1 2 3 4 5 6

1 0 1 1 0 0 0 1 0 1 1 0 1 0

2 0 0 0 0 0 0 2 1 0 1 0 1 0

3 0 1 0 1 0 0 3 1 1 0 1 0 0

4 0 0 0 0 0 0 4 0 0 1 0 1 1

5 0 0 0 1 0 1 5 1 1 0 1 0 1

6 0 0 0 0 1 0 6 0 0 0 1 1 0

 

Рис. 2. Матрицы инциденций для графов на рис.1.

(в) добавление ребра не нарушает свойства Р, т. е. P(G)<P(G') для произвольных графов G=(F,E) и G'=(V, E'), таких что Е = Е'.

Примером такого свойства Р является существование цикла (в графе, имеющем, по крайней мере три вершины).

Теорема . Если Р — свойство графа, отвечающее условиям (а), (б), (в), то каждый алгоритм, проверяющий свойство Р (т. е. вычисляющий значение P(G) для данного графа G) на основе матрицы смежности, выполняет в худшем случае Ω(n²) шагов, где n — число вершин графа.

Эта теорема справедлива также для ориентированных гра­фов и для свойств, не зависящих от петель графа, т, е. отве­чающих дополнительному условию

(г) P(G) = P(G') для произвольных ориентированных гра­фов G = < V, E>, G’ = < V, Е> U <v, v>>, v C V.

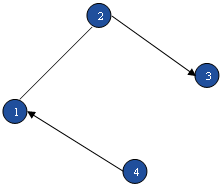
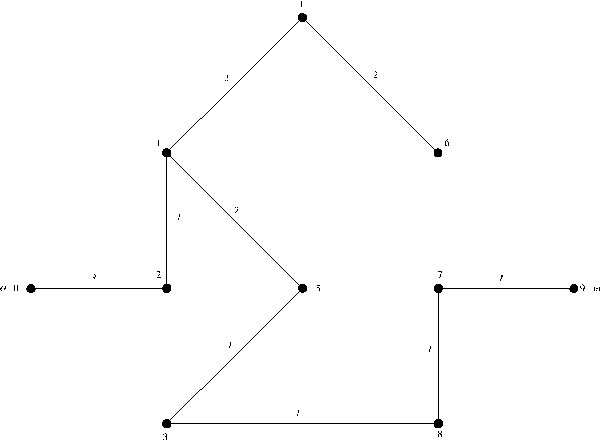
Более экономным в отношении памяти (особенно в случае, неплотных графов, когда m гораздо меньше n2) является ме­тод представления графа с помощью списка пар, соответствующих его ребрам. Пара <x, у> соответствует дуге <х, у>, если граф ориентированный, и ребру {х, y} в случае неориентиро­ванного графа(рис. 3). Очевидно, что объем памяти в этом случае составляет 2т. Неудобством является большое число шагов — порядка т в худшем случае, — необходимое для по­лучения множества вершин, к которым ведут ребра из данной вершины.

Ситуацию можно значительно улучшить, упорядочив мно­жество пар лексикографически и применяя двоичный поиск, но лучшим решением во многих случаях оказывается структура

1	2
1	3
1	5
2	3
2	5
3	4
4	5
4	6
5	6

1	2
1	3
3	2
3	4
5	4
5	6
6	5

Рис.3. Списки ребер соответствующие графам на рис.1.

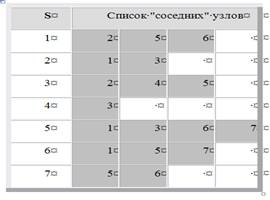
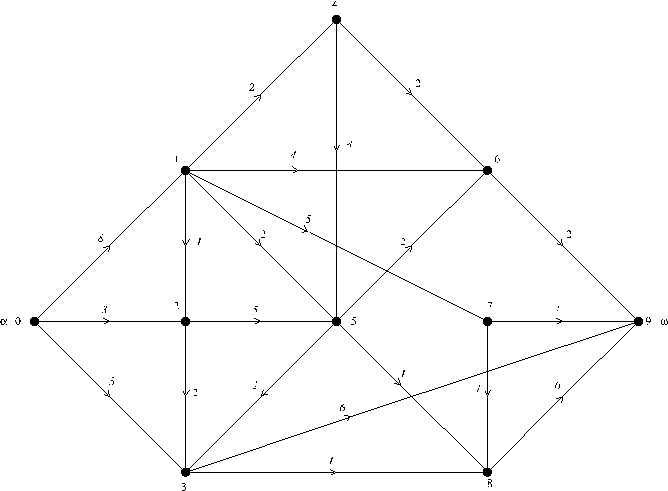
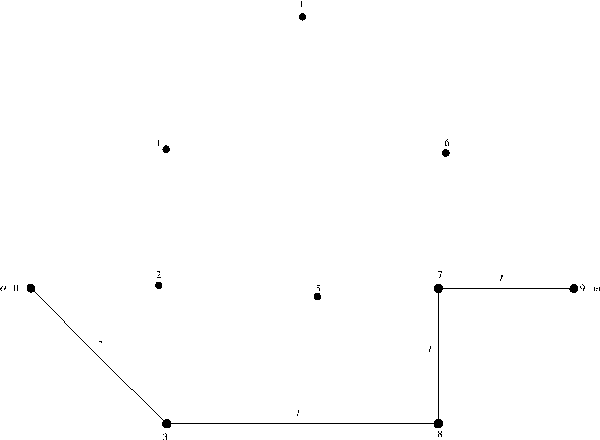
данных, которую мы будем называть списками инцидентности. Она содержит для каждой вершины v C V список вершин и, таких что v -> u (или v — ив случае неориентированного гра­фа). Точнее, каждый элемент такого списка является записью г, содержащей вершину г. строка и указатель г. след на сле­дующую запись в списке (г. след = nil для последней записи в списке). Начало каждого списка хранится в таблице НАЧАЛО; точнее, HAЧАЛО[v] является указателем на начало спи­ска, содержащего вершины из множества {u: v+u} ({u: v - u} для неориентированного графа). Весь такой список обычно не­формально будем обозначать 3AПИСЬ[v], а цикл, выполняю­щий определенную операцию для каждого элемента и из этого списка в произвольной, но четко установленной последователь­ности, соответствующей очередности элементов в списке, будем записывать «for u C ЗАПИСЬ [v] do ...».

Отметим, что для неориентированных графов каждое ребро {u, v} представлено дважды: через вершину v в списке ЗАПИСЬ[u] и через вершину и в списке ЗАПИСЬ[v]. Во многих алгоритмах структура графа динамически модифицируется добавлением и удалением ребер. В таких случаях полагаем, что в наших списках инцидентности элемент списка ЗАПИСЬ [u], содержащий вершину и, снабжен указателем на элемент спи­ска 3AПИCЬ[v], содержащий вершину и, и что каждый эле­мент списка содержит указатель не только к следующему эле­менту, но и к предыдущему. Тогда удаляя некоторый элемент

	(б)

Рис.4. Списки инцидентности ЗПИСЬ[v], v =V, соответствующие графам на рис.1.

из списка, мы можем легко за число шагов, ограниченное кон­стантой, удалить другой элемент, представляющий то же са­мое ребро, не просматривая список, содержащий этот элемент.

Аналогичным способом определяем для каждой вершины и неориентированного графа список ПРЕДШ[v], содержащий вершины из множества (u: u -> v).

Число ячеек памяти, необходимое для представления графа с помощью списков инцидентности, будет, очевидно, иметь по­рядок m + n. На рис.4 представлены списки инцидентности, соответствующие графам на рис. 1.