Навигация
2. Анализ алгоритма.
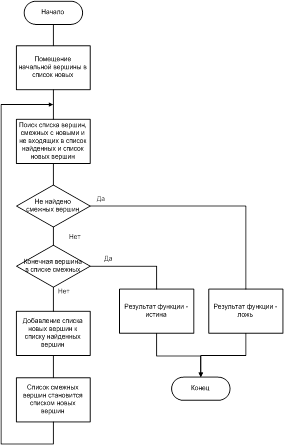
Рассмотрим метод поиска в графе, называемый поиском в ширину (англ: breadth first search). Прежде чем описать его, отметим, что при поиске в глубину чем позднее будет посещена вершина, тем раньше она будет использована — точнее, так будет при допущении, что вторая вершина посещается перед использованием первой. Это прямое следствие того факта, что просмотренные, но еще не использованные вершины скапливаются в стеке. Поиск в ширину, грубо говоря, основывается на замене стека очередью. После такой модификации, чем раньше посещается вершина (помещается в очередь), тем раньше она используется (удаляется из очереди). Использование вершины происходит с помощью просмотра сразу всех еще не просмотренных соседей этой вершины. Вся процедура поиска представлена ниже (данная процедура используется также и для просмотра графа, и в псевдокоде, описанном ниже, отсутствуют операторы, которые не используются для поиска).
1 procedure WS (v);
(*поиск в ширину в графе с началом в вершине v;
переменные НОВЫЙ, ЗАПИСЬ — глобальные *)
2 begin
3 ОЧЕРЕДЬ := Æ; ОЧЕРЕДЬ <= v; НОВЫЙ [v] := ложь
4 while ОЧЕРЕДЬ ¹ Æ do
5 begin р<= ОЧЕРЕДЬ; посетить р;
6 for u Î ЗАПИСЬ [р] do
7 if НОВЫЙ [u] then
8 begin ОЧЕРЕДЬ <= u; НОВЫЙ [u]:=ложь
9 end
10 end
11 end
Примечание: в 7-й строке псевдокода кроме условия НОВЫЙ[u] должно также выполниться условие наличия связи (ребра) между v-й и u-й вершинами. Для установки наличия ребра сначала в списке v-й вершины ищется информационное значение и-й вершины. Если оно найдено, то ребро установлено, если нет, то информационное значение v-й вершины ищется в списке и-й вершины, т.е. наоборот. В результате добавления двух лишних циклов поиска общий алгоритм поиска несколько теряет компактность, но на быстродействии в целом это не сказывается.
1 procedure Write_S;
2 begin
3 for v Î V do НОВЫЙ[u]:= истина; (* инициализация *)
4 for v Î V do
5 if HOBЫЙ[v] then WG(v)
6 end
Способом, аналогичным тому, какой был применен для поиска в глубину, можно легко показать, что вызов процедуры WS(v) приводит к посещению всех вершин связной компоненты графа, содержащей вершину v, причем каждая вершина просматривается в точности один раз. Вычислительная сложность поиска в ширину также имеет порядок О(m + n), так как каждая вершина помещается в очередь и удаляется из очереди в точности один раз, а число итераций цикла 6, очевидно, будет иметь порядок числа ребер графа.
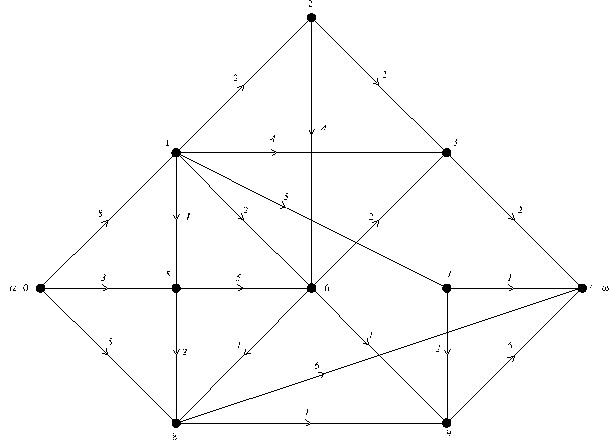
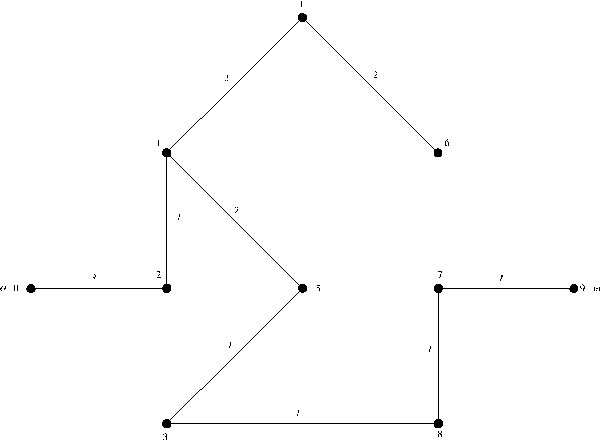
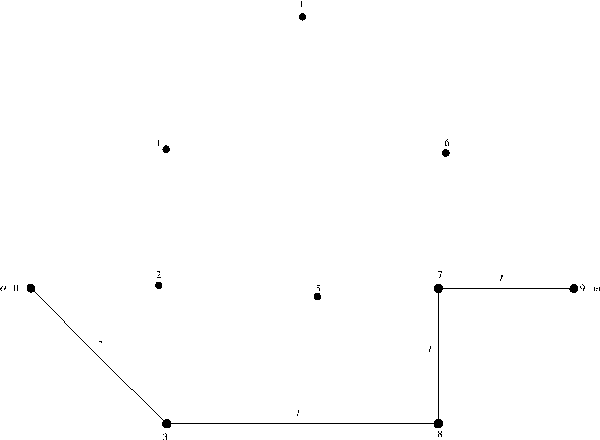
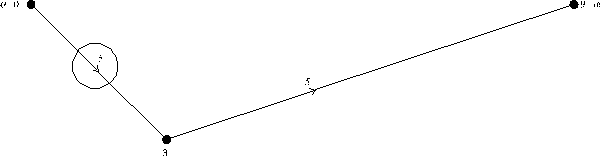
В очереди помещены сначала вершины, находящиеся на расстоянии 0 от v (т. е. сама вершина v), затем поочередно все новые вершины, достижимые из v, т. е. вершины, находящиеся на расстоянии 1 от v, и т. д. Под расстоянием здесь мы понимаем длину кратчайшего пути. Предположим теперь, что мы уже рассмотрели все вершины, находящиеся на расстоянии, не превосходящем r, от v, что очередь содержит все вершины, находящиеся от v на расстоянии r, и только эти вершины. Использовав каждую вершину р, находящуюся в очереди, наша процедура просматривает некоторые новые вершины, и каждая такая новая вершина u находится, очевидно, на расстоянии г + 1 от v. После использования всех вершин из очереди, находящихся на расстоянии r от v, она (очередь), очевидно, содержит множество вершин, находящихся на расстоянии r + 1 от v, и легко заметить, что условие индукции выполняется и для расстояния r + 1.
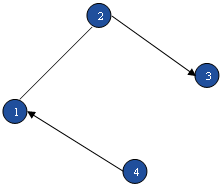
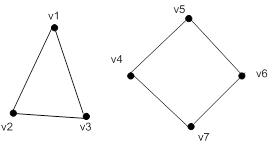
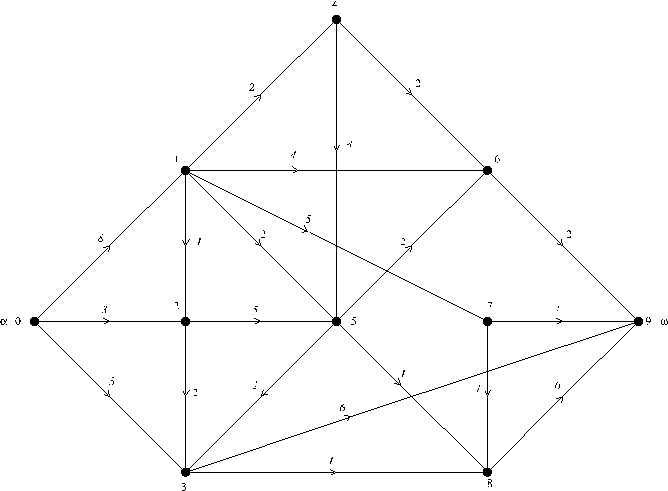
На рис. 5 представлен граф, вершины которого занумерованы согласно очередности, в которой они посещаются в процессе поиска в глубину.
Как и в случае поиска в глубину, процедуру WS можно использовать без всяких модификаций и тогда, когда списки
| |||
Рис. 5 Нумерация вершин графа (в скобках), соответствующая очередности, в которой они просматриваются в процессе поиска в ширину.
инцидентности ЗАПИСЬ[v], v = V, определяют некоторый ориентированный граф. Очевидно, что тогда посещаются только те вершины, до которых существует путь от вершины, с которой мы начинаем поиск
3. Спецификация задачи
3.1 Входные и выходные данные
ver – массив вершин графа, заполняемый случайным образом целыми числами в диапазоне от 0 до 1000;
nv - массив флагов проверки вершин;
ocher – массив для организации очереди, заполняемой значениями рассматриваемых информационных вершин графа;
raz – переменная целочисленного типа, определяющая в программе размер создаваемого графа;
schet – счетчик количества сравнений в процедуре поиска;
key – вводимый с клавиатуры ключ поиска;
mgsi – переменная логического типа, разрешающая вывод списка инцидентности графа;
prosm - переменная логического типа, превращающая процедуру поиска WS в процедуру просмотра графа;
find - переменная логического типа, определяемая при нахождении искомой информационной вершины;
craz, menu, mg, sormen – переменные символьного типа для работы с меню программы.
Похожие работы
... . 4.1 Требования к представлению графов Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Далее приведены четыре наиболее часто используемых представления с указанием характеристики п(р, q) — объема памяти для ...
... к другой. Граф является связным, если все вершины связаны между собой. Можно утверждать, что граф является связным, если одну из вершин можно соединить со всеми другими путем. Алгоритм определения связности графа заключается в поиске пути от первой вершины ко всем остальным. Если все пути можно найти – значит граф связный. Поиск пути от одной вершины к другой будет выполняться по алгоритму ...
... не соединенными ребрами вершинами – на графе из двух вершин, соединенных ребром – на сложном графе Стратегия тестирования Сперва, с помощью определения понятия "клика", были найдены клики данного графа, после чего результаты сравнивались с результатом работы программы. 1. Тестирование на пустом графе. Теоретические расчеты: поскольку граф пуст (множество его вершин есть пустое множество) ...
... vij матрицы весов. Используя венгерский алгоритм, найти совершенное паросочетание минимального (максимального веса). Выполнить рисунок. Матрица весов двудольного графа K55 : y1 y2 y3 y4 y5 x1 2 0 0 0 0 x2 0 7 9 8 6 x3 0 1 3 2 2 x4 0 8 7 6 4 x5 0 7 6 8 3 Первый этап - получение нулей не нужен, т. к. нули уже есть во всех строк и столбцах. Второй этап - ...

0 комментариев