Навигация
Команда IRET извлекает из стека адрес возврата - IP,CS и содержимое PSW;
8. Команда IRET извлекает из стека адрес возврата - IP,CS и содержимое PSW;
9. МП прдолжает работу с адреса возврата. При выполнении программных прерываний по команде INT N действия выполняются с п.3. N находится в пределах 0 <= N <= 255, поэтому четырехбайтовые вектора прерываний занимают первые 1024 байта памяти.
8.7.3 ПРЯМОЙ ДОСТУП К ПАМЯТИ (ПДП) И ТРАНЗАКЦИИОбмен большим количеством байтов, между ВУ (например дисковым накопителем) и памятью с помощью предыдущих двух методов малоэффективен, т.к. обмен происходит по цепочке: ВУ - аккумулятор (AX или AL) - память или наоборот. В режиме ПДП при поступлении запроса от ВУ на вход HOLD, МП разрешает обмен выходным сигналом HLDA. Микропроцессор на время обмена отключается от ШУ,ШД и ША переводя их в третье состояние по входам ~OE буферных элементов сигналом ~BUSEN = 1 .Специальная микросхема (контроллер ПДП) использует освободившиеся шины для высокоскоростного прямого обмена ВУ - память. Скорость обмена достигает многих мегабит/сек.
На рис.6 показан процесс выполнения основной (фоновой) программы - интервалы времени (начало..t1, t2..конец) и выполнение процедуры передачи массива данных, на рисунке этот отрезок времени обозначен двойной линией. На диаграмме (А) ЭВМ задействована только для передачи (отрезок t1..t2), в остальное время компьютер бездействует. Во втором варианте - диаграмма (Б), код программы передачи жестко встроен в фоновую задачу. В третьем варианте (В) передача массива оформлена в виде подпрограммы прерывания, причем если запроса на прерывание не поступит,то суммарное время на выполнение фоновой программы уменьшится на t2-t1. При использовании режима ПДП сохраняются преимущества метода прерывания, время на передачу сокращается - диаграмма (Г), но фоновая задача по прежнему прерывается. В последнем случае передача данных производится почти без нарушения хода программы параллельно во времени (Д). Транзакции реализованы в некоторых семействах однокристальных микроЭВМ например в MCS-96.
ЗАДАЧИ И УПРАЖНЕНИЯОдна подпрограмма вызывает другую.Укажите короткий адрес возврата из вложенной прoцедуры.
Пояснение : Вложенная подпрограмма это подпрограмма, которая вызывается из другой подпрограммы. Вызов подпрограммы сопровождается помещением в стек адреса возврата. Стек заполняется начиная с дна. Короткий адрес - двухбайтовый адрес в пределах одного кодового сегмента. Байты в стек помещаются по правилу "старший байт по старшему адресу". Теперь нетрудно ответить на предложенный вопрос: 4dba.
В тексте программы следуют подряд команды: PUSH AX; PUSH CX; POP DX; POP BX. Чему будет равно содержимое регистра BH? Рисунок стека соответствует промежуточному состоянию (до выполнения команд POP).
Пояснение : В стек дважды что-то помещается и дважды что-то извлекается, причем последние два байта помещаются в регистр BX. Перефразируя правило "последним вошел - первым вышел" в "последним вышел - первым вошел", придем к выводу, что содержимое AX засылается в регистр BX. Команда PUSH AX помещает два байта в стек по правилу "старшая половина двухбайтового регистра - по старшему адресу". Ответ: c9
В тексте программы следуют подряд команды: POP AX; POP DX. Чему будет равно содержимое регистра DL?
Ответ: 4c
На временных диаграммах внизу приведены управляющие сигналы на выходах микропроцессора (без сохpанения точных вpеменных пpопоpций). Что осуществляется в момент времени отмеченный знаком + ? Чтение данных из памяти, запись данных в память вывод данных в порт, ввод данных из порта, ничего из указанного выше.
Пояснения : Если ~DEN=0 (разрешение данных) возможно 4 случая (для приведенных диаграмм): 1) M/~IO = 0, ~RD = 0 активны сигналы ввод/вывод (~IO) и чтение-ввод (~RD). 2) M/~IO = 0, ~WR = 0 активны сигналы ввод/вывод (~IO) и запись-вывод(~WR). 3) M/~IO = 1, ~RD = 0 активны сигналы обращения к памяти(M) и чтение-ввод(~RD). 4) M/~IO = 1, ~WR = 0 активны сигналы обращения к памяти(M) и запись-вывод(~WR).
Ответ: Вывод данных в порт.
Приложение № 3 ОСНОВНЫЕ ПОЛОЖЕНИЯ АЛГЕБРЫ ЛОГИКИВ отличие от аналоговых электронных устройств, в цифровых устройствах (ЦУ) входные и выходные сигналы могут принимать ограниченное количество состояний. В соответствии с логическим соглашением (ГОСТ 2.743-82), в зависимости от конкретной физической реализации элементов ЦУ, более положительному значению физической величины, "H" - уровень, соответствует состояние "логическая 1", а менее положительному значению ,"L - уровень" - "логический 0". Такое соглашение называется положительной логикой. Обратное соотношение называется отрицательной логикой. В ГОСТ'е 19480 - 89 даны наименования, определения и условные обозначения основных параметров и характеристик цифровых микросхем.
Теоретической основой проектирования ЦУ является алгебра-логики или булева алгебра, оперирующая логическими переменными. Для логических переменных, принимающих только два значения,существуют 4 основных операции. Операция логическое "И" (AND) конъюнкция или логическое умножение, обозначается * или /\. Операция логическое "ИЛИ" (OR), дизъюнкция или логическое сложение, обозначается + или \/ . Операция логическое "НЕ" (NOT), изменение значения, инверсия или отрицание, обозначается чертой над логическим выражением. Инверсия иногда будет в тексте обозначаться знаком " ~ ". Операция эквивалентности обозначается "=" . Следующие соотношения являются аксиомами.
| (1) | 0 + 0 = 0 | 1 * 1 = 1 | (1') | |
| (2) | 1 + 1 = 1 | 0 * 0 = 0 | (2') | |
| (3) | 1 + 0 = 0 + 1 = 1 | 0 * 1 = 1 * 0 = 0 | (3') | |
| (4) | ~1 = 0 | ~0 = 1 | (4') |
Из (1, 2) и (1',2') следует: x + x = x и x * x = x. (5)
Из (1, 3) и (2',3') следует: x + 0 = x и 0 * x = 0. (6)
Из (2, 3) и (1',3') следует: 1 + x = 1 и x * 1 = x. (7)
Из (3) и (3') следует: x +~x = 1 и~x * x = 0. (8)
Из (4) и (4') следует: ~(~x) = x. (9)
И, наконец, из (1,1'), (2,2'), (3,3') и (4,4') следует:
~( x0+x1 ) = ~x0 * ~x1 и ~( x0 * x1) = ~x0 + ~x1 . (10)
Последние выражения (10) называют принципом двойственности или теоремой Де Моргана (инверсия логической суммы равна логическому произведению инверсий и наоборот). Соотношения двойственности для n переменных, часто записывают в виде:
~(x1 + .. + xn) = ~x1 * . .* ~xn и
~(x1 * .. * xn) = ~x1 + .. + ~xn (11)
На функции И и ИЛИ распространяются обычные алгебраические законы - переместительный, сочетательный и распределительный, которые легко доказываются методом перебора: x1 op x0 = x0 op x1 - переместительный, x2 op x1 op x0 = (x2 op x1) op x0 - сочетательный и x2*(x1+x0) = (x2*x1) + (x2*x0) и x2 + (x1*x0) = (x2+x1) * (x2+x0) - распределительный, где операция op может быть, либо И, либо ИЛИ. Наряду с тремя основными логическими функциями, называемыми также переключательными, существуют и другие.
1.2 ПЕРЕКЛЮЧАТЕЛЬНЫЕ ФУНКЦИИДля n - логических переменных (аргументов) существует 2n их комбинаций или двоичных наборов. На каждом таком наборе может быть определено значение функции 0 или 1. Если значения функции отличаются хотя бы на одном наборе, функции - разные. Общее число переключательных функций (ПФ) от n аргументов равно N=22n. Для n=2, N=16. При n=3, N=256 и далее очень быстро растет. Практическое значение имеют 16 функций от 2-х переменных, т.к. любое сложное выражение можно рассматривать как композицию из простейших. В таблице 1 приведены некоторые из ПФ для n=2. i-номер набора входных переменных x1 и x0.
ЗАПОМНИТЕ СЛЕДУЮЩИЕ ОПРЕДЕЛЕНИЯ. Функция "И" равна единице, если равны единице ВСЕ ее аргументы. Функция "ИЛИ" равна единице, если равен единице ХОТЯ БЫ один аргумент. Функция "ИСКЛЮЧАЮЩЕЕ ИЛИ" (XOR) равна единице, если равен единице ТОЛЬКО один ее аргумент.
1.3 УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ НА СХЕМАХКоличество входов логического элемента, участвующих в формировании логической функции, называется коэффициентом объединения - Коб ( не путать с коэффициентом разветвления). У всех выше приведенных схем, за исключением инвертора, коэффициент объединения равен двум. Промышленностью выпускаются схемы с Коб=2,3,4,8. Для получения схем с другим числом входов основные элементы можно объединять. Например, если требуется пятивходовая схема И, то ее можно получить, используя сочетательный закон следующим способом: x0 * x1 * x2 * x3 * x4 = (x0*x1) * (x2*x3*x4) = (x0*x1) * x2 * x3 * x4, т.е. требуются две двухвходовые и одна трехвходовая схемы И, для первого варианта, либо одна двухвходовая и одна четырехвходовая - для второго (рис.1).
Можно использовать и восьмивходовую схему И, подав на незадействованные входы "1", либо некоторые из переменных, в соответствии с выражениями (5) или (7).
1.4 СПОСОБЫ ПРЕДСТАВЛЕНИЯ ЛОГИЧЕСКИХ ФУНКЦИЙЦелью проектирования цифрового устройства является получение его логической функции (ЛФ) и соответствующей ей схемной реализации. ЛФ могут иметь различные формы представления: 1) словесное, 2) графическое, 3) табличное, 4) алгебраическое, 5) на алгоритмическом языке (например VHDL) и 6) схемное. В качестве примера, рассмотрим функцию Y от двух переменных x1 и x0, заданную словесным описанием: Y=1, если переменные НЕ РАВНЫ и Y=0, если x1=x0. Такую ЛФ удобно назвать функцией НЕРАВНОЗНАЧНОСТИ. Переходим к табличному представлению Y (таблица 2).
Табличное представление значений ЛФ для всех наборов входных переменных называется таблицей истинности. В общем виде переход от табличного представления к алгебраическому может осуществляться по формуле (12), одной из основных в алгебре логики.
Выражение (12) называется совершенной дизъюнктивной нормальной формой ЛФ (СДНФ). mi - минтерм или логическое произведение всех переменных i-го двоичного набора, входящих в прямом виде, если значение этой переменной в наборе равно 1, и в инверсном виде, если ее значение равно 0. fi - значение ЛФ на i - ом наборе. Доказательство (12) базируется на теореме разложения, в соответствии с которой любую ЛФ f(..) от n-переменных можно разложить по переменной xi в виде: f(x(n-1),...,xi,. ..,x0) = ~xi*f(x(n-1),...,0,..,x0) + xi*f(x(n-1),..,1,..,x0). Это выражение для xi=0 равно ~0*f(x(n-1),...,0,..,x0) + 0*f(x(n-1),..,1,..,x0) = f(x(n-1),...,0,..,x0). При xi=1 оно будет равно ~1*f(x(n-1),..,1,..,x0) + 1*f(x(n-1),..,1,..,x0) = f(x(n-1),...,1,..,x0), т.е. при любых значениях xi теорема разложения справедлива. Теорему разложения можно применить n раз и тогда ЛФ будет разложена по всем своим переменным.
В виде примера рассмотрим функцию F=f(x1,x0) от двух переменных. Разложение этой функции по переменной x1 даст: F= ~x1*f(0,x0) + x1*f(1,x0) . Продолжая эту операцию для переменной x0, получим:
F =~x1*(~x0*(f(0,0) + x0*(f(0,1)) + x1*(~x0*(f(1,0) + x0*(f(1,1)) = ~x1*~x0*f(0,0) + ~x1*x0*f(0,1) + x1*~x0*f(1,0) + x1*x0*f(1,1). (12.1)
Выражение (12.1) позволяет записать все переключательные функции от двух переменных, используя только три основных логических операции.
Рассмотрим разложение функций F7-"ИЛИ" и F1-"И", для чего необходимо обратиться к соответствующим строчкам таблицы 1. Функция И на двоичных наборах входных переменных x1 и x0 (00,01,10,11) принимает значения 0,0,0,1. Записывая выражение (12.1) для этих значений получим: F1(x1,x0 ) = ~x1*~x0*0 + ~x1*x0*0 + x1*~x0*0 + x1*x0*1 = x1*x0, что соогласуется с ее определением. Таким же образом, находим алгебраическое выражение функции F7-"ИЛИ", которая, соответственно, на тех же входных наборах принимает значения: 0,1,1,1. Тогда, в соответствии с (12.1), F7(x1,x0) = ~x1*~x0*0 + ~x1*x0*1 + x1*~x0*1 + x1*x0*1. Вынося за скобки в двух последних слагаемых x1, получим F7 = ~x1*x0*1 + x1*(~x0*1 + x0*1). На основании аксиомы (8), выражение в скобке равно "1" и F7 = ~x1*x0*1 + x1. Применяя распределительный закон, найдем (~x1+x1) * (x0+x1) = x1+x0.
Возвращаясь к таблице 2, получим Y = 0*~x1*~x0 + 1*~x1*x0 + 1*x1*~x0 + 0*x1*x0 = ~x1*x0 + x1*~x0 = x1 (+) x0 = F6 (функцияия неравнозначности).
С помощью формулы (12) любую, сколь угодно сложную, логическую функцию можно представить в виде трех основных ЛФ: "И", "ИЛИ", "НЕ", представляющих собой логический базис.
1.5 ЛОГИЧЕСКИЙ БАЗИСНабор простейших ЛФ, позволяющих реализовать любую другую функцию называется логическим базисом (ЛБ). Функции И, ИЛИ, НЕ не являются минимальным ЛБ, т.к. сами могут быть представлены через другие функции, например через F8(ИЛИ -НЕ) или F14(И - НЕ).
Следовательно базис "И - НЕ" является минимальным. Реализацию НЕ,И,ИЛИ в базисе "ИЛИ - НЕ" произвести самостоятельно, используя перечисленные аксиомы.
1.6 СХЕМНЫЕ ОСОБЕННОСТИ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВПриведенные выше логические элементы (ЛЭ) И, ИЛИ, НЕ, И-НЕ и другие могут иметь некоторые схемотехнические особенности.
Похожие работы
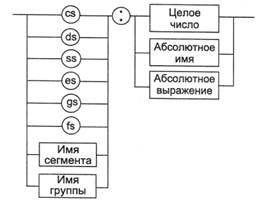
... как единое целое. Результатом вычисления выражения может быть адрес некоторой ячейки памяти или некоторое константное (абсолютное) значение. В табл. 2.2 приведены поддерживаемые языком ассемблера операторы и перечислены их приоритеты. Арифметические операторы. К ним относятся унарные операторы «+» и «-», бинарные «+» и «-», операторы умножения «*», целочисленного деления «/», получения остатка ...
... ) ФАКУЛЬТЕТ ЭЛЕКТРОНИКИ И ПРИБОРОСТРОЕНИЯ КАФЕДРА КЭС группа Э-92 ДАТА ЗАЩИТЫ апреля 1997 г. Отзыв на дипломную работу студента гр.Э-92 Сорокина Ю.В. “Разработка программы контроллера автоматически связываемых объектов для управления конструкторской документацией в среде Windows 95/NT”. Широкое использование вычислительной техники в народном хозяйстве требует увеличения производства и ...
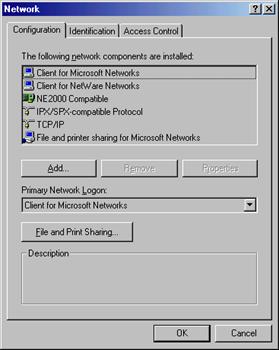
... выбрать имя в ListBox’e и нажать кнопку «OK», после чего выбранное имя автоматически отобразиться в окне получателя сообщения. Рис. 1.10. Выбор адресата получателя Поиск компьютеров в локальной сети Приведём пример кода программы, реализующую поиск компьютеров в локальной сети Microsoft. procedure TForm4. Button1Click (Sender: TObject); var Q, BufferSize: DWord; R: THandle; Buf: ^ ...
... значения низкого порога температуры, высвечивается сообщение и остается до пор, пока температура не станет выше, сохраненного значения низкого порога температуры. 3. Разработка программы Для того чтобы нам реализовать программу, необходимо компьютером считывать сигналы. Считывать сигналы будем с помощью параллельного порта LPT1. Pin In/Out Signal Name Pin In/Out Signal ...
0 комментариев