Навигация
5. Контрольный пример
Данный метод протестирован на контрольном примере и реализован с помощью языка программирования С++.
В результате вычислений контрольного примера вида y’=2x+y с интервалом [0,1],
количеством шагов равному 5 и начальным условием у равным 1, с помощью программы, получились следующие результаты:
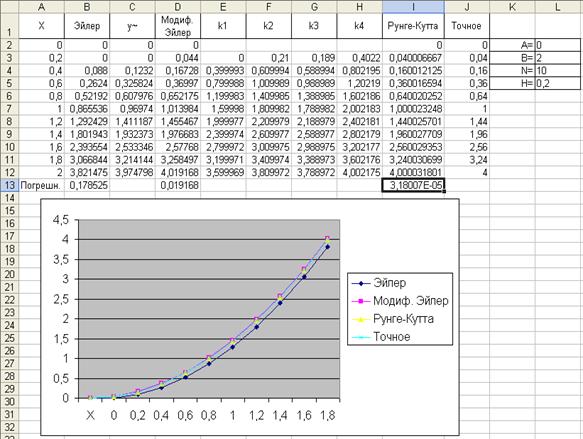
Рис. 2. Экран с результатами выполнения программы.
Как видно, при вычислении программа на первом шаге берёт начальные значения для вычисления, а на последующих берёт значения полученные с предыдущих шагов. Можно сделать вывод, что точность вычисления данного метода зависит от количества выбранных шагов: чем больше шагов, тем меньше фиксированное приращение , а следовательно она более точно вычисляет значение всего интервала.
По работе программы стало видно, что с её использованием намного упростилась работа пользователя. Пользователь просто вводит интервал на котором должен вычисляться пример, количество шагов и начальное значения и программа выдаёт уже готовое решение данного примера.
6.Анализ полученных результатов.
По результатам программы можно составить таблицу сравнения результатов полученных при использовании программы и результатов, полученных ручным способом:
| Ручной способ вычисления | Программный способ вычисления | ||
| Х | Y | X | Y |
| 0 | 0,82 | 0 | 0,82 |
| 0,2 | 0,75 | 0,2 | 0,7516 |
| 0,4 | 0,77 | 0,4 | 0,770248 |
| 0,6 | 0,85 | 0,6 | 0,856793 |
| 0,8 | 0,99 | 0,8 | 0,996299 |
Из приведенного сравнения можно сделать вывод, что один результат отличается от другого тем, что в примере, решенном программным способом ответ вычисляется с наибольшей точностью, чем при ручном способе. Это может быть связано с тем, что в ручном способе результат округляется для удобства вычисления примера.
Решение дифференциальных уравнений методом Эйлера можно также отобразить в графическом виде:
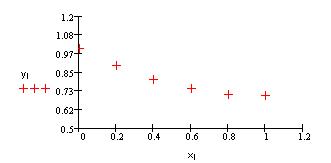
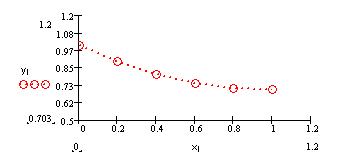
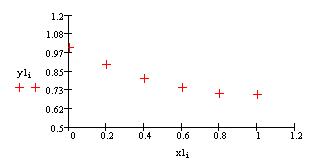
Рис.3.Графическое изображение решения примера y’=2x+y
Как видно из рис.3 графиком решения уравнения является кривая , форма которой зависит от количества разбиений интервала.
По результатам выполненной работы можно сделать вывод, что решение дифференциальных уравнений методом Эйлера является методом вычисления со средней точностью и точность вычисления данного метода зависит от количества разбиений интервала интегрирования. При сравнении результатов решенными разными способами можно сказать, что данный метод был верно реализован на языке программирования Microsoft Visual C++. Полученные результаты сходятся с небольшой погрешностью.
Список литературы.
1. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения), Н.С. Бахвалов. Главная редакция физико- математической литературы изд-ва «Наука», М., 1975г.
2. Методы, теории обыкновенных дифференциальных уравнений. Н.И. Гаврилов . Государственное издательство «Высшая школа» Москва-1962г.
3. В.В.Пак., Ю.Л. Носенко. Высшая математика: Учебник.- Д.: Сталкер, 1997г.
4. Б. П. Демидович, И. А. Марон Основы вычислительной математике. – М., 1966
5. Загускин В. Л. – Справочник по численным методам решения уравнений. – М.: ФИЗМАТГИЗ, 1960. – 216 с.
6. Либерти, Джесс.
Освой самостоятельно С++ за 21 день, 4-е издание.:Пер с англ.-М.: Издательский дом «Вильямс», 2003.-832с.
7. П.Нортон, П.Иао «Программирование на С++ в среде Windows» («Диалектика» Киев 2003г.)
8. Янг М. Microsoft Visual C++ - М.:ЭНТРОП, 2000.
9. Марченко А.И., Марченко Л.А. – Программирование в среде
Turbo Pascal 7.0 – К.: ВЕК+, М.: Бином Универсал, 1998. – 496 с.
10. Высшая математика: Справ. материалы: Книга для учащихся .- М.:
Просвещение, 1988.-416 с.: ил.
Приложение.
Листинг программы.
#include<iostream>
using namespace std;
void func(double& Xi, double& Yi,double kx, double ky, double h);
int main()
{
double h,Xi,Yi,Xkon,kx,ky;
int n;
cout<<"\t"<<"\t"<<"************************************************n";
cout<<"\t"<<"\t"<<"* * "<<"\n";
cout<<"\t"<<"\t"<<"* Reshenie difurov 1 poryadka methodom Eulera *"<<"\n";
cout<<"\t"<<"\t"<<"*************************************************
cout<<endl;
cout<<"Vvedite nachaloe znachenie intervala [a,b]=";
cin>>Xi;
cout<<"Vvedite konechoe znachenie intervala [a,b]=";
cin>>Xkon;
cout<<"Vvedite chislo shagov=";
cin>>n;
h=(Xkon- Xi)/n;
cout<<endl;
cout<<"Vvedite nachalnoe uslovie y=";
cin>>Yi;
cout<<"Vvedite koefitsient pri x=";
cin>>kx;
cout<<"Vvedite koefitsient pri y=";
cin>>ky;
cout<<"|Interval|Chislo shagov|Shag prirasheniya|Nacalnoe Y|Uravnenie vida:| "<<"\n";
cout<<"|--------|-------------|-----------------|----------|---------------|"<<"\n";
cout<<"|"<<"["<<Xi<<","<<Xkon<<"]" <<" |"<<n<<" |"<<h<<" |"<<Yi<<" |"<<"y'="<<kx<<"x"<<"+"<<ky<<"y"<<" |"<<"\n";
cout<<endl;
cout<<endl;
for (int i=1;i<=n;i++)
{
func(Xi,Yi,kx,ky,h);
cout<<"\n";
}
return 0;
}
void func(double& Xi, double& Yi, double kx, double ky, double h)
{
double f1,Yprom,a,Xprom;
f1=(kx*Xi)+(ky*Yi);
Yprom=Yi+f1*(h/2);
Xprom=Xi+h/2;
a=kx*Xprom-Yprom;
Yi=Yi+a*h;
cout<<"\t"<<"\t"<<"Interval x="<<Xi<<"\t"<<" Resultat y="<<Yi;
Xi=Xi+h;
}
Похожие работы
... ; D(x,y) – функция,возвращающая значение в виде вектора n элементов, содержащих первые производные неизвестных функций. 2.1 Метод Эйлера Если задачу об отыскании всех решений дифференциального уравнения удается свести к конечному числу алгебраических операций, операций интегрирования и дифференцирования известных функций, то говорят, что уравнение интегрируется в квадратурах. В приложениях ...
... шаг интегрирования ; tp – время интегрирования трех точечным методом прогноза и коррекции , ta – время интегрирования по методу Адамса-Башфорта , NU – массив начальных условий . Данная процедура способна производить решения систем линейных дифференциальных уравнений произвольного размера , на произвольном промежутке времени интегрирования . Вычисленные данные записываются в файлы prandcom*.df . ...
... значениями и корнями дифференциального уравнения Y(I), квадрат разности, а также производит их суммирование. Далее находится величина погрешности аппроксимации и все данные выводятся на экран. Общая программа решения дифференциального уравнения с последующей аппроксимацией результатов представлена на рис. 7 вместе с программой решения дифференциального уравнения, так как из нее получают значения ...
... , является важнейшей вспомогательной научно-технической задачей . Целью данной курсовой работы является разработка алгоритма решения систем линейных дифференциальных уравнений первого порядка пяти точечным методом прогноза и коррекции Адамса-Башфорта . 1. ПОСТАНОВКА ЗАДАЧИ Рассмотрим произвольную систему линейных дифференциальных уравнений первого порядка : ...
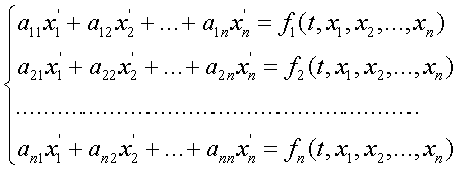
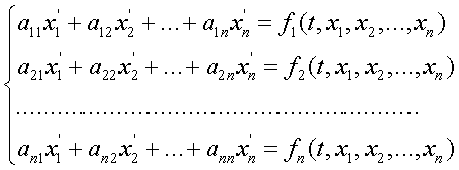

0 комментариев