Навигация
5.1. Расчёт величины S и h
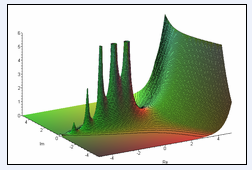
y=sh(x) - исходная функция
Найдем первую и вторую производную y
y'=ch(x) у''=sh(x)
|f'max| = 1.128 |f''max| = 0.521
Зная |f''max| найдем s и h
S ³ (n + 1 - log2((m+1)!)/|f(m+1)max|)/(m+1) , где n = 8 и m =1
Вычисляя получим s = 4
Тогда h = 2-s = 2-4 = 0.0625
5.2.Выбор масштабных коэффициентов
Мf(x) =
Mf(xs) = ![]() = 26 Mf '(x) =
= 26 Mf '(x) = ![]() = 25 Mx=
= 25 Mx=![]() =27
=27
6.Масштабирование алгоритма
f(x) = f(xs) + D xn-s×f'(xs),
F(X)/Mf(x) = F(Xs)/Mf(xs) + (D Xn-s/ MDx)×F'(Xs)/ Mf '(x)
Умножим все выражение на Mf(x)
F(X) = F(Xs)×Mf(x)/Mf(xs) + D Xn-s×F'(Xs) Mf(x)/(Mf '(x)×MDx)
Подставляя значения полученные выше получим
F(X) = F(Xs) + 2-5 ×D Xn-s×F'(Xs)
где F(X)=f(x)×Mf(x), F(Xs)=f(xs)×Mf(xs), D Xn-s= D xn-s×MDx,
F'(Xs)= f'(xs)×Mf '(x), X = x*Mx - масштабированные значения
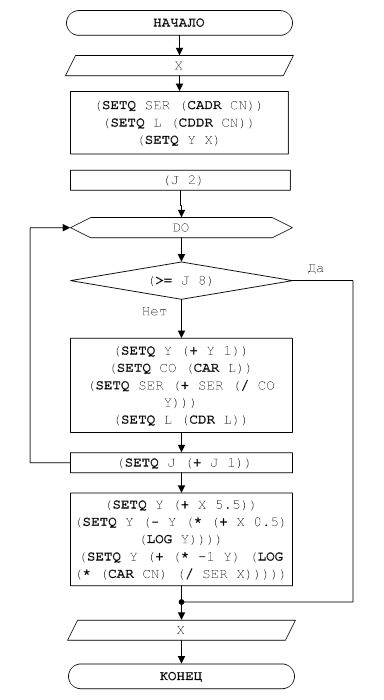
7. Граф – схема программы

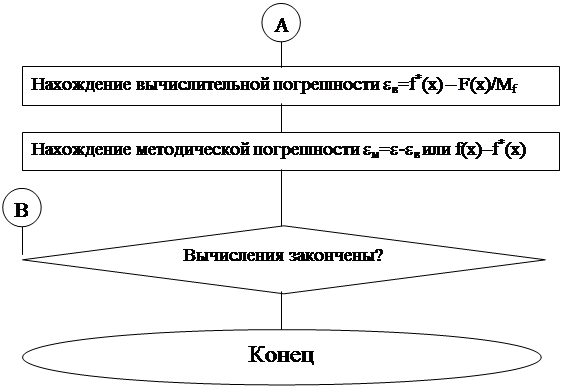
8. Листинг и описание подпрограммы функции
8.1.Листинг подпрограммы функции
function Fx(masFx,masFhx:m;Xm:word;var ad:word):longint;
var
dx,fx1:word;
begin
ad:=Xm shr 3;
dx:=Xm and $6;
fx1:=dx*masFhx[ad];
fx1:=fx1 shr 5;
Fx:=masFx[ad]+fx1;
end;
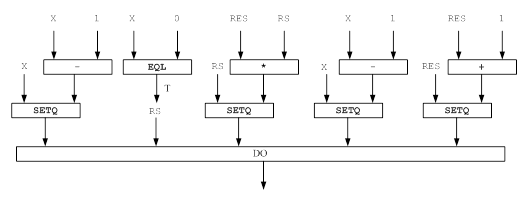
8.2. граф – схема алгоритма

9. Листинг программы
program kir;
uses crt,dos,graph;
type
m=array[0..8] of word;
const
h=0.0625;
Mh=64;
Mf=64;
Mfh=32;
Mx=128;
function Fx(masFx,masFhx:m;Xm:word;var ad:word):longint;
var
dx,fx1:word;
begin
ad:=Xm shr 3;
dx:=Xm and $6;
fx1:=dx*masFhx[ad];
fx1:=fx1 shr 5;
Fx:=masFx[ad]+fx1;
end;
var
masFx,masFhx:m;
masfxs,masfhxs,x:array[0..8] of real;
i,Xm,ad:word;
work,F,fxn,e,ev,em,fz:real;
gd,gm:integer;
xnext,xprev,y1next,y1prev:integer;
y2next,y2prev,y3next,y3prev:integer;
y4next,y4prev:integer;
begin
clrscr;
for i:=0 to 8 do begin
x[i]:=h*i;
masfxs[i]:= (exp(x[i])-exp(-x[i]))/2;
masfhxs[i]:= (exp(x[i])+exp(-x[i]))/2;
masFx[i]:=trunc(masfxs[i]*Mf);
masFhx[i]:=trunc(masfhxs[i]*Mfh);
end;
work:=0;
repeat
begin
Xm:=trunc(work*Mx);
F:=Fx(masFx,masFhx,Xm,ad);
fxn:=(exp(work)-exp(-work))/2;
e:=fxn-F/Mf;
fz:=masfxs[ad]+(work-x[ad])*masfhxs[ad];
ev:=fz-F/Mf;
em:=e-ev;
write(' ',work:5:4,' ',Xm:2,' ',fxn:4:4,' ',F:4:0,' ');
writeln(e:4:4,' ',ev:4:4,' ',em:4:4);
work:=work+h/4;
end;
until work>0.5;
writeln(' x X f(x) F(x) E Ev Em');
readln;
gd:=detect;
initgraph(gd,gm,'c:\language\bp\bgi');
cleardevice;
floodfill (0,0,white);
setcolor(black);
line(0,0,0,480);
line(0,240,640,240);
work:=0;
xnext:=1;
xprev:=0;
y2next:=240;
y1prev:=240-trunc((exp(work)-exp(-work))*120);y2prev:=240;
y3prev:=240;y4prev:=240;
repeat
begin
work:=work+h/4;
fxn:= (exp(work)-exp(-work))/2;
y1next:=240-trunc(fxn*240);
setcolor(green);
line(xprev,y1prev,xnext,y1next);
y1prev:=y1next;
Xm:=trunc(work*Mx);
F:=Fx(masFx,masFhx,Xm,ad);
e:=fxn-F/Mf;
y2next:=240-trunc(e*240);
setcolor(cyan);
line(xprev,y2prev,xnext,y2next);
y2prev:=y2next;
fz:=masfxs[ad]+(work-x[ad])*masfhxs[ad];
ev:=fz-F/Mf;
y3next:=240-trunc(ev*240);
setcolor(magenta);
line(xprev,y3prev,xnext,y3next);
y3prev:=y3next;
em:=e-ev;
y4next:=240-trunc(em*240);
setcolor(lightgray);
line(xprev,y4prev,xnext,y4next);
y4prev:=y4next;
xprev:=xnext;
xnext:=xnext+trunc(64*work);
end;
until work=0.5;
setcolor(green);
outtextxy(0,470,'f(x)');
setcolor(cyan);
outtextxy(40,470,'E');
setcolor(magenta);
outtextxy(60,470,'Ev');
setcolor(lightgray);
outtextxy(90,470,'Em');
readln;
end.
9. Результаты работы программы
0.1563 20 0.1569 12 -0.0306 -0.0307 0.0001
0.1719 22 0.1727 14 -0.0460 -0.0462 0.0002
0.1875 24 0.1886 12 0.0011 0.0011 0.0000
0.2031 26 0.2045 14 -0.0142 -0.0142 0.0000
0.2188 28 0.2205 16 -0.0295 -0.0296 0.0001
0.2344 30 0.2365 18 -0.0447 -0.0449 0.0002
0.2500 32 0.2526 16 0.0026 0.0026 0.0000
0.2656 34 0.2688 18 -0.0125 -0.0125 0.0000
0.2813 36 0.2850 20 -0.0275 -0.0277 0.0001
0.2969 38 0.3013 22 -0.0425 -0.0428 0.0003
0.3125 40 0.3176 20 0.0051 0.0051 0.0000
0.3281 42 0.3340 22 -0.0097 -0.0097 0.0000
0.3438 44 0.3506 24 -0.0244 -0.0246 0.0002
0.3594 46 0.3672 26 -0.0391 -0.0395 0.0004
0.3750 48 0.3839 24 0.0089 0.0089 0.0000
0.3906 50 0.4006 26 -0.0056 -0.0057 0.0000
0.4063 52 0.4175 28 -0.0200 -0.0202 0.0002
0.4219 54 0.4345 30 -0.0342 -0.0347 0.0004
0.4375 56 0.4516 28 0.0141 0.0141 0.0000
0.4531 58 0.4688 30 0.0000 -0.0000 0.0001
0.4688 60 0.4861 32 -0.0139 -0.0141 0.0002
0.4844 62 0.5035 34 -0.0277 -0.0282 0.0005
0.5000 64 0.5211 33 0.0055 0.0055 0.0000
x X f(x) F(x) E Ev Em
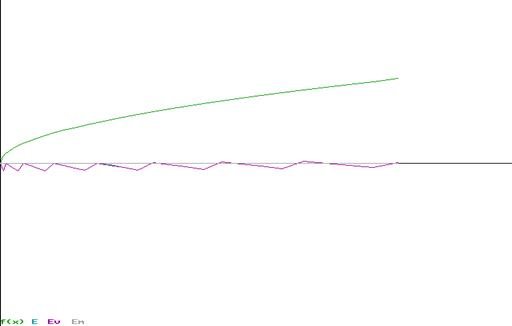
11. Заключение
В процессе выполнения курсовой работы, используя литературу и методические указания, мы выполнили проектирование алгоритма вычисления элементарной функции с использованием таблично – алгоритмического метода. Алгоритм ориентируется на целочисленные вычисления в формате байт со знаком в дополнительном коде. Разработали программу для вычисления функции на заданном интервале аппроксимации и экспериментального анализа, полной, методической и вычислительной погрешности. Программа выводит на экран графики функции и всех погрешностей на интервале аппроксимации.
12. Список литературы
1. Руководство к лабораторной работе №4 “проектирование алгоритмов вычисления элементарных функций” по курсу:
Основы обработки данных и моделирования
2. Конспект лекцийПохожие работы
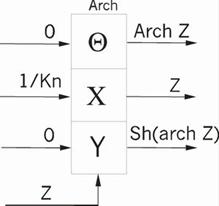
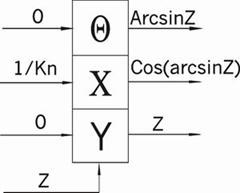
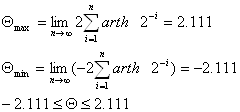
ть специализированный математический процессор для вычисления элементарных функций arcSin(Z) и arCth(Z). Эти функции можно реализовать методом Волдера «Цифра за цифрой», метод Меджита и др. Оба эти метода основаны на ряде итерационных формул, которые приведены в таблице 1.1. Основное их различие заключается в том, что в методе Меджита на первом этапе сразу рассчитываются все направляющие ...
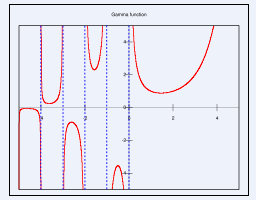
... к гамма-функции с положительным целым параметром, гамма-функции с положительным параметром, гамма-функции для множества точек. Созданная функциональная модель реализации основных способов вычисления гамма функции и ее программная реализация могут служить органической частью решения более сложных задач. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ и литературы 1. Бронштейн, И.Н. Справочник по ...
... что знак конъюнкции, как правило, опускается). Предыдущая формула приводит к важной теореме. Теорема. Всякая логическая функция может быть представлена булевой формулой, то есть как суперпозиция конъюнкции, дизъюнкции и отрицания. Действительно, для всякой функции, кроме константы 0, таким представлением может служить её СДНФ. Константу 0 можно представить булевой формулой Ø xx. А почему ...
... , которые содержат неизвестную функцию, её производные и аргументы. Обыкновенным называется дифференциальное уравнение, в котором неизвестная функция является функцией одной переменной. Если неизвестная функция является функцией многих переменных, то соответствующее уравнение называется дифференциальным уравнением в частных производных. Порядком дифференциального уравнения называется наивысший ...
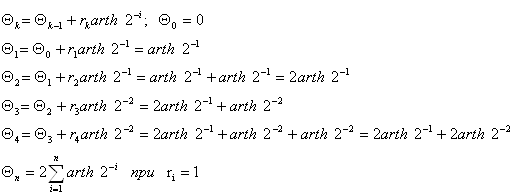
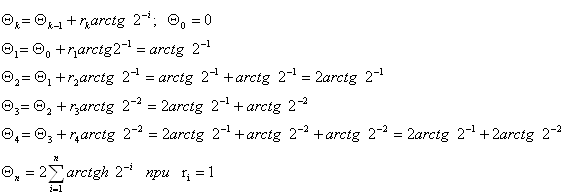
0 комментариев