Навигация
Функция многих переменных
Функция многих переменных. Предел и непрерывность функции многих переменных. Частные производные.
План.
1. Определение функции многих переменных.
2. Предел функции многих переменных. Непрерывность функции многих переменных.
3. Частные производные.
1. Обозначим через D некоторое множество точек в п-мерном пространстве.
Если задан закон f , в силу которого каждой точке М(х![]() ;...;х
;...;х![]() )
)![]() D ставится в соответствие число и, то говорят, что на множестве D определена функция и= f(х
D ставится в соответствие число и, то говорят, что на множестве D определена функция и= f(х![]() ;...;х
;...;х![]() ).
).
Множество точек М(х![]() ;...;х
;...;х![]() ), для которых функция и= f(х
), для которых функция и= f(х![]() ;...;х
;...;х![]() ) определена, называют
областью определения этой функции и обозначают D(f).
) определена, называют
областью определения этой функции и обозначают D(f).
Функции многих переменных можно обозначать одним символом и=f(М), указывая размерность пространства, которому принадлежит точка М.
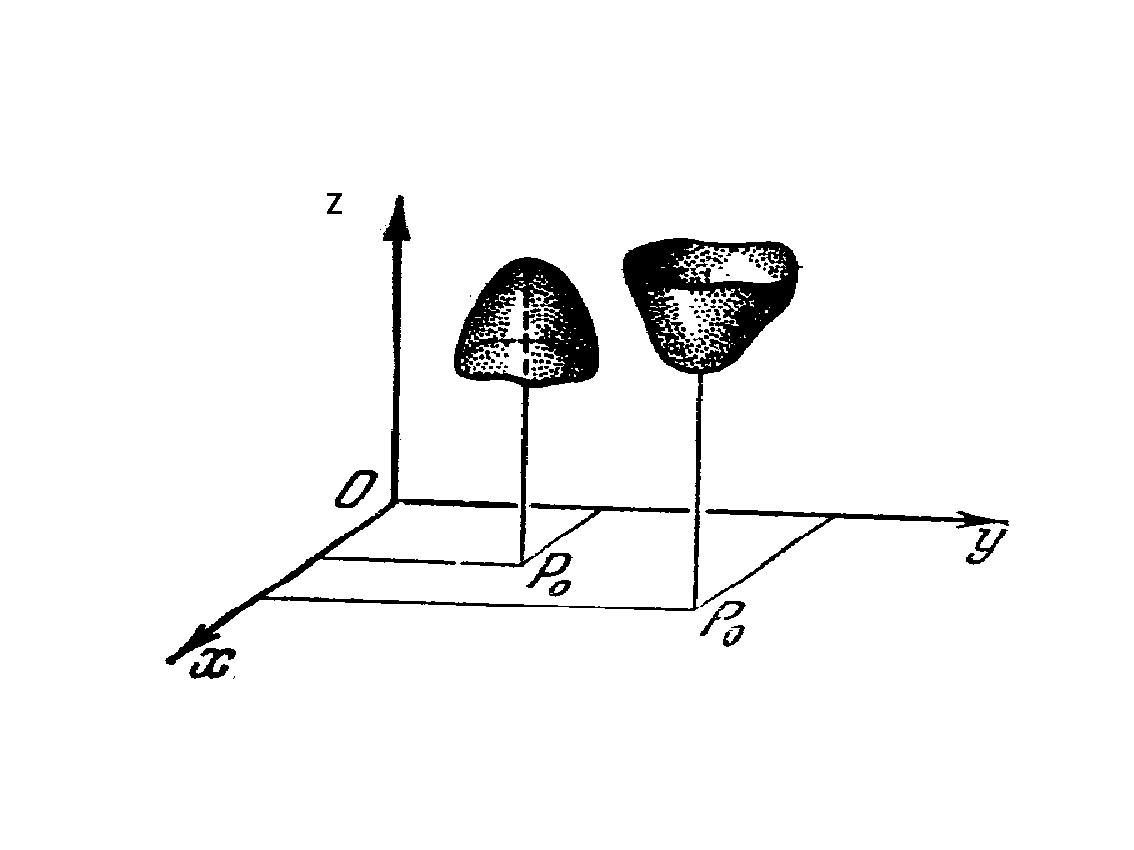
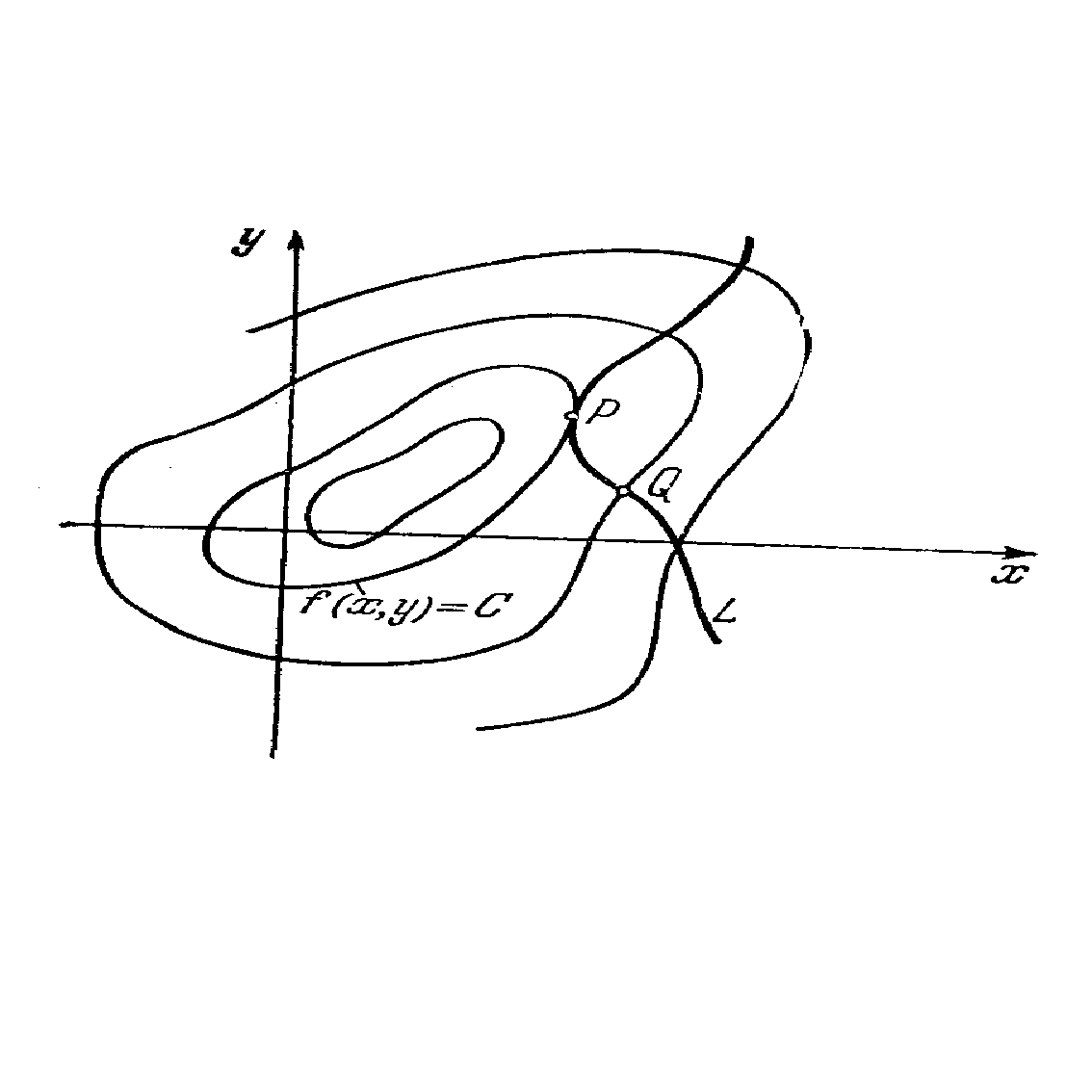
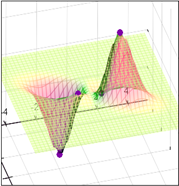
Функции двух переменных можно изобразить графически в виде некоторой поверхности.
Графиком функции двух переменных z=f(х;у) в прямоугольной системе координат Оху называется геометрическое место точек в трехмерном пространстве, координаты которых (х;у;z) удовлетворяют уравнению z=f(х;у).
2. Обозначим через ![]() (М;М
(М;М![]() ) расстояние между точками М и М
) расстояние между точками М и М![]() . Если п=2, М(х;у), М
. Если п=2, М(х;у), М![]() (х
(х![]() ;у
;у![]() ), то
), то
![]() (М;М
(М;М![]() )=
)=![]() .
.
В п-мерном пространстве
![]() (М;М
(М;М![]() )=
)=![]() .
.
Пусть на множестве D задано функцию и=f(М).
Число А называется пределом функции и=f(М) в точке М![]() , если для произвольного числа
, если для произвольного числа ![]() >0 найдётся такое число
>0 найдётся такое число ![]() >0, что для всех точек М
>0, что для всех точек М![]() D, которые удовлетворяют условию 0<
D, которые удовлетворяют условию 0<![]() (М;М
(М;М![]() )<
)<![]() , выполняется неравенство
, выполняется неравенство
![]()
![]()
![]() .
.
Свойства пределов функций одной переменной сохраняются и для функций многих переменных, то есть если функции f(М) и g(М) имеют в точке М![]() конечные пределы, то
конечные пределы, то
1. ![]() = с
= с![]() ,
,
2. ![]() =
=![]()
![]()
![]() ,
,
3. ![]() =
=![]()
![]() .
.
4. 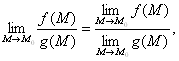 если
если ![]()
![]() .
.
Заметим, что если предел ![]() существует, то он не должен зависеть от пути, по которому точка М стремится к точке М
существует, то он не должен зависеть от пути, по которому точка М стремится к точке М![]() .
.
Функция и=f(М) называется непрерывной в точке М![]() , если
, если
![]() = f(М
= f(М![]() ).
).
Функция и=f(М) называется непрерывной на множестве D, если она непрерывна в каждой точке М![]() D.
D.
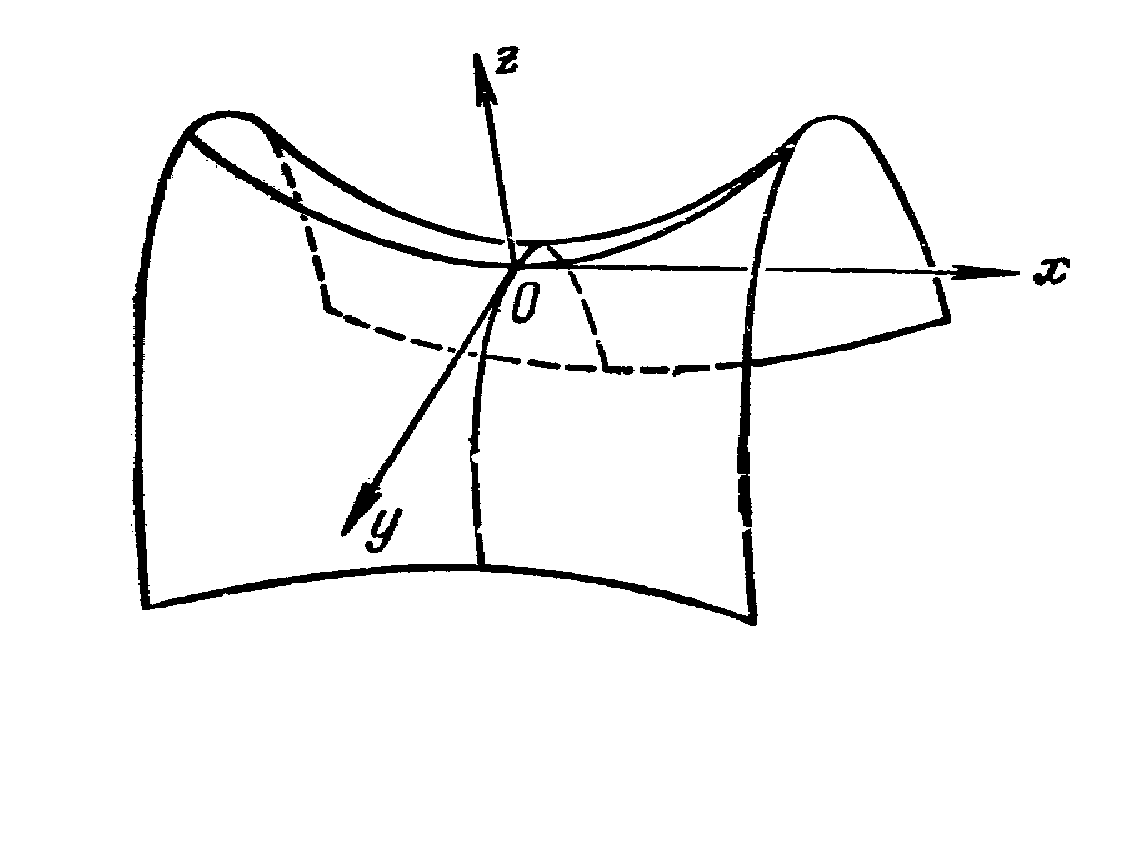
Точки, в которых непрерывность функции нарушается, называются точками разрыва функция. Точки разрыва могут быть изолированными, создавать линии разрыва, поверхности разрыва и т. д. Например, функция z=![]() имеет разрыв в точке (0;0), а функция z=
имеет разрыв в точке (0;0), а функция z=![]() имеет разрыв на параболе
имеет разрыв на параболе ![]()
3. Множество точек М, которые удовлетворяют неравенству ![]() (М;М
(М;М![]() )<
)<![]() , называют
, называют ![]() -окрестностью точки М
-окрестностью точки М![]() .
.
Пусть функция двух переменных z=f(x;у) (для большего количества переменных всё аналогично) определена в некоторой окрестности точки М(x;у). Дадим переменной х приращение ![]() так, чтобы точка (х+
так, чтобы точка (х+![]() ;у) принадлежала этой окрестности. При этом функция z=f(x;у) изменится на величину
;у) принадлежала этой окрестности. При этом функция z=f(x;у) изменится на величину
![]() ,
,
которая называется частичным приращением функции z=f(x;у) по переменной х.
Аналогично величину
![]()
называют частичным приращением функции по переменной у.
Если существует предел
![]()
![]() ,
,
то его называют частной производной функции z=f(x;у) в точке М(x;у) по переменной х и обозначают такими символами:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Аналогично
![]() =
= ![]()
![]() .
.
Из таких определений следует, что правила вычисления производных, совпадают с правилами дифференцирования функций одной переменной. Следует только помнить, что при вычислении частной производной по одной переменной остальные переменные считаются постоянными.
Частные производные характеризуют скорость изменения функции в направлении соответствующих координатных осей.
Частные производные от частных производных ![]() ,
, ![]() функции z=f(x;у) называются частными производными второго порядка. Функция двух переменных может иметь четыре частные производные второго порядка, которые обозначают так:
функции z=f(x;у) называются частными производными второго порядка. Функция двух переменных может иметь четыре частные производные второго порядка, которые обозначают так:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Производные ![]() и
и ![]() называются смешанными. Можно доказать, что если они непрерывны, то равны между собой.
называются смешанными. Можно доказать, что если они непрерывны, то равны между собой.
Частные производные от частных производных второго порядка называются частными производными третьего порядка и т. д.
Лекция 11. Тема – Дифференцируемость функции. Производная в направлении. Градиент. Локальные экстремумы.
План.
1. Дифференцируемость функции. Полный дифференциал. Дифференциалы высших порядков.
2. Производная в направлении. Градиент и его свойства.
3. Локальные экстремумы функции высших порядков.
1. Пусть функция z=f(x;у) непрерывна в некоторой окрестности точки М(x;у) вместе со своими частными производными ![]() (х;у),
(х;у),![]() (х;у). Выберем приращение
(х;у). Выберем приращение ![]() и
и ![]() так, чтобы точка (х+
так, чтобы точка (х+![]() ;у+
;у+![]() ) принадлежала рассматриваемой окрестности.
) принадлежала рассматриваемой окрестности.
Если полное приращение функции z=f(x;у) в точке М(x;у)
![]() = f(x+
= f(x+![]() ;у+
;у+![]() )- f(x;у)
)- f(x;у)
можно записать в виде
![]() =
=![]() (х;у)
(х;у)![]() +
+ ![]() (х;у)
(х;у)![]() +
+![]() ,
,
где ![]() - бесконечно малые функции при
- бесконечно малые функции при ![]()
![]() ,
, ![]()
![]() , то функция z=f(x;у) называется дифференцированной в точке М(x;у), а линейная относительно
, то функция z=f(x;у) называется дифференцированной в точке М(x;у), а линейная относительно ![]() и
и ![]() часть её полного приращения
часть её полного приращения ![]() называется полным дифференциалом функции и обозначается
называется полным дифференциалом функции и обозначается
dz=![]()
![]() +
+![]()
![]() .
.
Дифференциалами независимых переменных называют приращения этих переменных dх=![]() , dу=
, dу=![]() . Поэтому
. Поэтому
dz=![]() dх +
dх +![]() dу,
dу,
или в других обозначениях
dz=![]() dх +
dх +![]() dу.
dу.
Для функции трёх переменных и= f(x;у; z)
dи=![]() dх +
dх +![]() dу+
dу+![]() dz.
dz.
Полный дифференциал функции z=f(x;у)
dz=![]() dх +
dх +![]() dу,
dу,
который ещё называют дифференциалом первого порядка, зависит от независимых переменных х, у и от их дифференциалов dх, dу. Заметим, что дифференциалы dх, dу не зависят от х, у.
Дифференциалы второго порядка определяют по формуле
d2 z= d(dz).
Тогда
d2 z= d(![]() dх+
dх+![]() dу)=
dу)= ![]() (
(![]() dх+
dх+![]() dу) dх+
dу) dх+![]() (
(![]() dх+
dх+![]() dу) dу=
dу) dу=![]() dх2+
dх2+![]() dу dх+
dу dх+
+![]() dх dу+
dх dу+![]() dу2,
dу2,
откуда
d2 z=![]() dх2+2
dх2+2![]() dх dу+
dх dу+![]() dу2.
dу2.
Символически это можно записать так:
d2 z=(![]() dх+
dх+![]() dу)2 z.
dу)2 z.
Аналогично можно получить формулу для полного дифференциала п-го порядка:
dп z= d(dп-1 z) =(![]() dх+
dх+![]() dу)п z.
dу)п z.
2. Производная функции z=f(x;у) в направлении вектора ![]() вычисляется по формуле
вычисляется по формуле
![]()
![]()
![]() +
+![]()
![]() ,
,
где ![]() ,
, ![]() - направляющие косинусы вектора
- направляющие косинусы вектора ![]() :
:
![]() =
= ![]() ,
,
![]() =
= ![]() .
.
Если частные производные характеризуют скорость изменения функции в направлении соответствующих координатных осей, то производная в направлении вектора ![]() определяет скорость изменения функции в направлении вектора
определяет скорость изменения функции в направлении вектора ![]() .
.
Градиентом функции z=f(x;у) называется вектор
grad z=(![]() ,
,![]() ).
).
Свойства градиента
1. Производная ![]() имеет наибольшее значение, если направление вектора
имеет наибольшее значение, если направление вектора ![]() совпадает с направлением градиента, причём это наибольшее значение производной равно
совпадает с направлением градиента, причём это наибольшее значение производной равно ![]() .
.
Похожие работы
... (x, y) выполняется неравенство: . При этом, т. е. приращение функции > 0. Определение 3: Точки локальных минимума и максимума называются точками экстремума. Условные Экстремумы При отыскании экстремумов функции многих переменных часто возникают задачи, связанные с так называемым условным экстремумом. Это понятие можно разъяснить на примере функции двух переменных. Пусть заданы функция ...
... p и q, получим некоторые наборы (в зависимости от p и q) на которых функция достигает максимума. 3. Решение задачи с использованием метода покоординатного спуска 3.1 Описание метода покоординатного спуска Изложим этот метод на примере функции трех переменных . Выберем нулевое приближение . Фиксируем значения двух координат . Тогда функция будет зависеть только от одной переменной ; ...
... , Флетчера-Ривса). Методы второго порядка, использующие, кроме того, и информацию о вторых производных функции f (x) (метод Ньютона и его модификации). Метод конфигураций (Хука - Дживса) Следует выделить два этапа метода конфигураций: 1) исследование с циклическим изменением переменных и 2) ускорение поиска по образцам. Исследующий поиск начинается в точке х0, называемой старым базисом. ...
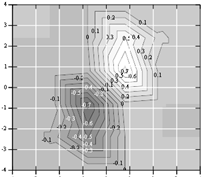
... , что и ошибки эксперимента, то итерации надо прекращать. Поскольку вблизи минимума чаще всего ~, то небольшая погрешность функции приводит к появлению довольно большой области неопределенности ~. 2. Минимум функции многих переменных 2.1 Рельеф функции Основные трудности многомерного случая удобно рассмотреть на примере функции двух переменных . Она описывает некоторую поверхность в ...


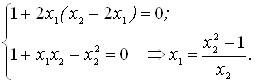
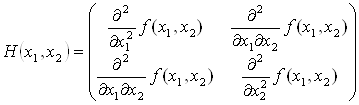


0 комментариев