Навигация
2. Построение спектрограмм.
На вход нелинейного элемента подаем 2 сигнала: АМ и гетеродин. Формулы для них выглядят соответственно:
, (2.1)
- циклическая частота несущего колебания,
- циклическая частота моделирующего колебания,
- амплитуда несущего колебания,
- амплитуда модулирующего колебания,
М – коэффициент модуляции.
, (2.2)
- амплитуда гетеродина,
- циклическая частота гетеродина,
θг – фаза гетеродина.
Выражение для выходного тока имеет вид:
(2.3)
причём U(t)=es(t)+eг(t).
Подставим в U(t) выражения (2.1) и (2.2), и получившееся выражение подставим в выражение (2.3). После раскрытия всех скобок, перемножив косинусы и понизив их степень, получим выражение(2.4), по которой строится спектрограмма:(2.4)
Для построения диаграмм улучшим наглядность. За Аn(х) обозначим амплитуду n-ой гармоники, вместо же х у меня будет стоять частота, на которой находится эта гармоника.
Подставляя заданные значения всех шести вариантов, получаем шесть спектрограмм. Числовые значения всех спектров приведены в следующих таблицах.
Таблица 2. Несущая частота больше частоты гетеродина(U0=0).
| Частота, кГц | 0 | 10 | 20 | 160 | 170 | 180 | 190 | 200 |
| Амплитуда, мА | 1,096 | 0,981 | 0,357 | 0,916 | 0,952 | 0,607 | 0,408 | 0,765 |
Таблица 3. Несущая частота меньше частоты гетеродина(U0=0).
| Частота, кГц | 0 | 8 | 12 | 16 | 20 | 28 | 144 |
| Амплитуда, мА | 1,24 | 0,82 | 0,41 | 0,15 | 1,09 | 0,41 | 0,08 |
Продолжение табл.3.
| 152 | 160 | 168 | 172 | 176 | 180 | 188 | 200 |
| 0,41 | 0,70 | 0,41 | 0,41 | 0,08 | 1,09 | 0,41 | 0,54 |
Таблица 4. Частоты равны [синхронный режим] ( U0=0).
| Частота, кГц | 0 | 14 | 28 | 112 | 126 | 140 | 154 | 168 |
| Амплитуда, мА | 2,33 | 1,22 | 0,15 | 0,08 | 0,82 | 2,74 | 0,82 | 0,08 |
Таблица 5. Несущая частота больше частоты гетеродина(U0=-0,5).
| Частота, кГц | 0 | 10 | 20 | 80 | 90 | 100 | 160 | 170 | 180 | 190 | 200 |
| Амплитуда, мА | 1,50 | 0,98 | 0,36 | 1,19 | -1,36 | -0,51 | 0,92 | 0,95 | 0,61 | 0,41 | 0,08 |
Таблица 6. Несущая частота меньше частоты гетеродина(U0=-0,5).
| Частота, кГц | 0 | 8 | 12 | 16 | 20 | 28 | 72 | 80 | 88 |
| Амплитуда, мА | 1,67 | 0,82 | 0,41 | 0,15 | 1,09 | 0,41 | -0,51 | -1,36 | -0,51 |
Продолжение табл.6.
| 100 | 144 | 152 | 160 | 168 | 172 | 176 | 180 | 188 | 200 |
| -1,36 | 0,08 | 0,41 | 0,70 | 0,41 | 0,41 | 0,08 | 1,09 | 0,41 | 0,54 |
Таблица 7. Частоты равны [синхронный режим] (U0=-0.5).
| Частота, кГц | 0 | 14 | 28 | 56 | 70 | 84 | 112 | 126 | 140 | 154 | 168 |
| Амплитуда, мА | 2,75 | 1,63 | 0,15 | -0,51 | 2,72 | -0,51 | 0,08 | 0,82 | 2,33 | 0,82 | 0,08 |
Теперь, имея всю необходимую информацию, были построены спектрограммы выходного тока.
рис. 2. Несущая частота больше частоты гетеродина(U0=0).
рис. 3. Несущая частота меньше частоты гетеродина(U0=0).
рис. 4. Частоты равны [синхронный режим] ( U0=0).
рис. 5. Несущая частота больше частоты гетеродина (U0=-0,5).
рис. 6. Несущая частота меньше частоты гетеродина(U0=-0,5).
рис. 7. Частоты равны [синхронный режим] (U0=-0,5).
Из спектров видно, что наибольшие шумы присутствуют при асинхронном режиме, когда несущая частота меньше частоты гетеродина, при U0 не равном нулю. Наименьшие же искажения относятся к случаю, когда режим синхронный, и напряжение смещения равно нулю.
Подбор параметров фильтра. Фильтрация.
Влияние добротности.
В данной работе использовался ФНЧ для фильтрации сигнала на НЧ, и резонансный фильтр для выделения сигнала на ВЧ. Их АЧХ описываются формулами соответственно:
(3.1)
(3.2)
Резонансный фильтр выделяет АМ колебание, а ФНЧ выделяет его огибающую. Параметры фильтров подбирались самостоятельно. Так как по заданию не задавалось выделять полностью всю группу ВЧ составляющих, то и не ставилась цель это сделать. ВЧ составляющие фильтровались таким образом, чтобы захватывалось как можно меньше шумов. Но и получить “идеальное” АМ колебание так же целью не ставилось.
На рисунке 8 изображёно выделение НЧ сигнала, а на рис.9 изображена фильтрация ВЧ спектральных составляющих (несущая частота меньше частоты гетеродина(U0=0)).
Асинхронный режим при U0=0.
рис. 8.
рис. 9.
На рисунках показано, как фильтруются гармоники. То, что отфильтровывается, показано жирной линией, а то, что отсекается, показано пунктиром. После фильтрации значения амплитуд
умножаются на коэффициент передачи фильтра в данной точке. Помножив на косинус с данной частотой и фазой, полученное произведение складывается с другими аналогичными произведениями соседних гармоник. Результат - нужная нам осциллограмма.
рис.10.
рис.11.
На рис 10 показана спектрограмма, для случая фильтрации, показанного на рис.8. На рис. 11 показана спектрограмма для случая, указанного на рис. 9. Это асинхронный режим. Входное АМ колебание можно увидеть на рис. 12.
рис. 12.
Период огибающей выходного НЧ колебания как видно из рис. 10 равен 0,125 мс, следовательно, частота равна 8 кГц, и совпадает с частотой входного АМ колебания.
Так как частота огибающей выходного АМ колебания равна 8кГц, следовательно, некая гармоника модулирует наш сигнал с этой частотой. Эта гармоника находится на расстоянии 8 кГц вправо-влево от несущей частоты (рис. 9). На расстоянии 12 кГц влево от несущей находится составляющая, которая отвечает за отсечку. Докажем это: отсечка начинается через каждые 0,08 мс от максимума АМ сигнала, следовательно частота гармоники искажающей АМ сигнал есть частота, находящаяся на расстоянии 12 кГц влево от частоты несущей. Остальные гармоники вносят незначительные искажения из-за их небольших амплитуд.
Аналогично, за искажение НЧ сигнала отвечают гармоника, которая находится на частоте 12 кГц. Период же НЧ колебания равен 0,125 мс,частота равна 8 кГц, что соответствует первой гармонике. Остальные гармоники вносят незначительные искажения из-за их относительно небольших амплитуд.
Входное и выходное АМ колебания схожи, но из рис. 11 видно, что в выходном присутствуют искажения, которые вносятся при преобразовании частоты.
График гетеродина приведён на рис.13 (г=600).
рис.13.
Рассмотрим синхронный режим при U0=-0,5.
На рис. 14 и 15 приведена фильтрация НЧ и ВЧ спектральных составляющих.
рис.14.
рис. 15.
На рис. 16 и 17 изображены соответственно осциллограммы НЧ и ВЧ колебания.
рис. 16
рис. 17
рис. 18.
На рис.18 изображена осциллограмма входного АМ колебания.
При синхронном режиме работы искажения минимальны. Как видно из рисунков 17 и 18 частоты модулирующих колебаний одинаковы (14кГц по заданию). Проверим это: Период модулирующего выходного АМ колебания равен 0,072мс, следовательно, частота равна 14 кГц. Минимальные искажения видны и из спектрограмм (рис. 14 и 15). Коэффициент модуляции входного АМ колебания (0,6) в 3 раза больше, чем коэффициент модуляции выходного (0,2). При синхронном режиме полученное НЧ колебание содержит в себе гораздо больше полезной информации, чем при асинхронном. Другое дело, на сколько сложно на практике добиться равенства частоты несущей и частоты гетеродина?
Спектрограмма гетеродина (г=0).
Синхронный режим при U0=0.
рис.19 Выделение НЧ гармоник.
рис.20. Фильтрация ВЧ гармоник.
рис. 21. Выходное АМ колебание.
рис. 22 НЧ колебание
рис.23. Гетеродин (г=0)
рис.24 Входное АМ колебание.
Искажения практически отсутствуют, т.к. режим синхронный и U0=0.
Рассмотрим асинхронный режим при U0=-0,5.
рис.25. Фильтрация НЧ гармоник.
рис.26. Фильтрация ВЧ гармоник.
рис. 27. Выходной АМ сигнал.
рис. 28. Выходной НЧ сигнал.
рис. 29. Входной АМ сигнал.
рис.30. Гетеродин (г=120).
Как видно из рис.26. здесь присутствует паразитная угловая модуляция. Это также видно по выходному АМ колебанию (рис.27). Заметно, что хоть режим и асинхронный, но искажений присутствует гораздо меньше, чем в случае, когда частота гетеродина больше частоты несущего колебания.
При фильтрации ВЧ гармоник, неискажённой остаётся только несущая гармоника, остальные искажаются из-за того, что коэффициент передачи фильтра в данной точке не равен единице. Причём, чем дальше от несущей находится гармоника, тем сильнее она отсекается фильтром. Уровень подавления зависит от добротности фильтра.Чем меньше добротность, тем больше отсекается фильтром.
Похожие работы
... K(p) - операторный коэффициент передачи цепи 2 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ Студенту группы 9341 Прокопьева К.В. Учебная дисциплина “Радиотехнические цепи и сигналы” 2.1 Тема работы Анализ радиотехнических сигналов и их прохождение через линейные цепи. 2.2 Цель работы Анализ радиотехнических сигналов и линейных цепей методами математического ...
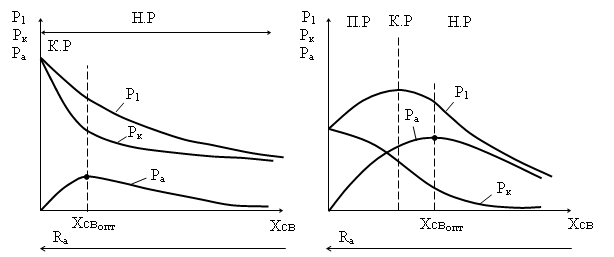
... в антенном контуре Р1=РА+РК – колебательная мощность на выходе генератора hК=РН/Р1 По данным таблиц 1 и 2 были построены нагрузочные характеристики лампового генератора с двухконтурной цепью связи с нагрузкой, полученные экспериментальным путем. Экспериментальные нагрузочные характеристики приведены на графиках 1¸6. График 1. Rахх = 4Rак Rахх = Rак ...
... фильтра является величиной конечной. так как отклик фильтра не может появиться раньше чем придет воздействие то to ³ Tc. 2) длительность Tc < ¥ Þ оптимальная фильтрация применима лишь для импульсных сигналов. При синтезе СФ в качестве входного аналогового сигнала в курсовой работе используется импульсный сигнал, построенный в соответствии с какой либо бинарной кодовой ...
... отношению к малому сигналу НЭ является линейным, но с переменным параметром (в данном случае крутизной ВАХ). Такой режим работы НЭ называется параметрическим. 1. Аппроксимация характеристик нелинейных элементов При анализе нелинейных цепей (НЦ) обычно не рассматривают процессы, происходящие внутри элементов, составляющих эту цепь, а ограничиваются лишь внешними их характеристиками. Обычно это ...


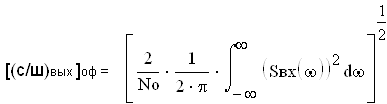

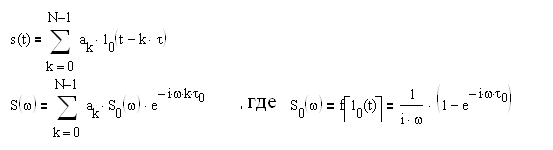
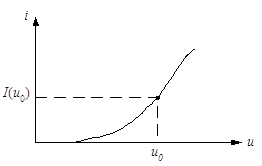
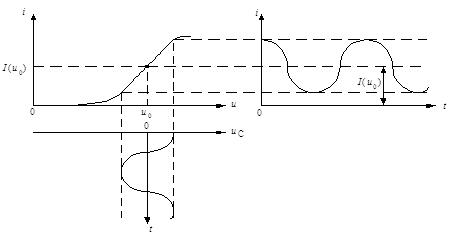

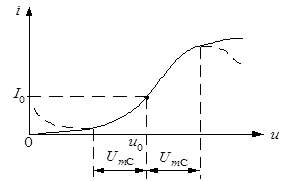
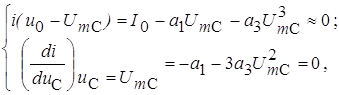
0 комментариев