Навигация
Дата выдачи: сентябрь 2000 г
7. Дата выдачи: сентябрь 2000 г.
Руководитель: ______Никифоров Н.Т.
Задание принял к выполнению: ноябрь 2000 г. _______________
Аннотация.
Курсовая работа содержит полный расчёт спектрограмм выходных токов нелинейного элемента при детектировании в синхронном и асинхронном режимах (совпадение и несовпадение частот входного сигнала и гетеродина). Входной ток, воздействующий на нелинейный элемент, является АМ - колебанием.
Расчёт коэффициентов степенного ряда производится по вольт-амперной характеристике нелинейного элемента.
Для выделения НЧ и ВЧ сигнала на рассчитанный спектр накладывается фильтр низких частот и резонансный фильтр, параметры которых выбираются самостоятельно для каждого случая.
Для расчёта спектров в работе применяется программа MathCad 8.0, а для оформления работы использовался редактор Microsoft Word 97.
Все полученные в ходе расчёта спектров распечатки сведены в приложения к работе для более лёгкого ознакомления.
Содержание.
Введение……………………………………………………………………………………………….5
Расчёт коэффициентов степенного ряда…………………………………………………………6
Расчёт и построение спектрограмм выходного тока……………………………………………7
Подбор параметров фильтров и фильтрация выходного тока………………………………….9
Выводы……………………………………………………………………………………………10
Список литературы………………………………………………………………………………11
Приложения………………………………………………………………………………………12
Приложение 1. Спектры тока на выходе детектора…………………………………………...12
Приложение 2. Асинхронный режим детектирования при U0 = 0……………………………14
Приложение 3. Синхронный режим детектирования при U0 = 0……………………………..16
Приложение 4. Асинхронный режим детектирования при U0 = 0,2 В……………………….18
Приложение 5. Асинхронный режим детектирования при U0 = 0,2 В……………………….20
Введение.
При проектировании различных радиотехнических устройств нередко возникает задача переноса спектра сигнала в область более низких частот с сохранением формы и структуры сигнала. Такую задачу можно решить, если преобразуемый сигнал подать на вход нелинейного элемента одновременно с сигналом вспомогательного генератора, называемого гетеродином. В результате, мы получим исходный сигнал с той же структурой, но сдвинутый по оси частот.
Это свойство используется при детектировании АМ - колебания, которое заключается в выделении сигнала, пропорционального закону изменения амплитуды АМ колебания, т.е. выделяется сигнал, несущий полезную информацию. Таким образом, процесс детектирования является обратным процессу модулирования сигналов, и иногда называется демодуляцией.
Итак, при детектировании на вход детектора подаётся модулированный сигнал и сигнал гетеродина, а на выходе после прохождения фильтра низких частот выделяется сигнал соответствующий исходному моделирующему колебанию. Детектор называют синхронным, а детектирование происходит с минимальными искажениями, если частоты гетеродина и модулированного сигнала будут равны, и асинхронным, и, следовательно, детектирование с более сильными искажениями, если частоты неравны.
В предлагаемой курсовой работе рассматриваются оба режима детектирования: синхронный и асинхронный, исследуются факторы, влияющие на качество детектирования, такие как: параметры НЧ фильтров, их добротность.
1. Расчёт коэффициентов степенного ряда.
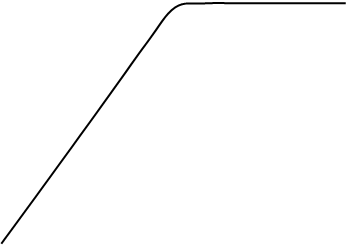
Для расчёта всех коэффициентов полинома второй степени можно воспользоваться графиком и аналитической формулой для ВАХ нелинейного элемента, которая имеет следующий вид:
Рис 1. ВАХ нелинейного элемента.
На рисунке 1 изображена ВАХ нелинейного элемента при заданном значении a2=1,3 мА/В2. Зная математическую зависимость для ВАХ, рассчитаем по формуле:
,
где U0 - это напряжение смещения рабочей точки,
коэффициенты a0 и a1, являющиеся соответственно током и крутизной ВАХ в рабочей точке. Т.к. задано два значения напряжения смещения U0, то получим шесть значений коэффициентов:
при U0 = 0 В получаем
мА
мА/В
мА/В2
при U0 = 0,2 В получаем
мА
мА/В
мА/В2
2. Расчёт и построение спектрограмм.
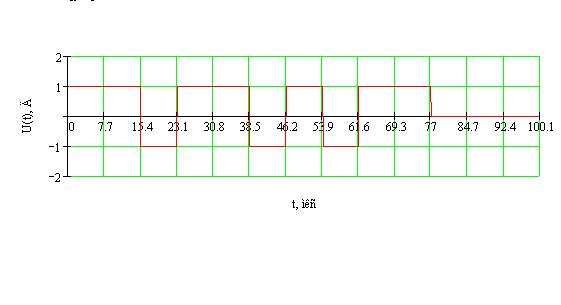
Запишем аналитические выражения для сигналов, которые подаются на вход детектора, а именно формулу для АМ - колебания:
, (2.1)
где - коэффициент модуляции,
- циклическая частота несущего колебания,
- циклическая частота моделирующего колебания,
и - амплитуды несущего и моделирующего колебаний,
Уравнение, описывающее колебания гетеродина:
, (2.2)
где - циклическая частота колебаний гетеродина,
- амплитуда колебаний гетеродина.
При степенной аппроксимации полиномом второй степени, выражение, описывающее сигнал на выходе детектора, будет иметь следующий вид:
(2.3)
где - колебание на входе детектора.
В нашем случае колебание на входе это сумма АМ - колебания и колебания гетеродина. Таким образом, подставив в выражение (2.3) вместо сумму выражений (2.1) и (2.2), раскрыв скобки, приведя подобные слагаемые и понизив степени, получим выражение полностью описывающее спектральный состав выходного тока. Выполнив все действия, получили, что:
(2.4)
Из выражения (2.4) можно легко получить спектральный состав выходного тока. Значение амплитуд гармоник соответствуют значения, стоящие перед косинусами, а значения частоты, на которой находятся гармоника, соответствует частоте в аргументе косинуса. Запишем формулы для вычисления амплитуд спектральных составляющих и соответствующих им частот:
- постоянная составляющая на нулевой частоте,
- на частоте , - на частоте , - на частоте ,
- на частоте 2, - на частоте 2, - на частоте 2,
- на частоте +, - на частоте -,
- на частоте +, - на частоте -,
- на частоте 2+, - на частоте 2-, (2.5)
- на частоте 2+2, - на частоте 2-2,
- на частоте , - на частоте ,
- на частоте , - на частоте ,
Таким образом, мы получили, что спектр выходного сигнала состоит из девятнадцати спектральных составляющих, значение которых вычисляются по формулам (2.5). Ниже приведены таблицы, содержащие значения спектральных составляющих и значения соответствующих им частот для всех шести вариантов задания.
Таблица 2. U0 = 0, f0 = 180кГц, F = 18кГц, fг = 160кГц
| f, кГц | 0 | 18 | 36 | 324 | 342 | 360 | 378 | 396 |
| Аn, мА | 0,4808 | 0,5023 | 0,08125 | 0,04063 | 0,2511 | 0,4814 | 0,2511 | 0,04063 |
Таблица 3. U0 = 0, f0 = 150кГц, F = 15кГц, fг = 180кГц
| f, кГц | 0 | 15 | 30 | 45 | 270 | 285 | 300 | 315 | 330 | 345 | 360 |
| Аn,мА | 0,29 | 0,344 | 0,258 | 0,13 | 0,04 | 0,13 | 0,185 | 0,225 | 0,208 | 0,13 | 0,104 |
Таблица 4. U0 = 0, f0 = 160кГц, F = 20кГц, fг = 160кГц
| f, кГц | 0 | 20 | 40 | 280 | 300 | 320 | 340 | 360 |
| Аn, мА | 0,4973 | 0,52 | 0,08125 | 0,04063 | 0,26 | 0,4973 | 0,26 | 0,04063 |
Таблица 5. U0 = 0.2, f0 = 180кГц, F = 18кГц, fг = 160кГц
| f, кГц | 0 | 2 | 18 | 20 | 36 | 38 | 160 | 162 | 180 | 198 |
| Аn,мА | 0,3413 | 0,13 | 0,26 | 0,208 | 0,0812 | 0,13 | 0,208 | 0,13 | 0,208 | 0,13 |
| f, кГц | 320 | 322 | 324 | 340 | 342 | 358 | 360 | 378 | 396 | |
| Аn,мА | 0,104 | 0,13 | 0,0406 | 0,208 | 0,13 | 0,13 | 0,1853 | 0,13 | 0,0406 |
Таблица 6. U0 = 0.2, f0 = 150кГц, F = 15кГц, fг = 180кГц
| f, кГц | 0 | 15 | 30 | 45 | 135 | 150 | 165 | 180 |
| Аn,мА | 0,3413 | 0,3439 | 0,2584 | 0,13 | 0,13 | 0,208 | 0,13 | 0,208 |
| f, кГц | 270 | 285 | 300 | 315 | 330 | 345 | 360 | |
| Аn,мА | 0,0406 | 0,13 | 0,1853 | 0,2252 | 0,231 | 0,13 | 0,104 |
Таблица 7. U0 = 0.2, f0 = 160кГц, F = 20кГц, fг = 160кГц
| f, кГц | 0 | 20 | 40 | 140 | 160 | 180 | 280 | 300 | 320 | 340 | 360 |
| Аn,мА | 0,549 | 0,52 | 0,081 | 0,13 | 0,416 | 0,13 | 0,041 | 0,26 | 0,497 | 0,26 | 0,041 |
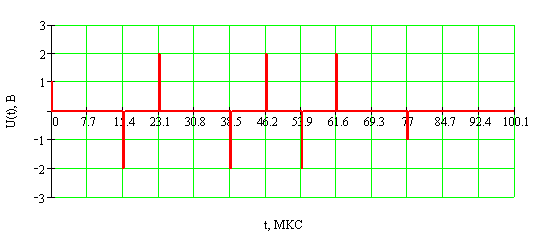
Различное количество гармоник объясняется тем, что некоторые из девятнадцати составляющих находятся на одинаковых частотах, и поэтому складываются в одну составляющую на данной частоте. С помощью вышеприведённых таблиц строятся спектры выходных токов для всех шести вариантов, которые приведены в приложении 1, причём в таблицах 4 и 7 описаны спектры при синхронном детектировании, а в остальных при асинхронном. В приложении 1 номер рисунка, на котором изображён спектр сигнала, соответствует варианту, полученному из таблицы 1 задания к данной курсовой работе. Спектрограммы изображены в том же порядке, что и таблицы 2 - 7.
Похожие работы
... K(p) - операторный коэффициент передачи цепи 2 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ Студенту группы 9341 Прокопьева К.В. Учебная дисциплина “Радиотехнические цепи и сигналы” 2.1 Тема работы Анализ радиотехнических сигналов и их прохождение через линейные цепи. 2.2 Цель работы Анализ радиотехнических сигналов и линейных цепей методами математического ...
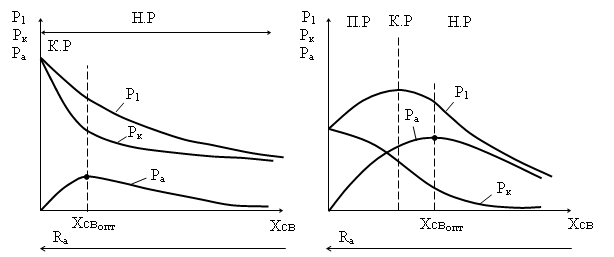
... в антенном контуре Р1=РА+РК – колебательная мощность на выходе генератора hК=РН/Р1 По данным таблиц 1 и 2 были построены нагрузочные характеристики лампового генератора с двухконтурной цепью связи с нагрузкой, полученные экспериментальным путем. Экспериментальные нагрузочные характеристики приведены на графиках 1¸6. График 1. Rахх = 4Rак Rахх = Rак ...
... фильтра является величиной конечной. так как отклик фильтра не может появиться раньше чем придет воздействие то to ³ Tc. 2) длительность Tc < ¥ Þ оптимальная фильтрация применима лишь для импульсных сигналов. При синтезе СФ в качестве входного аналогового сигнала в курсовой работе используется импульсный сигнал, построенный в соответствии с какой либо бинарной кодовой ...
... отношению к малому сигналу НЭ является линейным, но с переменным параметром (в данном случае крутизной ВАХ). Такой режим работы НЭ называется параметрическим. 1. Аппроксимация характеристик нелинейных элементов При анализе нелинейных цепей (НЦ) обычно не рассматривают процессы, происходящие внутри элементов, составляющих эту цепь, а ограничиваются лишь внешними их характеристиками. Обычно это ...


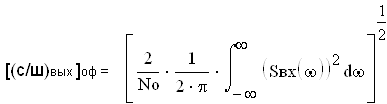

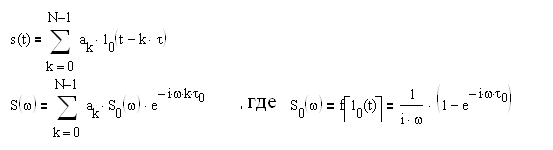
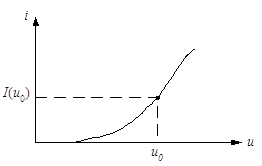
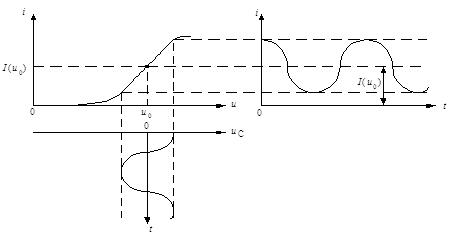

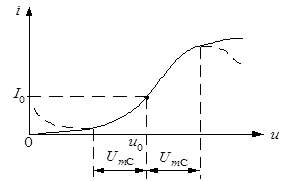
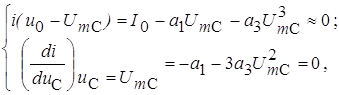
0 комментариев