Навигация
Подбор параметров фильтров и фильтрация выходного тока
3. Подбор параметров фильтров и фильтрация выходного тока.
Чтобы исследовать получившийся на выходе детектора сигнал, целесообразно выделить из целого спектра отдельную его часть на частотах и , т.к. спектр входного колебания смещается по оси частот. Если при этом частота несущего колебания равна частоте гетеродина, то спектр на низких частотах содержит практически копию спектра моделирующего колебания. Поэтому, фильтруя отдельные части спектра, можно оценить качество детектирования. Для того чтобы из спектра выделить низкочастотные составляющие, будем использовать фильтр низких частот, а для выделения более высокочастотной части - резонансный полосовой фильтр. Зададим оба фильтра так, чтобы их АЧХ приблизились по форме и структуре к АЧХ соответствующих фильтров Баттерворта. Из параметров для полосового фильтра определим резонансную частоту ωр= и добротность Q = ωр/Δω, где Δω = 2*Ω - ширина полосы пропускания. Для фильтра НЧ зададим частоту среза fср = Ω. Аналитические выражения, описывающие передаточные функции фильтров, приведены ниже:
- для фильтра низких частот, (3.1)
- для полосового фильтра (3.2)
Для рассмотрения возьмём четыре различных варианта детектирования: синхронный режим для двух значений начального смещения и асинхронный режим для тех же значений U0. Все полученные распечатки и фрагменты осциллограмм представлены в приложениях 2 - 5, соответственно для каждого из вариантов. Изменяя при фильтрации значения добротности фильтров, можно добиться оптимального выделения сигналов из спектра. Так, увеличивая добротность полосового фильтра, можно избавиться от ненужных шумовых спектральных составляющих, однако одновременно существует риск слишком сильно ослабить боковые составляющие АМ колебания, что в свою очередь приведёт к изменению формы колебания, т.е. изменится коэффициент модуляции.
После фильтрации, полученные значения пропущенных фильтром гармоник умножаются на косинус соответствующей им частоты, а затем все они складываются. В результате мы получаем осциллограмму сигнала с выхода фильтра.
Изучив полученные осциллограммы выходных сигналов, можно сделать вывод, что наиболее качественное детектирование АМ сигнала происходит в синхронном режиме при равных частотах гетеродина и несущего колебания. В этом случае спектр переносится в область нулевой частоты без внесения помех, и отфильтрованный НЧ сигнал практически совпадает с огибающей АМ колебания. В асинхронном режиме исходный спектр либо полностью не переносится, при частоте гетеродина меньшей частоты несущей, либо зеркально отображается, если частота гетеродина больше, что в любом случае вносит искажения в НЧ сигнал. Подобный случай можно наблюдать в приложении 4, где в НЧ сигнал вносятся искажения паразитные гармоники. Как видно из рисунка 4.5 в сигнал кроме полезных гармоник на частотах 0 и 20 кГц входят паразитные гармоники на частоте 18 кГц и 2 кГц, последняя и создаёт биения с частотой 2 кГц (см. рисунок). Кроме того, искажается и АМ сигнал на несущей частоте (рисунки 4.4 и 4.6). Частота огибающей не изменяется, но в модуляции принимает участие ещё и составляющая, которая находится на расстоянии 2 кГц от центральной составляющей и вносит паразитные колебание с частотой 2 кГц (см. рисунок 4.6).
4. Выводы.
В данной работе выполнен расчет коэффициентов степенного полинома для различных напряжений смещения, а также рассчитан спектр входного напряжения, который включает три составляющие (центральную и 2 боковых), т. к. входной сигнал представляет собой АМ колебание. Также рассчитан и построен спектр выходного тока для различных напряжений смещения, частот и фаз гетеродина. Амплитуды гармоник выходного тока оказались одинаковыми для равных напряжений смещения. Но амплитуда гармоники не всегда совпадает с амплитудой в спектре на той же частоте, происходит как бы «отскок» от оси координат, несколько гармоник оказались на одной частоте и их амплитуды сложились.
Следует заметить о фазе гетеродина. При г = 0 ток достигает максимума, а при г = /2 или 3/2 ток достигает минимума. Выходной ток зависит не только от частот и фазы гетеродина, но и от напряжения смещения. При U0=0 В спектр как бы «сгущается», т.е. амплитуды спектральных составляющих на НЧ и ВЧ увеличиваются (как следствие после фильтрации, НЧ и ВЧ сигналы получают меньше искажений), а при U0=0.4 В спектр «рассредоточивается» (сигналы на выходах фильтра более искажены).
Для выделения сигналов из спектра использовались два фильтра: ФНЧ и полосовой фильтр, для которых были рассчитаны добротности, частоты резонанса и среза. С их помощью были получены выходные характеристики для разных режимов работы детектора.
Список литературы
И. С. Гоноровский. «Радиотехнические цепи и сигналы».
М. «Советское радио». 1994. Изд. 5, перераб. и доп.
С. И. Баскаков. «Радиотехнические цепи и сигналы».
М. «Высшая школа». 2000. Изд. 3, перераб. и доп.
В. С. Андреев. «Теория нелинейных электрических цепей».
М. «Радио и связь». 1988.
Н. Т. Никифоров. Конспект лекций по курсу
«Радиотехнические цепи и сигналы».
Приложение 1.
Спектры тока на выходе детектора.
Рис 1.1. U0 = 0, f0 = 180кГц, F = 18кГц, fг = 160кГц
Рис 1.2. U0 = 0, f0 = 150кГц, F = 15кГц, fг = 180кГц
Рис 1.3. U0 = 0, f0 = 160кГц, F = 20кГц, fг = 160кГц
Рис 1.4. U0 = 0.2, f0 = 180кГц, F = 18кГц, fг = 160кГц
Рис 1.5. U0 = 0.2, f0 = 150кГц, F = 15кГц, fг = 180кГц
Рис 1.6. U0 = 0.2, f0 = 160кГц, F = 20кГц, fг = 160кГц
Приложение 2.
Асинхронный режим детектирования при U0 = 0.
f0 = 180кГц, F = 18кГц, fг = 160кГц
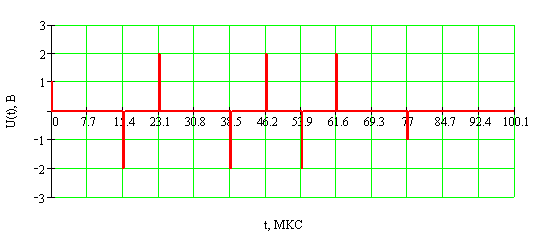
Рис 2.1. Спектр с НЧ фильтром
Рис 2.2. Спектр с полосовым фильтром.
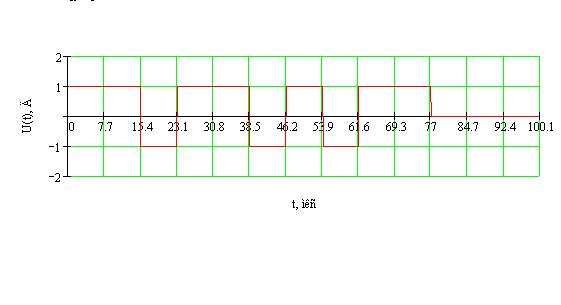
Рис 2.3. Входной сигнал.
Рис 2.4. ВЧ сигнал на выходе фильтра.
Рис 2.5. НЧ сигнал на выходе фильтра.
Рис 2.6. Колебание гетеродина при г=300.
Приложение 3.
Синхронный режим детектирования при U0 = 0.
f0 = 160кГц, F = 20кГц, fг = 160кГц
Рис 3.1. Спектр с НЧ фильтром
Рис 3.2. Спектр с полосовым фильтром.
Рис 3.3. Входной сигнал.
Рис 3.4. ВЧ сигнал на выходе фильтра.
Рис 3.5. НЧ сигнал на выходе фильтра.
Рис 3.6 Колебание гетеродина при г=00.
Приложение 4.
Асинхронный режим детектирования при U0 = 0,2 В.
f0 = 180кГц, F = 18кГц, fг = 160кГц
Рис 4.1. Спектр с НЧ фильтром.
Рис 4.2. Спектр с полосовым фильтром.
Рис 4.3. Входной сигнал.
Рис 4.4. ВЧ сигнал на выходе фильтра.
Рис 4.5. НЧ сигнал на выходе фильтра.
Рис 4.6. ВЧ сигнал на выходе на длинном интервале времени.
Приложение 5.
Асинхронный режим детектирования при U0 = 0,2 В.
f0 = 160кГц, F = 20кГц, fг = 160кГц
Рис 5.1. Спектр с НЧ фильтром.
Рис 5.2. Спектр с полосовым фильтром.
Рис 5.3. Входной сигнал.
Рис 5.4 ВЧ сигнал на выходе фильтра.
Рис 5.5. НЧ сигнал на выходе фильтр
Похожие работы
... K(p) - операторный коэффициент передачи цепи 2 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ Студенту группы 9341 Прокопьева К.В. Учебная дисциплина “Радиотехнические цепи и сигналы” 2.1 Тема работы Анализ радиотехнических сигналов и их прохождение через линейные цепи. 2.2 Цель работы Анализ радиотехнических сигналов и линейных цепей методами математического ...
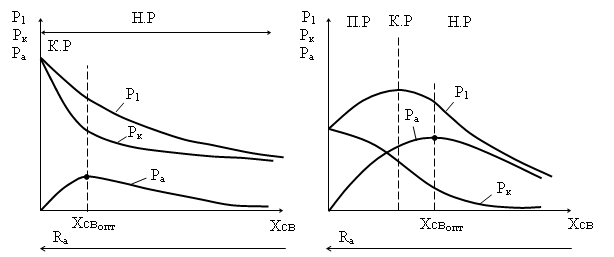
... в антенном контуре Р1=РА+РК – колебательная мощность на выходе генератора hК=РН/Р1 По данным таблиц 1 и 2 были построены нагрузочные характеристики лампового генератора с двухконтурной цепью связи с нагрузкой, полученные экспериментальным путем. Экспериментальные нагрузочные характеристики приведены на графиках 1¸6. График 1. Rахх = 4Rак Rахх = Rак ...
... фильтра является величиной конечной. так как отклик фильтра не может появиться раньше чем придет воздействие то to ³ Tc. 2) длительность Tc < ¥ Þ оптимальная фильтрация применима лишь для импульсных сигналов. При синтезе СФ в качестве входного аналогового сигнала в курсовой работе используется импульсный сигнал, построенный в соответствии с какой либо бинарной кодовой ...
... отношению к малому сигналу НЭ является линейным, но с переменным параметром (в данном случае крутизной ВАХ). Такой режим работы НЭ называется параметрическим. 1. Аппроксимация характеристик нелинейных элементов При анализе нелинейных цепей (НЦ) обычно не рассматривают процессы, происходящие внутри элементов, составляющих эту цепь, а ограничиваются лишь внешними их характеристиками. Обычно это ...


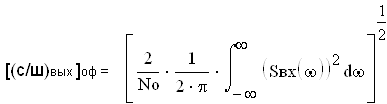

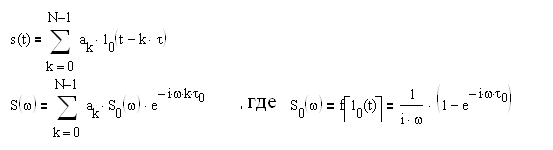

0 комментариев