Навигация
Теория распределения информации
Министерство науки и высшего образования Республики Казахстан
Алматинский институт энергетики и связи
Кафедра Автоматической электросвязи
КУРСОВАЯ РАБОТАпо дисциплине: Теория распределения информации
ШИФР:
ГРУППА:
ВЫПОЛНИЛ:
ПРОВЕРИЛ:
Г. АЛМАТЫ, 1999 Г.
ЗАДАНИЕ 1.
1. Построить огибающую распределения вероятности занятия линии в пучке из V, на каждую из которых поступает интенсивность нагрузки а при условии, что:
а) N >> V; б) N V; в) N, V
2. Для каждого используемого распределения рассчитать среднее число занятых линий и их дисперсию.
Для расчета число линий в пучке определить из следующего выражения:
V= ;
целая часть полученного числа, где NN – номер варианта.
Средняя интенсивность нагрузки, поступающей на одну линию:
а = 0,2+0,01 * NN
Примечания:
· Для огибающей распределения привести таблицу в виде:
| Р(i) | ||||
| i |
· В распределении Пуассона привести шесть – восемь составляющих, включая значение вероятности для i = (целая часть А)
· А = а * V
Решение:
Случайной называют такую величину, которая в результате эксперимента принимает какое то определенное значение, заранее не известное и зависящее от случайных причин, которые наперед предугадать невозможно. Различают дискретные и непрерывные случайные величины. Дискретная случайная величина определяется распределением вероятностей, непрерывная случайная величина – функцией распределения основными характеристиками случайной величины являются математическое ожидание и дисперсия.
Определим исходные данные для расчета:
V=
a = 0.2 + 0.01 * 11 = 0.31 Эрл (средняя интенсивность нагрузки)
А = а * V = 0,31 * 11 = 3,41 » 4 Эрл (нагрузка)
а) Определим вероятности занятия линий в пучке из V = 11, при условии N >> V (N – число источников нагрузки).
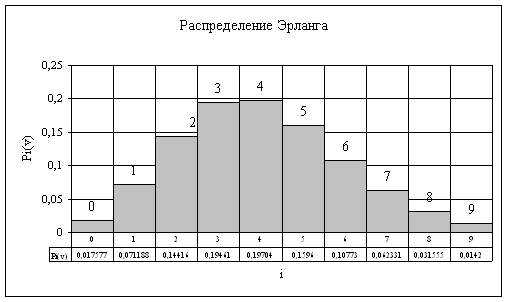
Для этого используем распределение Эрланга, представляющее собой усеченное распределение Пуассона, в котором взяты первые V+1 значения и пронумерованы так, чтобы сумма вероятностей была равна единице.
Распределение Эрланга имеет вид:
Pi(V) = , ,
где Pi(V) – вероятность занятия любых i линий в пучке из V.
Для определения составляющих распределения Эрланга можно применить следующее реккурентное соотношение:
Математическое ожидание и дисперсия числа занятых линий соответственно равны:
где Pv –вероятность занятости всех линий в пучке из V.
Произведем расчет:
Р0 =
Р1 = Р0 * = 0,072 Р2 = Р1 * = 0,144
Р3 = Р2 * = 0,192 Р4 = Р3 * = 0,192
Р5= Р4 * = 0,153 Р6 = Р5 * = 0,102
Р7 = Р6 * = 0,058 Р8 = Р7 * = 0,029
Р9 = Р8 * = 0,012 Р10 = Р9 * = 4,8 * 10-3
Р11 = Р10* = 1,7 * 10-3
M( i ) = 4 * (1 - 1,7 * 10-3) = 3,99
D( i ) = 3,99 – 4 * 1,7 * 10-3 * (11 – 3,99) = 3,94
Данные результаты вычислений сведем в таблицу 1:
Таблица 1
| P( i ) | 0,018 | 0,072 | 0,144 | 0,192 | 0,192 | 0,153 | 0,102 | 0,058 | 0,029 | 0,012 | 0,0048 | 0,0017 |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
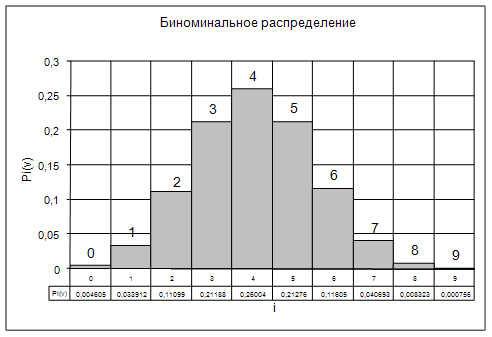
б) Определим вероятность занятия линий в пучке из V=11, при условии N@V. Применим распределение Бернулли (биноминальное распределение), которое имеет вид:
где: Pi(V) – вероятность занятия любых i линий в пучке из V;
- число сочетаний из V по i (i = 0, V)
,
а – средняя интенсивность поступающей нагрузки на одну линию
V-линейного пучка от N источников.
Для вычисления вероятностей можно воспользоваться следующей рекурентной формулой:
Математическое ожидание и дисперсия числа занятых линий соответственно равны:
M( i ) = V*a; D( i ) = V * a * (1-a)
Произведем расчет:
;
Р1 = 16,8*10-3*
Р2 = 16,8*10-3*
Р3 = 16,8*10-3*
Р4 = 16,8*10-3*
Р5 = 16,8*10-3*
Р6 = 16,8*10-3*
Р7 = 16,8*10-3*
Р8 = 16,8*10-3*
Р9 = 16,8*10-3*
Р10 = 16,8*10-3*
Р11 = 16,8*10-3*
M( i ) = 11 * 0,31 = 3,41; D( i ) = 11 * 0,31 * (1 – 0,31) = 2,35
Результаты вычислений сведем в таблицу 2:
Таблица 2
| P(i) *10-3 | 16,8 | 82,3 | 37,7 | 22,6 | 15 | 10 | 7,5 | 5,3 | 3,7 | 2,5 | 1,5 | 0,6 |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
в) Определим вероятность занятия линий в пучке из V=11 , при условии N,V®¥.
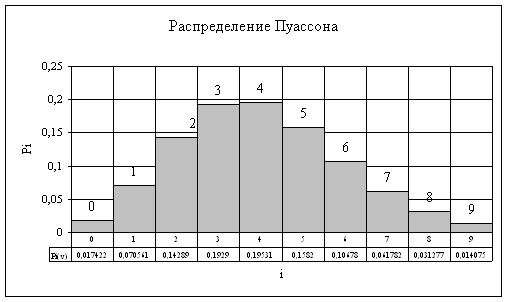
Используем распределение Пуассона, как вероятность занятия i линий в бесконечном пучке линий за промежуток времени t:
, ,
где: l - параметр потока, выз/час
lt – средняя интенсивность нагрузки поступающей на пучок линий (А=lt).
Легко показать, что:
,
Произведем расчет:
Р0 = * е-4 = 0,018 Р1 = 0,018 * = 0,036
Р4 = * 0,018 = 0,192 Р6 = 0,018 * = 0,102
Р8 = 0,018 * = 0,029 Р10 = 0,018 * = 0,0052
Р12 = 0,018 * = 0,0006
M( i ) = D( i ) = 4
Результаты вычислений сведем в таблицу 3:
Таблица 3
| P( i ) | 0.018 | 0.036 | 0.192 | 0.102 | 0.029 | 0.0052 | 0.0006 |
| i | 0 | 1 | 4 | 6 | 8 | 10 | 12 |
По данным таблиц 1, 2, 3 построим графики огибающей вероятности для трех случаев: а) N>>V, б) N@V, в) N, V ® ¥ ; рис. 1.
Задание 2.
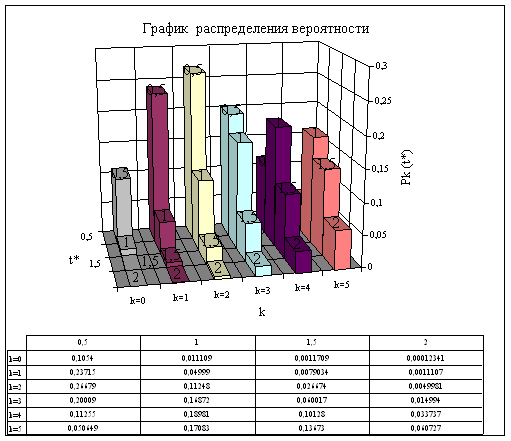
На коммутационную систему поступает простейший поток вызовов с интенсивностью А.
1. Рассчитать вероятность поступления не менее к вызовов за промежуток времени [ 0, t*]:
Рк(t*), где t* = 0,5; 1,0; 1,5; 2,0
2. Построить функцию распределения промежутков времени между двумя последовательными моментами поступления вызовов:
F(t*), t* = 0; 0,1; 0,2; …
3. Рассчитать вероятность поступления не менее к вызовов за интервал времени [ 0, t*]:
Pi³k(t*), где t* = 1
Примечание: 1. Для расчета значений A и V взять из задания 1.
2.Число вызовов к определить из выражения: к = [V/2] - целая часть числа.
3. Для построения графика взять не менее пяти значений F(t*). Результаты привести в виде таблицы:
| F(t*) | ||||
| t* |
4. Расчет Pi³k(t*) провести не менее чем для восьми членов суммы.
Решение:
Потоком вызовов называют последовательность однородных событий, поступающих через случайные интервалы времени. Поток вызовов может быть задан тремя эквивалентными способами:
1. Вероятностью поступления к вызовов за интервал времени [0,t).
2. Функцией распределения промежутков времени между двумя последовательными моментами поступления вызовов.
3. Вероятность поступления не менее к вызовов за интервал времени [0,t).
Свойства потоков: станционарность, ординарность и полное или частичное отсутствие последействия. Потоки классифицируются с точки зрения наличия или отсутствия этих свойств.
Основными характеристиками потоков вызовов являются: интенсивность m и параметр l.
Простейшим потоком называется ординарный стационарный поток без последействия.
Похожие работы
ость занятия которых подчиняется распределению Эрланга, соответственно равны: в) Распределение Пуассона используется при N, v → ∞ и имеет вид: где Y – средняя интенсивность нагрузки Y=a*v=0,45*9=4,05 Рисунок 3 Распределение Пуассона Математическое ожидание и дисперсия числа занятых линий, в бесконечном пучке линий равны между собой и вычисляются по формуле: Потоки ...
... работы необходимо начинать с приобретения методических руководств к курсовой работе Ниеталина Ж.Н. и Ниеталиной Ж.Ж. «Электрлiк байланыс теориясы» выпущенной в Алма-Ате в 1999 году, Ниеталина Ж.Н. и Ниеталиной Ж.Ж. «Теория электрической связи» учебное пособие к курсовой работе. Алма-Ата 2001г., а также учебное пособие Зюко А.Г. и др. «Теория передачи сигналов» – М.; «Связь» 1988г., «Теория ...
... такие стремления можно только с помощью государства. Неоклассическое направление интересует нас в том отношении, что сделанные в его русле теоретические выводы послужили полем для развития многих современных течений экономической мысли — монетаризма, неолиберализма и ряда теорий экономического роста. Название этого направления указывает на преемственность многих идей, выдвигавшихся классиками ...
... теории на новый мировоззренческий принцип - цивилизационный - сопровождался рядом важных процессов, которые в совокупности определили превращение научно-технологического прогресса в объект исследования экономической теории как науки. Все это обусловило важнейшее направление формирования новой методологии этой науки. Формационный подход опирался на производственные отношения, классы общества, ...

0 комментариев